Convergenza funzioni di variabili aleatorie
Sia Xn, n ≥ 1, una successione di v.a. i.i.d. con Xn ∼ Un(0,a), a > 0. Posto
Yn = $(Sn)/n=(X1+...+Xn)/n$ Studiare la convergenza di 1)Wn=$e^(Yn)$,per n$>=$1
2)$Zn =sqrtn(Yn −a/2)$,n$>=1$
1)Sapendo per la legge dei grandi numeri che Yn$rarr$ in d. a $a/2$, applico il teorema delle funzione continua per cui Xn$rarr$X allora g(Xn)$rarr$g(X). La soluzione è infatti che Wn$rarr$in d.,p.,q.c., a $e^(a/2)$.
2)Se il ragionamento precedente è giusto,la convergenza in distribuzione di Zn dovrebbe esssere Zn$rarr$in d. $sqrtn(a/2-a/2)=0$.
Nelle soluzioni mi dice invece che è sbagliato, e applicandomi il TLC arriva a tutt'altro risultato. Perchè? Essendo entrambe continue e funzioni di una v.a. i.i.d., perchè non posso risolvere entrambe nel 1) modo?
Yn = $(Sn)/n=(X1+...+Xn)/n$ Studiare la convergenza di 1)Wn=$e^(Yn)$,per n$>=$1
2)$Zn =sqrtn(Yn −a/2)$,n$>=1$
1)Sapendo per la legge dei grandi numeri che Yn$rarr$ in d. a $a/2$, applico il teorema delle funzione continua per cui Xn$rarr$X allora g(Xn)$rarr$g(X). La soluzione è infatti che Wn$rarr$in d.,p.,q.c., a $e^(a/2)$.
2)Se il ragionamento precedente è giusto,la convergenza in distribuzione di Zn dovrebbe esssere Zn$rarr$in d. $sqrtn(a/2-a/2)=0$.
Nelle soluzioni mi dice invece che è sbagliato, e applicandomi il TLC arriva a tutt'altro risultato. Perchè? Essendo entrambe continue e funzioni di una v.a. i.i.d., perchè non posso risolvere entrambe nel 1) modo?
Risposte
Il punto 1) è corretto anche se devi partire dalla convergenza più stretta per dedurne quella più lasca
Il ragionamento al punto 2) invece non lo è.
Le tue variabili iid $X_i$ sono tutte uniformi in $(0;a)$, quindi hai $mu=a/2$ e $sigma^2=a^2/12$
La tua variabile $Z_n$, scritta diversamente (ma nemmeno molto diversamente) è questa
$Z_n=(bar(X)_n-mu)sqrt(n)$
senza fare alcun conto, ma solo prendendo la DEFINIZIONE di TLC hai che
(ho preso un testo a caso eh
- clicca sull'immagine per ingrandirla)
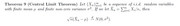
Quindi nel tuo caso, senza fare alcun conto, hai che
$(bar(X)_n-mu)sqrt(n)\stackrel(" "mathcal(L)" ")rarrN(0;a^2/12)$
Sì certo è possibile fare un ragionamento simile ma ti troveresti semmai con $oo xx 0$ e quindi non potresti concludere alcunché
Che non siamo nel medesimo caso del punto precedente lo puoi vedere anche scrivendo $Z_n$ in questo modo
$Z_n=(Sigmax)/sqrt(n)-sqrt(n)mu$
e non è mica vero che puoi applicare la Legge forte dei grandi numeri a $(Sigmax)/sqrt(n)$
Il ragionamento al punto 2) invece non lo è.
Le tue variabili iid $X_i$ sono tutte uniformi in $(0;a)$, quindi hai $mu=a/2$ e $sigma^2=a^2/12$
La tua variabile $Z_n$, scritta diversamente (ma nemmeno molto diversamente) è questa
$Z_n=(bar(X)_n-mu)sqrt(n)$
senza fare alcun conto, ma solo prendendo la DEFINIZIONE di TLC hai che
(ho preso un testo a caso eh
- clicca sull'immagine per ingrandirla)Quindi nel tuo caso, senza fare alcun conto, hai che
$(bar(X)_n-mu)sqrt(n)\stackrel(" "mathcal(L)" ")rarrN(0;a^2/12)$
"camicorte":
2)Se il ragionamento precedente è giusto,la convergenza in distribuzione di Zn dovrebbe esssere Zn$rarr$in d. $sqrtn(a/2-a/2)=0$.
Sì certo è possibile fare un ragionamento simile ma ti troveresti semmai con $oo xx 0$ e quindi non potresti concludere alcunché
Che non siamo nel medesimo caso del punto precedente lo puoi vedere anche scrivendo $Z_n$ in questo modo
$Z_n=(Sigmax)/sqrt(n)-sqrt(n)mu$
e non è mica vero che puoi applicare la Legge forte dei grandi numeri a $(Sigmax)/sqrt(n)$
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo