Aiuto ragionamento risoluzione esercizio v.a. gaussiane

[Marco Beta2]

Buongiorno e buona domanica a tutti Ho un esercizio che mi ha un attimo confuso e non so come procedere, vi scrivo la traccia di seguito e spero che qualcuno mi possa illuminare.

In un frigorifero sono conservate 5 provette sella sostanza A e 15 della sostanza B. La temperatura della sostanza A è modellata dalla v.a. gaussiana $T_A ~ N(0, 3)$ mentre quella della sostanza B è modellata da un'altra v.a. gaussiana $T_B ~ N(1, 2)$. Avendo misurato una temperatura minore di zero in una provetta scelta a caso, calcolare la probabilità di aver scelto la provetta con la sostanza A.

Sono partito col calcolarmi $P(A)=1/4$ e $P(B)=3/4$ poi, per quanto riguarda la probabilità di scelta in base alla temperatura, ho ipotizzato l'utilizzo della Q function però mi è venuto il dubbio sul come scrivere la temperatura minore di zero e stavo pensando di utilizzare una sua proprietà e cioè $1-Q((T_A - 0)/sqrt(3))$ ponendo $T_A=0$ ma non so se questo discorso sia effettivamente valido (cioè non so se quella scrittura mi descrive effettivamente una temperatura negativa) inoltre non ho capito quale sia il metodo per correlare la temperatura e la scelta di una provetta

Attendo vostre illuminazioni come sempre, grazie in anticipo

[ghira1]

"Marco Beta2":[quote="ghira"]
Parlami della distribuzione di $t_B$. Come mai con i miei poteri magici so che $P(t_B<0)<0,5$ solamente con le informazioni che tu mi hai dato?

Hai fatto questo discorso?

$Z=((0-1)/sqrt2)=-0.5$[/quote]

No. Anche perché non è vero.

Quant'è $P(t_B<1)$? Senza fare calcoli o cercare valori di $\Phi$ ecc.

[ghira1]

"Marco Beta2":
dovrei anche avere però $P(t<0|"Scelta la provetta A")=1/5$ cioè la probabilità che venga scelta A dato che aveva t<0 idem anche per la B con valore $1/15$

Anche $\frac{1}{5}$ e $\frac{1}{15}$ sono sbagliati ma questo lo sai che perché hai scritto i valori corretti altrove.

[Marco Beta2]

"ghira":

No. Anche perché non è vero.

Quant'è $P(t_B<1)$? Senza fare calcoli o cercare valori di $\Phi$ ecc.

Possiamo vederla come $P(t_B<0)=1-P(t_A<0)=1-0.5=0.5$?
Anche perchè la somma $P(t_B<0)+P(t_A<0)$ deve dare $1$ no?

[Lo_zio_Tom]

"Marco Beta2":
$P(t_B<1)=0$? Anche se la somma $P(t_B<0)+P(t_A<0)$ deve dare $1$

Se la media della gaussiana è 1 l'area a sinstra di 1 è $1/2$

...e perché quella somma dovrebbe dare 1? Sono due variabili indipendenti una dall'altra....

mi spiace dover sovrappormi a @ghira che ha tentato di instradarti in TUTTI i modi possibili...ma l'esercizio è di una banalità quasi disarmante....se non riesci a risolvere queste cose è il caso che tu faccia una pausa e ricominci a studiare bene (ma per bene eh) la teoria.
Ho capito che il tuo non è un esame di Statistica ma con queste lacune di certo non puoi andare avanti.

$P(T_a<0)=1/2$ (la media è zero e quindi l'area a sinistra di zero è ovviamente $1/2$)

$P(T_b<0)=Phi((0-1)/sqrt(2))=Phi(-0.707)=0.24$

$Phi$ significa "tabella della Gaussiana"...probabilmente non ce l'hai $-0.707$ allora guardi $0.707$ e ci metti la probabililtà complementare a quella della tabella





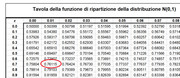
Infine, usi il teorema di Bayes

$P(A|T<0)=(1/4xx1/2)/(1/4xx1/2+3/4xx0.24)=41%$

$1/4$ e $3/4$ sono le probabilità di scegliere casualmente la provetta A (ce ne sono 5 su 20) oppure B (ce ne sono 15 su 20 totali)



scusa @ghira eh....è encomiabile il tuo impegno per farlo arrivare passo-passo alla soluzione ma dopo 3 pagine di 'sti commenti illeggibili non ho resistito

[ghira1]

"tommik":
scusa @ghira eh....è encomiabile il tuo impegno per farlo arrivare passo-passo alla soluzione ma dopo 3 pagine di 'sti commenti illeggibili non ho resistito

No, no. Va benissimo. Non sapevo più cosa dire, lo ammetto.