[Teoria dei Segnali] Interconnessione di sistemi

[djanthony931]

Salve, devo calcolare l'uscita complessiva del seguente sistema:



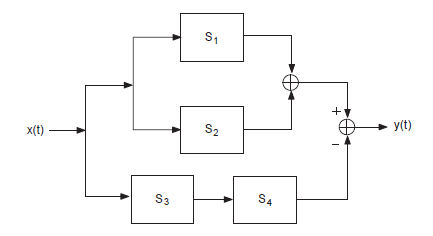
con:

$S_1: y(t)= 2x(t)+1$
$S_2: y(t)= sgn[x(t)]$
$S_3: y(t)= e^{x(t)}$
$S_4: y(t)= 2ln[|x(t)|]$

Non riesco a capire l'output della cascata $S_3 \rightarrow S_4$, sapete aiutarmi?

[pilloeffe]

Ciao djanthony93,

Sbaglierò, ma mi pare sia piuttosto semplice: l'output di $S_3$ è $y(t)= e^{x(t)}$ che costituisce l'input di $S_4$, per cui l'output di $S_4$ è $y(t)= 2ln[e^{x(t)}] = 2x(t)$

[djanthony931]

"pilloeffe":Ciao djanthony93,

Sbaglierò, ma mi pare sia piuttosto semplice: l'output di $S_3$ è $y(t)= e^{x(t)}$ che costituisce l'input di $S_4$, per cui l'output di $S_4$ è $y(t)= 2ln[e^{x(t)}] = 2x(t)$

Pensavo esattamente la stessa cosa, è quel modulo che mi frega

[pilloeffe]

Perché ti frega? Il modulo nell'argomento del logaritmo serve solo per essere sicuri che l'argomento sia positivo, ma nel caso di $e^{x(t)}$ è inutile perché sappiamo già che è positivo...