[Scienza delle Costruzioni]- Metodo Spostamenti
Buongiorno, devo risolvere questo esercizio con il metodo degli spostamenti con :
1) ipotesi aste rigide
2) ipotesi aste deformabili
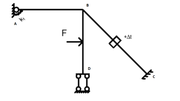
Come si deve considerare l'incastro cedevole (in termini di vettore delle incognite e nei vari schemi)? Non mi è mai capitato in altri esercizi ma so che potrebbe essere domanda d'orale.
1) ipotesi aste rigide
2) ipotesi aste deformabili

Come si deve considerare l'incastro cedevole (in termini di vettore delle incognite e nei vari schemi)? Non mi è mai capitato in altri esercizi ma so che potrebbe essere domanda d'orale.
Risposte
Il vettore delle incognite contiene gli spostamenti dei nodi, dunque non entra in gioco il cedimento. Invece lo andrai a considerare per la scrittura del vettore dei carichi \(\mathbf{F}^{(0)}\).
Cerco di spiegare il mio problema.
1) Hp: aste rigide. Calcolo la labilità della travatura associata \( l=2N-\mu -a=2*4-5-3=0 \)
Corretta? Ho considerato l'incastro cedevole come un normale incastro quindi passando alla travatura diventa una cerniera. Oppure, il fatto che sia un incastro cedevole, cambia qualcosa?
Se il calcolo è corretto, il sistema è a nodi fissi quindi considero il vettore delle incognite così fatto: \( \underline{u} = [\varphi B] \) . L'incastro cedevole allora verrà considerato sono nello schema 1 quando impongo la rotazione in B e considero l'asta AB deformata.
2) Hp aste deformabili. In questo caso \( \underline{u} = \( [A,uxB,uyB,\varphi B,uxD] \)
Ho messo A generico perchè solitamente quando abbiamo un incastro vincolato esternamente non lo consideriamo nel vettore u (già gli spostamenti sono bloccati) ma in questo caso essendo cedevole immagino cambierà qualcosa nel vettore... Come ne teniamo conto?
Nei vari schemi, dove imponiamo uno spostamento unitario, non cambia nulla: continuo a considerare quell'asta AB vincolata allo stesso modo (anche se non so i valori).
P.s. Per quanto riguarda il vettore \( F0 \) =0 in entrambi i casi visto che non abbiamo forze applicate ai nodi.
Invece \( R0 \) per L'(Hp1) in A " non succede nulla" se devo considerare solo \( \varphi B \)
per L' (Hp2) in A "non succede nulla" visto che il carico è applicato in DB
1) Hp: aste rigide. Calcolo la labilità della travatura associata \( l=2N-\mu -a=2*4-5-3=0 \)
Corretta? Ho considerato l'incastro cedevole come un normale incastro quindi passando alla travatura diventa una cerniera. Oppure, il fatto che sia un incastro cedevole, cambia qualcosa?
Se il calcolo è corretto, il sistema è a nodi fissi quindi considero il vettore delle incognite così fatto: \( \underline{u} = [\varphi B] \) . L'incastro cedevole allora verrà considerato sono nello schema 1 quando impongo la rotazione in B e considero l'asta AB deformata.
2) Hp aste deformabili. In questo caso \( \underline{u} = \( [A,uxB,uyB,\varphi B,uxD] \)
Ho messo A generico perchè solitamente quando abbiamo un incastro vincolato esternamente non lo consideriamo nel vettore u (già gli spostamenti sono bloccati) ma in questo caso essendo cedevole immagino cambierà qualcosa nel vettore... Come ne teniamo conto?
Nei vari schemi, dove imponiamo uno spostamento unitario, non cambia nulla: continuo a considerare quell'asta AB vincolata allo stesso modo (anche se non so i valori).
P.s. Per quanto riguarda il vettore \( F0 \) =0 in entrambi i casi visto che non abbiamo forze applicate ai nodi.
Invece \( R0 \) per L'(Hp1) in A " non succede nulla" se devo considerare solo \( \varphi B \)
per L' (Hp2) in A "non succede nulla" visto che il carico è applicato in DB


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo