Ponte - Calcolo spostamento
Salve a tutti,
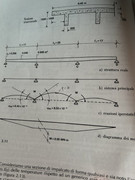
ho una curiosità. Nelle immagini allegati è presente una trave a 3 campate, in particolare nella prima campata per calcolare la rotazione si utilizza una struttura ausiliaria, come illustrata nell'altra immagine, in cui la trave appoggiata-appoggiata diventa una mensola, viene calcolato lo spostamento all'estremità. Alla fine la rotazione della trave originale viene calcolata come lo spostamento di prima diviso la lunghezza della trave
Che tipo di metodo è stato utilizzato?

ho una curiosità. Nelle immagini allegati è presente una trave a 3 campate, in particolare nella prima campata per calcolare la rotazione si utilizza una struttura ausiliaria, come illustrata nell'altra immagine, in cui la trave appoggiata-appoggiata diventa una mensola, viene calcolato lo spostamento all'estremità. Alla fine la rotazione della trave originale viene calcolata come lo spostamento di prima diviso la lunghezza della trave
Che tipo di metodo è stato utilizzato?


Risposte
Le immagini caricate risultano a bassa risoluzione (240x320) per cui non si capisce nulla.
Cliccando sopra ora si vede?
SI 
Non sono sicuro di poterti rispondere, ma ci guardo.

Non sono sicuro di poterti rispondere, ma ci guardo.
Se capisco bene si tratta di un problema di variazione di temperatura lungo la sezione.
Ora dovrei studiarci di più, perchè siamo nel caso di h=h(x), ma almeno nel caso semplice di h = costante la giustificazione è la seguente (tralasciamo qualunque discorso sui segni, facciamo riferimento alla seconda pagina e prendiamo gli assi da destra a sinistra):
per la trave incastrata lo spostamento per $x=l_1$ vale:
$v_A = v(l) = (alpha*Delta T)/(2h) * l_1^2$
mentre per la trave appoggiata la rotazione per $x=0$ vale:
$phi_B = phi(0) = (alpha*Delta T)/(2h) * l_1$
per cui effettivamente
$phi_B = v_A/l_1$
In pratica nel testo si ammette che tale relazione valga anche per h=h(x). Il vantaggio credo che consista nel fatto che la trave incastrata a sbalzo ammette delle condizioni al contorno (spostamento e rotazione nulli per x=0) che sono più semplici di quelle della trave appoggiata.
Non so se ti sono stato di vero aiuto, ma se trovo altro lo aggiungo al post.
Ora dovrei studiarci di più, perchè siamo nel caso di h=h(x), ma almeno nel caso semplice di h = costante la giustificazione è la seguente (tralasciamo qualunque discorso sui segni, facciamo riferimento alla seconda pagina e prendiamo gli assi da destra a sinistra):
per la trave incastrata lo spostamento per $x=l_1$ vale:
$v_A = v(l) = (alpha*Delta T)/(2h) * l_1^2$
mentre per la trave appoggiata la rotazione per $x=0$ vale:
$phi_B = phi(0) = (alpha*Delta T)/(2h) * l_1$
per cui effettivamente
$phi_B = v_A/l_1$
In pratica nel testo si ammette che tale relazione valga anche per h=h(x). Il vantaggio credo che consista nel fatto che la trave incastrata a sbalzo ammette delle condizioni al contorno (spostamento e rotazione nulli per x=0) che sono più semplici di quelle della trave appoggiata.
Non so se ti sono stato di vero aiuto, ma se trovo altro lo aggiungo al post.
Grazie per la risposta, mi trovo con la tua considerazione. Ma perché il testo fa prima riferimento alla trave incastrata e non direttamente all’appoggio-appoggio? Questo era il mio cruccio


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo