[Elettrotecnica] Analisi circuito nel dominio del tempo
Salve a tutti. Sono alle "prime armi" con lo studio dell'elettrotecnica. Ho alcune difficoltà nello studio dei circuiti in regime temporale. Ad esempio questo
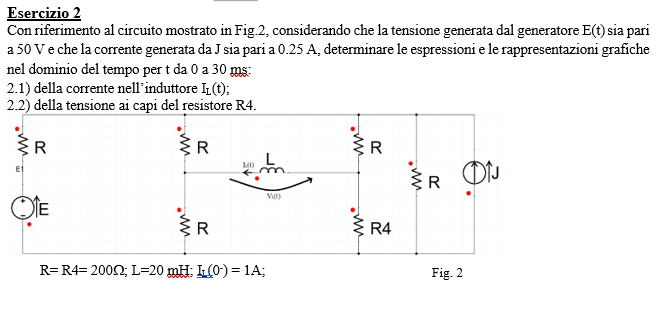
Ho provato a semplificare le resistenze per semplificare il circuito o applicare Thevenin ma senza risultato, forse sono completamente fuori strada
Se qualcuno può darmi una mano, anche spiegando l'approccio da seguire per la risoluzione di questo tipo di circuiti ne sarei grato, grazie!

Ho provato a semplificare le resistenze per semplificare il circuito o applicare Thevenin ma senza risultato, forse sono completamente fuori strada
Se qualcuno può darmi una mano, anche spiegando l'approccio da seguire per la risoluzione di questo tipo di circuiti ne sarei grato, grazie!
Risposte
Puoi farci vedere come hai cercato di ricavare il circuito equivalente di Thevenin, "visto" dall'induttore?
BTW Cosa starebbero a indicare quei punti rossi?
Ti do un primo suggerimento: per risolvere basta semplicemente usare la "simmetria" circuitale.
BTW Cosa starebbero a indicare quei punti rossi?
Ti do un primo suggerimento: per risolvere basta semplicemente usare la "simmetria" circuitale.
Grazie, riprovo
Ho provato prima a semplificare le resistenze
Le 3 a sinistra, hanno resistenza equivalente R' (200+200+200)
Le 3 a destra R'' 133,33 (200+200 // 200)
Poi ho analizzato il circuito un "generatore per volta" e ho sommato i risultati
Le 3 a sinistra, hanno resistenza equivalente R' (200+200+200)
Le 3 a destra R'' 133,33 (200+200 // 200)
Poi ho analizzato il circuito un "generatore per volta" e ho sommato i risultati
... e quei punti rossi ? 
Non credo abbiamo significato 
Ho convertito il gic in uno di tensione in modo che il circuito sia simmetrico (la tensione risulta uguale al generatore di sinistra), ho cercato di applicare il principio di sovrap. degli effetti ma non riesco a calcolarmi le resistenze equivalenti e di conseguenza la corrente
Ho convertito il gic in uno di tensione in modo che il circuito sia simmetrico (la tensione risulta uguale al generatore di sinistra), ho cercato di applicare il principio di sovrap. degli effetti ma non riesco a calcolarmi le resistenze equivalenti e di conseguenza la corrente
Per risondere alla prima domanda, andando a ricavarti il circuito equivalente "visto" dall'induttore, ti basta osservare che, essendo i quattro resistori centrali della rete di pari valore R, qualunque tensione venga ad esserci fra il nodo (conduttore orizzontale) superiore ed inferiore della rete, la tensione fra i punti (diciamo A e B) di collegamento dell'induttore sarà nulla e quindi
$E_{Th}=V_{AB0}=0\ \text{V}$,
indipendente dal valore dei generatori.
Per la resistenza equivalente, si può poi bypassare qualsiasi semplificazione semplicemente notando che la rete resistiva ottenuta, una volta passivata la rete, per la simmetria, sarà semplicemente
$R_{Th}=R$,
di conseguenza, la corrente nell'induttore presenterà una semplice discesa esponenziale, a partire dal valore iniziale verso lo zero, con costante di tempo \( \tau=L/R\).
$E_{Th}=V_{AB0}=0\ \text{V}$,
indipendente dal valore dei generatori.
Per la resistenza equivalente, si può poi bypassare qualsiasi semplificazione semplicemente notando che la rete resistiva ottenuta, una volta passivata la rete, per la simmetria, sarà semplicemente
$R_{Th}=R$,
di conseguenza, la corrente nell'induttore presenterà una semplice discesa esponenziale, a partire dal valore iniziale verso lo zero, con costante di tempo \( \tau=L/R\).
Grazie mille, ho capito il ragionamento riguardo la tensione.
Non riesco a capire però perchè data la simmetria delle resistenze, quella equivalente vale R
Non riesco a capire però perchè data la simmetria delle resistenze, quella equivalente vale R
Semplicemente perché, passivata la rete, fatto il parallelo fra i resistori esterni, portati (anche se non necessario) all'esterno i punti A e B, avrai la seguente configurazione resistiva
[fcd="fig.1"][FIDOCAD]
FJC C 1.5
FJC A 0.3
FJC B 0.3
MC 230 55 1 0 ey_libraries.pasres0
MC 230 80 1 0 ey_libraries.pasres0
LI 230 70 235 70 0
LI 230 65 230 75 0
MC 240 70 2 0 ey_libraries.refpnt1
TY 235 79 4 3 0 0 0 Arial R
TY 235 55 4 3 0 0 0 Arial R
MC 210 66 1 0 ey_libraries.pasres0
MC 190 55 1 1 ey_libraries.pasres0
MC 190 80 1 1 ey_libraries.pasres0
LI 190 70 185 70 0
LI 190 65 190 75 0
MC 180 70 2 1 ey_libraries.refpnt1
TY 181 80 4 3 0 0 0 Arial R
TY 181 54 4 3 0 0 0 Arial R
LI 190 50 230 50 0
LI 210 61 210 50 0
LI 190 90 230 90 0
LI 210 76 210 90 0
TY 214 67 4 3 0 0 0 Arial R/2
TY 243 67 4 3 0 0 0 * A
TY 174 66 4 3 0 0 0 * B[/fcd]
dalla quale, senza scomodare la trasformazione triangolo-stella, ricordando che in generale per ottenere la resistenza equivalente si va a forzare con un GIT o con un GIC la tensione o la corrente (applicata o entrante) nel bipolo, per poi ottenere la Req dal rapporto fra tensione e corrente erogata dal generatore, è evidente che, per la simmetria della rete, il resistore R/2 sarà influente in quanto sottoposto ad una differenza di potenziale nulla; ne segue che
$R_{eq}=(R+R)/2=R$
La simmetria, quando presente (e applicabile), ti fornisce un'arma risolutiva potentissima, basta pensare al classico cubo resistivo (come anche a tutti gli altri solidi platonici).
[fcd="fig.1"][FIDOCAD]
FJC C 1.5
FJC A 0.3
FJC B 0.3
MC 230 55 1 0 ey_libraries.pasres0
MC 230 80 1 0 ey_libraries.pasres0
LI 230 70 235 70 0
LI 230 65 230 75 0
MC 240 70 2 0 ey_libraries.refpnt1
TY 235 79 4 3 0 0 0 Arial R
TY 235 55 4 3 0 0 0 Arial R
MC 210 66 1 0 ey_libraries.pasres0
MC 190 55 1 1 ey_libraries.pasres0
MC 190 80 1 1 ey_libraries.pasres0
LI 190 70 185 70 0
LI 190 65 190 75 0
MC 180 70 2 1 ey_libraries.refpnt1
TY 181 80 4 3 0 0 0 Arial R
TY 181 54 4 3 0 0 0 Arial R
LI 190 50 230 50 0
LI 210 61 210 50 0
LI 190 90 230 90 0
LI 210 76 210 90 0
TY 214 67 4 3 0 0 0 Arial R/2
TY 243 67 4 3 0 0 0 * A
TY 174 66 4 3 0 0 0 * B[/fcd]
dalla quale, senza scomodare la trasformazione triangolo-stella, ricordando che in generale per ottenere la resistenza equivalente si va a forzare con un GIT o con un GIC la tensione o la corrente (applicata o entrante) nel bipolo, per poi ottenere la Req dal rapporto fra tensione e corrente erogata dal generatore, è evidente che, per la simmetria della rete, il resistore R/2 sarà influente in quanto sottoposto ad una differenza di potenziale nulla; ne segue che
$R_{eq}=(R+R)/2=R$
La simmetria, quando presente (e applicabile), ti fornisce un'arma risolutiva potentissima, basta pensare al classico cubo resistivo (come anche a tutti gli altri solidi platonici).

Ok grazie mille, ora è chiaro 
E ora tocca alla tensione su R4; come pensi di fare?
Pensavo di applicare semplicemente Kirchhoff alla maglia di destra, calcolando la corrente entrante in r4 e moltiplicando per il valore della resistenza.
Sia così che applicando ad esempio milmann mi da lo stesso valore finale, cioè 16,6 V
Ma a quanto pare la sto facendo troppo facile
Update: In questo modo però non sto considerando la corrente sull'induttore. Però questo valore dovrebbe essere quello finale, quando la corrente che scorre sull'ind. è pari a zero. O sbaglio?
Sia così che applicando ad esempio milmann mi da lo stesso valore finale, cioè 16,6 V
Ma a quanto pare la sto facendo troppo facile
Update: In questo modo però non sto considerando la corrente sull'induttore. Però questo valore dovrebbe essere quello finale, quando la corrente che scorre sull'ind. è pari a zero. O sbaglio?
Non sbagli, a quel valore devi aggiungere il contributo della corrente nell'induttore, che chiaramente sarà iL(t)/2, verso l'alto, in R4.
Quindi
$v_4(t)=16.6-R_4(i_L(t))/2$
Quindi
$v_4(t)=16.6-R_4(i_L(t))/2$
"Batixono":
Ho provato prima a semplificare le resistenze
Le 3 a sinistra, hanno resistenza equivalente R' (200+200+200)
Le 3 a destra R'' 133,33 (200+200 // 200)
Poi ho analizzato il circuito un "generatore per volta" e ho sommato i risultati
Ho fatto questo passaggio in foto, che però non credo sia giusto
Questo messaggio non lo avevo visto, ma schemi e calcoli sono tutti errati.
"RenzoDF":
Questo messaggio non lo avevo visto, ma schemi e calcoli sono tutti errati.
Sisi questo era un primo calcolo che ho capito subito essere sbagliato
Grazie mille ancora dell'aiuto!
Di nulla.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo