[Dinamica dei sistemi] Esercizio su generatore di vapore, dominio tempo
Salve,
mi sono imbattuto in questo esercizio di dinamica e controllo. L'argomento è "analisi del sistema nel dominio tempo".
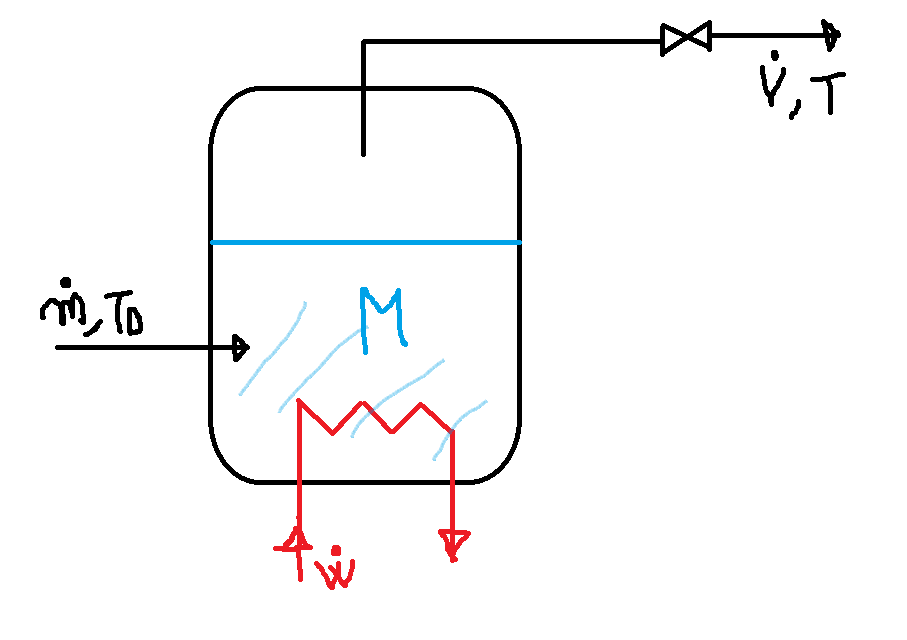
Si ha il generatore di vapore rappresentato in Figura. Si possono fare le seguenti ipotesi:
- La temperatura di alimentazione dell'acqua è costante a $T_0=320 K$, ma la sua portata $\dot{m}$ può variare (è un disturbo).
- il calore specifico dell’acqua può essere considerato costante e pari a 4.2 kJ/(kg · K); il calore latente di evaporazione dell’acqua può essere considerato costante e pari a λ = 2100 kJ/kg.
- la massa di vapore all’interno dell’evaporatore è trascurabile rispetto alla massa di liquido (M);
- la potenza termica fornita all’evaporatore \dot{W} e la portata di uscita di vapore \dot{V} possono essere variati dal sistema di controllo (sono variabili manipolate).
I dati nominali sono: $\dot{m}=180 \: kg/s$, $M=16200 \: kg$, $T=493K$.
Si chiede di:
1) Determinare il valore nominale della potenza termica, $\dot{W}$, da fornire al generatore.
2) Scrivere le equazioni dinamiche di bilancio di materia e di energia che permettono di ottenere l’andamento della temperatura T e della massa (di liquido) M all’interno del generatore.
3) Discutere analiticamente quale tipo di dinamica (ad esempio prim’ordine, con ritardo, etc.) ci si attende per M e T a fronte di variazioni degli ingressi.
Premetto che i miei dubbi sorgono sui punti 2 e 3. Per il primo, me la sono sbrigata impostando un bilancio di energia in condizioni nominali (stazionarie):
$\dot{W}=C_p(T-T_0) \dot{m} + \lambda \dot{V} $
Dove, da un bilancio di materia si vede che $\dot{V}=\dot{m}$ (nominale).
Per l'equazione dinamica del bilancio di materia ho scritto:
$ \dot{m} - \dot{V}=dM/dt $
E per quella di energia:
$ MC_p\dfrac{dT}{dt}=\dot{m}C_p(T-T_0)+\lambda \dot{V} + \dot{W} $
Per l'ultima equazione, quella della energia, non sono sicuro dei segni. Infine, per il punto (3) non saprei come muovermi. Visto che la soluzione non è determinabile analiticamente. L'unica idea che mi viene in mente è quella di manipolare le equazioni differenziali, tramite derivazioni e sostituzioni, per arrivare ad un'unica equazione differenziale di un certo ordine. Ma non saprei come fare nel modo giusto.
Qualcuno ha qualche idea? Grazie per l'attenzione!
mi sono imbattuto in questo esercizio di dinamica e controllo. L'argomento è "analisi del sistema nel dominio tempo".
Si ha il generatore di vapore rappresentato in Figura. Si possono fare le seguenti ipotesi:
- La temperatura di alimentazione dell'acqua è costante a $T_0=320 K$, ma la sua portata $\dot{m}$ può variare (è un disturbo).
- il calore specifico dell’acqua può essere considerato costante e pari a 4.2 kJ/(kg · K); il calore latente di evaporazione dell’acqua può essere considerato costante e pari a λ = 2100 kJ/kg.
- la massa di vapore all’interno dell’evaporatore è trascurabile rispetto alla massa di liquido (M);
- la potenza termica fornita all’evaporatore \dot{W} e la portata di uscita di vapore \dot{V} possono essere variati dal sistema di controllo (sono variabili manipolate).
I dati nominali sono: $\dot{m}=180 \: kg/s$, $M=16200 \: kg$, $T=493K$.

Si chiede di:
1) Determinare il valore nominale della potenza termica, $\dot{W}$, da fornire al generatore.
2) Scrivere le equazioni dinamiche di bilancio di materia e di energia che permettono di ottenere l’andamento della temperatura T e della massa (di liquido) M all’interno del generatore.
3) Discutere analiticamente quale tipo di dinamica (ad esempio prim’ordine, con ritardo, etc.) ci si attende per M e T a fronte di variazioni degli ingressi.
Premetto che i miei dubbi sorgono sui punti 2 e 3. Per il primo, me la sono sbrigata impostando un bilancio di energia in condizioni nominali (stazionarie):
$\dot{W}=C_p(T-T_0) \dot{m} + \lambda \dot{V} $
Dove, da un bilancio di materia si vede che $\dot{V}=\dot{m}$ (nominale).
Per l'equazione dinamica del bilancio di materia ho scritto:
$ \dot{m} - \dot{V}=dM/dt $
E per quella di energia:
$ MC_p\dfrac{dT}{dt}=\dot{m}C_p(T-T_0)+\lambda \dot{V} + \dot{W} $
Per l'ultima equazione, quella della energia, non sono sicuro dei segni. Infine, per il punto (3) non saprei come muovermi. Visto che la soluzione non è determinabile analiticamente. L'unica idea che mi viene in mente è quella di manipolare le equazioni differenziali, tramite derivazioni e sostituzioni, per arrivare ad un'unica equazione differenziale di un certo ordine. Ma non saprei come fare nel modo giusto.
Qualcuno ha qualche idea? Grazie per l'attenzione!
Risposte
I segni nell'equazione dell'energia non sono corretti. I primi due termini a destra devono essere negativi (si tratta di calore in uscita e non in ingresso al sistema)
Così facendo in condizioni stazionarie (derivata nulla) l'equazione si riconduce alla prima equazione che hai scritto.
Quanto alla dinamica, chiaramente, nell'ambito delle approssimazioni del modello, la massa M è un integratore puro.
Per l'energia invece se supponiamo
a) piccole variazioni attorno ad un punto di equilibrio contraddistinto da M=Mo e ovviamente portata vapore = portata acqua=q=costante, temperatura di regime tale da soddisfare l'equazione di bilancio in condizioni stazionarie e tutte le derivate nulle, oppure
b) la presenza di un regolatore di livello perfetto tale da assicurare in ogni momento M=Mo e inoltre portata acqua=q=costante
allora si vede abbastanza facilmente che la dinamica della temperatura è contraddistinta da una costante di tempo
Così facendo in condizioni stazionarie (derivata nulla) l'equazione si riconduce alla prima equazione che hai scritto.
Quanto alla dinamica, chiaramente, nell'ambito delle approssimazioni del modello, la massa M è un integratore puro.
Per l'energia invece se supponiamo
a) piccole variazioni attorno ad un punto di equilibrio contraddistinto da M=Mo e ovviamente portata vapore = portata acqua=q=costante, temperatura di regime tale da soddisfare l'equazione di bilancio in condizioni stazionarie e tutte le derivate nulle, oppure
b) la presenza di un regolatore di livello perfetto tale da assicurare in ogni momento M=Mo e inoltre portata acqua=q=costante
allora si vede abbastanza facilmente che la dinamica della temperatura è contraddistinta da una costante di tempo
[math]\tau=\frac{M_0}{q}[/math]
Grazie mille Ingres, scusa se ti rispondo solo adesso ma ero in vacanza e mi è passato di mente! Tutto ciò che hai scritto mi torna e, quindi, da quanto ho capito la dinamica della temperatura è del primo ordine, dico bene?
Perché anche se M varia nel tempo (in un modo che dipende da come variano m e V), l'equazione differenziale dell'energia rimane del primo ordine in quanto cambia solo la forzante.
Saluti
Perché anche se M varia nel tempo (in un modo che dipende da come variano m e V), l'equazione differenziale dell'energia rimane del primo ordine in quanto cambia solo la forzante.
Saluti
Si. Corretto.
Ovviamente è un'approssimazione considerare un sistema con una costante di tempo variabile con le condizioni operative, rispetto alla realtà di un sistema non lineare.
Ma questa approssimazione è giustificata dal fatto che, normalmente, i sistemi lavorano entro entro certi range di funzionamento e con transitori molto controllati per cui, in molti casi, le variazioni sono abbastanza ridotte e lente da rendere tecnicamente accettabile questa assunzione.
Inoltre questo modo di procedere permette di operare con i classici strumenti della teoria dei sistemi lineari, purché si tenga conto che alcuni parametri possono avere una certa variabilità.
Ovviamente è un'approssimazione considerare un sistema con una costante di tempo variabile con le condizioni operative, rispetto alla realtà di un sistema non lineare.
Ma questa approssimazione è giustificata dal fatto che, normalmente, i sistemi lavorano entro entro certi range di funzionamento e con transitori molto controllati per cui, in molti casi, le variazioni sono abbastanza ridotte e lente da rendere tecnicamente accettabile questa assunzione.
Inoltre questo modo di procedere permette di operare con i classici strumenti della teoria dei sistemi lineari, purché si tenga conto che alcuni parametri possono avere una certa variabilità.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo