Chiarimento su diagramma Bode in modo "preciso"

[rocco.g1]

Ciao a tutti!

Spero mi sappiate aiutare...
il mio prof vuole che i diagrammi di bode si facciano in modo preciso... diversamente da come ero abituatoa farli io...

vi spiego... in genere, per quanto riguarda le ampiezze, io disegno il diagramma ed indico le varie pendenze di volta in volta...e mi fermo li...

lui invece fa altri calcoli... che però non riesco a comprendere...

Ad esempio, ha fatto questo esercizio:

$H(s)=125 * [(s(s+20)(s+40))/((s+1)(s+10))]$

il diagramma se lo faccio mi esce uguale al suo, solo che lui ha aggiunto altri dati...

vi riporto qui il diagramma:



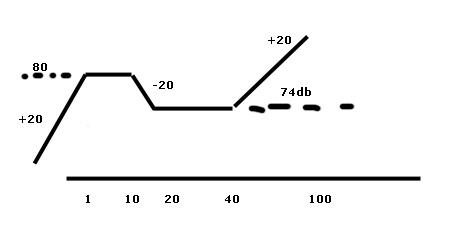
Non riesco a capire come si sia calcolato quel 80db e quel 74db...

lui poi ha scritto queste così qui:

$H(s) = (10^4)s$ per |s| << 1 => $|H(j1)| = 10^4 = 80db$

poi ha scritto ancora:
0,3 decadi w=20db/sec -> dinamica 20*0,3 = 6db

mi aiutate a capire che ha fatto?
sul mio libro non ci sono queste formule e non capisco quindi come si ricavino... cioè non so fare i passaggi intermedi e soprattutto non ne capisco il motivo...
Spero mi sappiate aiutare...

Grazie!

[_luca.barletta]

noti che in un intorno di $omega=1$ il diagramma è costante, quindi calcola il valore assunto dalla $|H(jomega)|$ in quel punto

[_luca.barletta]

poi, da $omega=10$ a $omega=20$ cadono 0.3 decadi; in questo intervallo la |H(jomega)| decade di 20 dB/dec, quindi...

[rocco.g1]

"luca.barletta":poi, da $omega=10$ a $omega=20$ cadono 0.3 decadi; in questo intervallo la |H(jomega)| decade di 20 dB/dec, quindi...

il tuo primo post l'ho capito... quindi devo fare la stessa cosa tra 20 e 40 perchè anche lì è costante, giusto?

non ho capito però la storia delle 0.3 decadi... come si fanno a calcolare?

[_luca.barletta]

$log_(10)20-log_(10)10=0.3$

[rocco.g1]

ok, ottimo!


ho provato a calcolare $|H(1j)|$ ma non mi viene 10^4, mi viene qualcosa intorno a 7000, non devo solo sostituire j1 nella funzione di trasferimento, dividere parte reale e immaginare, sommare i due al quadrato e poi fare la radice?

[_luca.barletta]

"rocco.g": non devo solo sostituire j1 nella funzione di trasferimento, dividere parte reale e immaginare, sommare i due al quadrato e poi fare la radice?

certo, ma in $omega=1$ non raggiungerai proprio il max locale che assume la $|H(jomega)|$, perchè in $|omega|=1$ hai proprio un polo (avresti un raccordo della $|H(jomega)|$ in quel punto). Dovresti andare un po' più 'a destra' di $omega=1$

[rocco.g1]

e quindi devo fare a caso? cioè... perchè a lui esce proprio esattamente quasi 10^4 ?

[rocco.g1]

è da ieri che ci provo... lui scrive proprio (j1) e se lo calcola... ma a lui esce 10^4 ed a me no...

eppure i calcoli son quelli... che cosa è che sbaglio?

[rocco.g1]

ok, mi son messo con calma ed ho capito tutto...

bisogna studiare la funzione di trasferimento per s che tende quasi a zero... ma non a zero proprio...
quindi è un limite, se vogliamo...
poi si trasforma il risultato in decibel...

tutto ok...

thanks!