Problema di combinatoria
Ho questo problemino: generare tutti i sottoinsiemi di un insieme dato, ordinato per dimensione.
Per esempio: {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}.
Il problema in questo caso non è tanto l'implementazione dell'algoritmo, ma capire come ottenere l'algoritmo. Devo implementare qualcosa relativo al calcolo combinatorio per risolverlo?
Potreste darmi una pista su cui ragionare?
Per esempio: {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}.
Il problema in questo caso non è tanto l'implementazione dell'algoritmo, ma capire come ottenere l'algoritmo. Devo implementare qualcosa relativo al calcolo combinatorio per risolverlo?
Potreste darmi una pista su cui ragionare?
Risposte
sono: {0,1,2} {0,1,3} {0,1,4} {0,2,3} {0,2,4} {0,3,4} {1,2,3} {1,2,4} {1,3,4} {2,3,4}.
Bene, ora data una di queste combinazioni (e considerando noti anche i parametri $n$ e $k$), bisogna stabilire se tale combinazione è l'ultima oppure no (e in tal caso bisogna ovviamente anche determinare quella successiva).
Assumiamo che gli elementi della generica combinazione siano individuati da un indice $i$ che parte da $0$ (un po' come avviene con gli array).
L'ultima combinazione può essere vista come quella in cui i singoli elementi che la costituiscono hanno tutti raggiunto un valore $MAX(i)=n-k+i$.
Magari la seguente schematizzazione può essere utile:
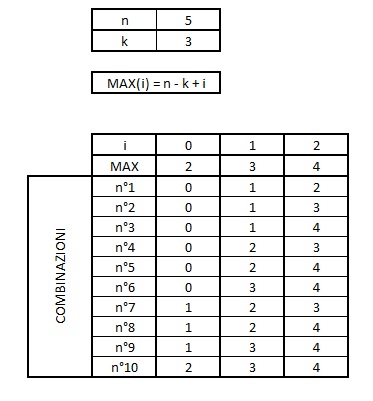
Quindi la funzione next_combination() andrà ad analizzare la combinazione corrente iniziando dall'ultimo elemento, se esso è minore del relativo massimo allora sarà incrementato di $1$, altrimenti si passerà all'elemento precedente... il resto è facile da intuire.
Assumiamo che gli elementi della generica combinazione siano individuati da un indice $i$ che parte da $0$ (un po' come avviene con gli array).
L'ultima combinazione può essere vista come quella in cui i singoli elementi che la costituiscono hanno tutti raggiunto un valore $MAX(i)=n-k+i$.
Magari la seguente schematizzazione può essere utile:

Quindi la funzione next_combination() andrà ad analizzare la combinazione corrente iniziando dall'ultimo elemento, se esso è minore del relativo massimo allora sarà incrementato di $1$, altrimenti si passerà all'elemento precedente... il resto è facile da intuire.
Ma in questo caso la i varia da 0 a 2 perchè k=3, ma k nel frattempo deve variare da 1 a 3. Quindi il massimo elemento di ogni combinazione va calcolato prima di eseguire il ciclo. Poi però non ho ben capito cosa avviene nel main. Perchè c'è un vettore di char e non capisco questo $v[u]$.
Cerco di spiegarmi meglio.
Dimentica per il momento quello che era il tuo intento iniziale (poi verrà da sé), e ipotizziamo di voler risolvere il seguente esercizio: stampare a schermo tutte le combinazioni semplici delle prime $5$ lettere dell'alfabeto prese $3$ alla volta.
Sarà ovviamente $n=5$ e $k=3$. Dichiariamo un array $v$ contenente il nostro set di elementi:
Riprendiamo ora le e combinazioni semplici in base $3$ dell'insieme ${0, 1, 2, 3, 4}$ che ti ho chiesto in precedenza e ipotizziamo di salvarle in $10$ array di $k=3$ elementi ciascuno:
Come conseguenza avremo che:
Dove l'ultima colonna restituisce appunto quello che stavamo cercando, ossia le combinazioni semplici delle prime $5$ lettere dell'alfabeto prese $3$ alla volta. La prima colonna dovrebbe invece chiarirti il significato di quel $v[u]$ di un mio precedente post.
A questo punto risulta evidente che il tutto si riduce ad escogitare un modo per ottenere in modo automatico gli array $u_1,u_2,...,u_9,u_10$.
Ed è qui che entra in gioco la funzione:
Essa:
- per $u={0,1,2}$ restituirà true e modificherà il suddetto array in $u={0,1,3}$;
- per $u={0,1,3}$ restituirà true e modificherà il suddetto array in $u={0,1,4}$;
...
- per $u={1,3,4}$ restituirà true e modificherà il suddetto array in $u={2,3,4}$;
- per $u={2,3,4}$ restituirà false.
Quindi per risolvere l'esercizio che ho proposto all'inizio di questo messaggio, non resta altro che implementare la funzione next_combination() utilizzando i suggerimenti che ti ho dato nel precedente post. Inizia a buttare giù qualche riga di codice, poi nel caso possiamo ragionarci insieme.
Dimentica per il momento quello che era il tuo intento iniziale (poi verrà da sé), e ipotizziamo di voler risolvere il seguente esercizio: stampare a schermo tutte le combinazioni semplici delle prime $5$ lettere dell'alfabeto prese $3$ alla volta.
Sarà ovviamente $n=5$ e $k=3$. Dichiariamo un array $v$ contenente il nostro set di elementi:
char v[n] = {a, b, c, d, e};Riprendiamo ora le e combinazioni semplici in base $3$ dell'insieme ${0, 1, 2, 3, 4}$ che ti ho chiesto in precedenza e ipotizziamo di salvarle in $10$ array di $k=3$ elementi ciascuno:
unsigned int u_1[k] = {0,1,2};
unsigned int u_2[k] = {0,1,3};
unsigned int u_3[k] = {0,1,4};
unsigned int u_4[k] = {0,2,3};
unsigned int u_5[k] = {0,2,4};
unsigned int u_6[k] = {0,3,4};
unsigned int u_7[k] = {1,2,3};
unsigned int u_8[k] = {1,2,4};
unsigned int u_9[k] = {1,3,4};
unsigned int u_10[k] = {2,3,4};Come conseguenza avremo che:
{v[u_1[0]], v[u_1[1]], v[u_1[2]]} ≡ {v[0], v[1], v[2]} ≡ {a, b, c}
{v[u_2[0]], v[u_2[1]], v[u_2[2]]} ≡ {v[0], v[1], v[3]} ≡ {a, b, d}
{v[u_3[0]], v[u_3[1]], v[u_3[2]]} ≡ {v[0], v[1], v[4]} ≡ {a, b, e}
...
{v[u_8[0]], v[u_8[1]], v[u_8[2]]} ≡ {v[1], v[2], v[4]} ≡ {b, c, e}
{v[u_9[0]], v[u_9[1]], v[u_9[2]]} ≡ {v[1], v[3], v[4]} ≡ {b, d, e}
{v[u_10[0]], v[u_10[1]], v[u_10[2]]} ≡ {v[2], v[3], v[4]} ≡ {c, d, e}Dove l'ultima colonna restituisce appunto quello che stavamo cercando, ossia le combinazioni semplici delle prime $5$ lettere dell'alfabeto prese $3$ alla volta. La prima colonna dovrebbe invece chiarirti il significato di quel $v[u]$ di un mio precedente post.
A questo punto risulta evidente che il tutto si riduce ad escogitare un modo per ottenere in modo automatico gli array $u_1,u_2,...,u_9,u_10$.
Ed è qui che entra in gioco la funzione:
bool next_combination(unsigned int n, unsigned int k, unsigned int u[k]);
Essa:
- per $u={0,1,2}$ restituirà true e modificherà il suddetto array in $u={0,1,3}$;
- per $u={0,1,3}$ restituirà true e modificherà il suddetto array in $u={0,1,4}$;
...
- per $u={1,3,4}$ restituirà true e modificherà il suddetto array in $u={2,3,4}$;
- per $u={2,3,4}$ restituirà false.
Quindi per risolvere l'esercizio che ho proposto all'inizio di questo messaggio, non resta altro che implementare la funzione next_combination() utilizzando i suggerimenti che ti ho dato nel precedente post. Inizia a buttare giù qualche riga di codice, poi nel caso possiamo ragionarci insieme.
Scusami ma ho ancora qualche dubbio: come fà l'indice dell'array u[k] a essere una variabile? Prima di modificare l'array deve stampare quello precedente, giusto? Comunque ho provato a fare questo ma dubito sia giusto:
bool next_combination(int n, int k, int u[k])
{
for (int i = 0; i < k; i++)
{
int max = n - k + i;
if (u[k] < max)
{
u[k]= u[k]++;
}
else
{
u[k]= u[k]--;
}
}
for (int j = 0; j < k; j++)
cout << u[j] << endl;
return;
}
Ti posto direttamente il codice, in questo modo ti risulterà più chiaro il mio ragionamento:
Ora non resta che adattare il codice al tuo esercizio. Se qualcosa non ti è chiaro chiedi pure.
#include <iostream>
//stampare a schermo tutte le combinazioni semplici delle prime 5 lettere dell'alfabeto prese 3 alla volta.
using namespace std;
bool next_combination(unsigned int n, unsigned int k, unsigned int *u)
{
for(unsigned int i = 0; i < k; ++i)
{
if(u[k - i - 1] < n - i - 1) //il secondo termine rappresenta il massimo relativo al generico elemento
{
++u[k - i - 1];
for(unsigned int j = k - i; j < k; ++j)
{
u[j] = u[j - 1] + 1;
}
return true;
}
}
return false;
}
int main()
{
const unsigned int n = 5;
const unsigned int k = 3;
char v[n] = {'a', 'b', 'c', 'd', 'e'};
unsigned int u[k] = {0, 1, 2};
do
{
for(unsigned int i = 0; i < k; ++i)
{
cout << v[u[i]] << " ";
}
cout << endl;
}
while(next_combination(n, k, u));
}Ora non resta che adattare il codice al tuo esercizio. Se qualcosa non ti è chiaro chiedi pure.
Ok, ma in pratica invece di utilizzare i numeri, tu hai creato un array di char. Ora per far variare k bisogna incapsulare tutto in un ciclo, in modo che stampi tutte le combinazioni con 1, 2..n-1 element, giusto? Il codice penso comunque di averlo capito.
Ok, ma in pratica invece di utilizzare i numeri, tu hai creato un array di char.
In realtà l'ho fatto per sottolineare che il nostro set di $n$ elementi contenuti nell'array $v$ può essere costituito da elementi di qualsiasi tipo (int, char, stringhe, struct, altri array, etc...) e ordinati in vario modo (in ordine crescente, decrescente o disordinati). L'idea è proprio quella di sganciarsi dall'arbitrarietà dell'array $v$ lavorando direttamente su un secondo array $u$ con le seguenti caratteristiche:
- tipo int;
- dimensione $k$;
- inizializzato con valori che vanno da $0$ a $k-1$ disposti in ordine crescente.
Tale array non contiene altro, come già detto in precedenza, che gli indici relativi alla generica combinazione. Ad ogni chiamata della funzione next_combination() l'array $u$ viene aggiornato con gli indici della combinazione successiva.
Ora per far variare k bisogna incapsulare tutto in un ciclo, in modo che stampi tutte le combinazioni con 1, 2..n-1 element, giusto?
Sì, ma $k$ deve variare tra $1$ e $n$ e non tra $1$ e $n-1$.
Va bene. Quindi, per completare il programma, bisogna inserire u[k] in un ciclo che fa variare il numero di elementi, ovvero gli indici. Quindi all'inizio sarà: {0}, {0,1}, {0,1,2}, {0,1,2,3}, {0,1,2,3,4}. Mi hai corretto, giustamente da 1 a n.
Salve.
Per ottenere la lista ordinata dei sottoinsiemi di $k$ elementi presi da un insieme di $n$ ho utilizzato un arcaico "Visual Basic" (del secolo scorso) che però funziona ancora alla perfezione; ho impostato un ciclo For - Next per incrementare il numero degli elementi dell'array da 1 ad n ed ho poi dovuto escogitare una routine personale per il cambio degli indici, non potendo usufruire della funzione next_combination di C++. Qualche riga di programma in più e il risultato è stato raccolto su una List specifica. Come già segnalato il numero dei sottoinsiemi risulta dalla sommatoria delle combinazioni di $1, 2, 3 ... n$ elementi quindi:
$ x=\sum_{k=1}^\n\frac{(n!)}{(n-k)!*(k!)} $ con l'esclusione dell'insieme vuoto.
equivalente a $2^n - 1$ sottoinsiemi
Per n = 14 la lista dei 16384 sottoinsiemi è apparsa dopo 7 secondi.
Per ottenere la lista ordinata dei sottoinsiemi di $k$ elementi presi da un insieme di $n$ ho utilizzato un arcaico "Visual Basic" (del secolo scorso) che però funziona ancora alla perfezione; ho impostato un ciclo For - Next per incrementare il numero degli elementi dell'array da 1 ad n ed ho poi dovuto escogitare una routine personale per il cambio degli indici, non potendo usufruire della funzione next_combination di C++. Qualche riga di programma in più e il risultato è stato raccolto su una List specifica. Come già segnalato il numero dei sottoinsiemi risulta dalla sommatoria delle combinazioni di $1, 2, 3 ... n$ elementi quindi:
$ x=\sum_{k=1}^\n\frac{(n!)}{(n-k)!*(k!)} $ con l'esclusione dell'insieme vuoto.
equivalente a $2^n - 1$ sottoinsiemi
Per n = 14 la lista dei 16384 sottoinsiemi è apparsa dopo 7 secondi.
Da quel che so non esiste una funzione next_combination() fornita dalla libreria standard del C++.
Ma i 7'' quali attività comprendono? In ogni caso il dato interessante sarebbe il tempo relativo alla sola generazione delle combinazioni.
Per le combinazioni non è molto difficile, se invece parliamo di permutazioni la faccenda si complica un po'!
Ma i 7'' quali attività comprendono? In ogni caso il dato interessante sarebbe il tempo relativo alla sola generazione delle combinazioni.
ho poi dovuto escogitare una routine personale per il cambio degli indici
Per le combinazioni non è molto difficile, se invece parliamo di permutazioni la faccenda si complica un po'!
Ho ripreso il problema che ho lasciato in sospeso dopo mesi, per mancanza di tempo non l'ho terminato. Volevo capire bene il perchè dell'algoritmo proposto da SuperSquirrel, in particolare come ha dedotto la formula che indica il valore massimo che ogni elemento della combinazione deve raggiungere: $MAX(i)=n-k+i$. C'è un modo intuititivo per arrivarci?
Quella formula si riferisce ad un insieme di $n$ elementi ben preciso, costituito da interi che vanno da $0$ a $n-1$. Mesi fa ti chiesi quali fossero le combinazioni semplici in base $3$ dell'insieme ${0, 1, 2, 3, 4}$ (in pratica $n=5$ e $k=3$) e tu scrivesti:
Ovviamente questo è solo uno dei tanti modi in cui le suddette combinazioni possono essere esplicitate, ma utilizzando questo approccio risulta evidente che l'ultima combinazione, che coincide con gli ultimi $k$ elementi dell'insieme di partenza, è costituita dai massimi valori che gli elementi in una determinata posizione (o caratterizzati da un determinato indice, se preferisci) possono raggiungere.
La formula che ti proposi all'epoca, e che tu hai riportato nel post precedente, è solo uno dei tanti modi di formalizzare il concetto appena esposto.
"ZfreS":
sono: {0,1,2} {0,1,3} {0,1,4} {0,2,3} {0,2,4} {0,3,4} {1,2,3} {1,2,4} {1,3,4} {2,3,4}.
Ovviamente questo è solo uno dei tanti modi in cui le suddette combinazioni possono essere esplicitate, ma utilizzando questo approccio risulta evidente che l'ultima combinazione, che coincide con gli ultimi $k$ elementi dell'insieme di partenza, è costituita dai massimi valori che gli elementi in una determinata posizione (o caratterizzati da un determinato indice, se preferisci) possono raggiungere.
La formula che ti proposi all'epoca, e che tu hai riportato nel post precedente, è solo uno dei tanti modi di formalizzare il concetto appena esposto.
"Super Squirrel":
Da quel che so non esiste una funzione next_combination() fornita dalla libreria standard del C++.
Ma i 7'' quali attività comprendono? In ogni caso il dato interessante sarebbe il tempo relativo alla sola generazione delle combinazioni.
Per curiosità ho provato una versione ricorsiva, di cui non sono neanche troppo sicuro, sul mio hardware modesto siamo ben sotto i 7 secondi d'esecuzione:
#include <stdio.h>
#include <stdlib.h>
#define N 15
static void print_comb(const int *v, const int k)
{
int i;
printf("[%2d", v[0]);
for (i = 1; i < k; ++i) {
printf(", %2d", v[i]);
}
puts("]");
}
static void gen_comb(int *v, const int p, const int k)
{
int i;
if (p < k) {
if (0 == p) {
for (i = 1; i < N; ++i) {
v[p] = i;
gen_comb(v, p + 1, k);
}
}
else {
for (i = v[p - 1] + 1; i < N; ++i) {
v[p] = i;
gen_comb(v, p + 1, k);
}
}
}
else {
print_comb(v, k);
}
}
int main(void)
{
int i;
int v[N];
for (i = 1; i < N; ++i) {
gen_comb(v, 0, i);
}
return EXIT_SUCCESS;
}
C'è da dire che il tempo d'esecuzione, come già anticipato, cresce in maniera disgustosa per cui ha poco senso buttare numeri come 20-30, perché tra i 2 estremi c'è tanta differenza.
Ok, osservando le combinazioni si nota che ogni elemento raggiunge un valore massimo, ma hai detto che i sono diversi modi di formalizzarlo, la mia domanda è: come ci si arriva? Quella formula è sempre valida?
"Obidream":
Per curiosità ho provato una versione ricorsiva, di cui non sono neanche troppo sicuro, sul mio hardware modesto siamo ben sotto i 7 secondi d'esecuzione...
Per l'array v credo sia sufficiente una dimensione pari a $k$, inoltre, affinché siano calcolate le combinazioni semplici di $n$ (e non $n-1$) elementi, bisogna modificare la condizione dei for all'interno della funzione gen_comb() in <=N.
Apportando le suddette modifiche e qualche piccola semplificazione ho ottenuto il seguente codice:
#include <stdio.h>
#define N 7
#define K 4
void print_comb(const unsigned int *v)
{
for(unsigned int i = 0; i < K; ++i)
{
printf("%2d ", v[i]);
}
printf("\n");
}
void gen_comb(unsigned int *v, const unsigned int p)
{
if(p < K)
{
unsigned int i = 1;
if(p)
{
i += v[p - 1];
}
for( ; i <= N; ++i)
{
v[p] = i;
gen_comb(v, p + 1);
}
}
else
{
print_comb(v);
}
}
int main()
{
unsigned int v[K];
gen_comb(v, 0);
return 0;
}Per $n=30$ e $k=19$, e rimuovendo l'output, il tempo di esecuzione si aggira sui 18''. Nelle stesse condizioni il programma che ho postato nelle pagine precedenti impiega circa 2''. Ora non so quanto sia rigoroso il test che ho effettuato, ma penso che il punto sia un altro, ossia che una versione ricorsiva sia di più difficile utilizzo rispetto ad una iterativa in grado di passare da una generica combinazione a quella successiva (per esempio nel tuo codice la funzione print_comb() deve essere richiamata per forza dalla funzione gen_comb() e non dal main()).
"ZfreS":
Ok, osservando le combinazioni si nota che ogni elemento raggiunge un valore massimo, ma hai detto che i sono diversi modi di formalizzarlo, la mia domanda è: come ci si arriva? Quella formula è sempre valida?
Come già detto nel precedente post, quella formula è sempre valida nel momento in cui il set di elementi è costituito dagli interi che vanno da $0$ a $n-1$ e le combinazioni sono esplicitate utilizzando l'approccio:
"ZfreS":
sono: {0,1,2} {0,1,3} {0,1,4} {0,2,3} {0,2,4} {0,3,4} {1,2,3} {1,2,4} {1,3,4} {2,3,4}.
Per quanto riguarda l'altra domanda credo di non aver ben capito quale sia il tuo dubbio!
Provo a metterla diversamente:
- il massimo valore assumibile dall'ultimo elemento della generica combinazione è $n-1$;
- il massimo valore assumibile dal penultimo elemento della generica combinazione è $n-2$;
- il massimo valore assumibile dal terzultimo elemento della generica combinazione è $n-3$;
- ...
Ovviamente tale formulazione è equivalente a quella postata in precedenza $MAX(i)=n-k+i$
Hai chiarito tutto, grazie mille superSquirrel!
Super Squiller, ritorno per l'ennesima volta sull'argomento, dopo un po di tempo riprendo sempre dei vecchi problemi per vedere se li avevo capiti bene la prima volta, e fino a u certo puto era vero, però l'ultima volta non avevo prestato attenzione a questo ciclo:
Sinceramente non ho ben capito cosa fa questo ciclo, ma ripeto l'altra volta er concentrato su un altro spetto del problema e non ci ho fatto troppa attenzione. Oggi, provando a riscrivere il codice arrivo al punto di non riuscire a continuare come se mi fossi dimenticato una parte del codice, ed in effetti è così.
Non è che gentilmente potresti spiegarmi cosa fa esattamente quel ciclo?
for(unsigned int j = k - i; j < k; ++j)
{
u[j] = u[j - 1] + 1;
}
return true;
Sinceramente non ho ben capito cosa fa questo ciclo, ma ripeto l'altra volta er concentrato su un altro spetto del problema e non ci ho fatto troppa attenzione. Oggi, provando a riscrivere il codice arrivo al punto di non riuscire a continuare come se mi fossi dimenticato una parte del codice, ed in effetti è così.
Non è che gentilmente potresti spiegarmi cosa fa esattamente quel ciclo?
Rieccoci qua! 
Praticamente partendo dall'elemento immediatamente successivo a quello modificato dall'istruzione
quindi dall'elemento di indice
$j=(k-i-1)+1=k-i$
e proseguendo fino alla fine dell'array u (definita dalla condizione $j
Riprendendo l'immagine

consideriamo per esempio la combinazione n°6:
- partendo dalla fine abbiamo che l'elemento di indice i=2 è uguale al massimo per quella posizione (ossia 4);
- passiamo quindi all'elemento di indice i=1, ma anche lui è uguale al relativo massimo (ossia 3);
- passiamo allora all'elemento di indice i=0, il quale, essendo minore del relativo massimo (che è 2), può essere incrementato passando da 0 al valore 1.
Ed è proprio qui che entra in gioco quel ciclo for, il quale, modificando gli elementi di indici i=1 e i=2, ci consente di avere come combinazione n°7 la sequenza
1 2 3
al posto della sequenza
1 3 4
Praticamente partendo dall'elemento immediatamente successivo a quello modificato dall'istruzione
++u[k - i - 1];
quindi dall'elemento di indice
$j=(k-i-1)+1=k-i$
e proseguendo fino alla fine dell'array u (definita dalla condizione $j
Riprendendo l'immagine

consideriamo per esempio la combinazione n°6:
- partendo dalla fine abbiamo che l'elemento di indice i=2 è uguale al massimo per quella posizione (ossia 4);
- passiamo quindi all'elemento di indice i=1, ma anche lui è uguale al relativo massimo (ossia 3);
- passiamo allora all'elemento di indice i=0, il quale, essendo minore del relativo massimo (che è 2), può essere incrementato passando da 0 al valore 1.
Ed è proprio qui che entra in gioco quel ciclo for, il quale, modificando gli elementi di indici i=1 e i=2, ci consente di avere come combinazione n°7 la sequenza
1 2 3
al posto della sequenza
1 3 4
Benissimo Squirrel, credo di aver capito. Se per esempio considero la combinazione n°4, in posizione i=2 devo ancra raggiungere il massimo per quella posizione, quindi al prossimo ciclo viene incrementato, mentre vengono lasciati fissi gli altri, cosicchè i=0 => j=3 che rende subito falsa j
Tutor AI
Ciao! Sono il tuo Tutor AI, il compagno ideale per uno studio interattivo. Utilizzo il metodo maieutico per affinare il tuo ragionamento e la comprensione. Insieme possiamo:
- Risolvere un problema di matematica
- Riassumere un testo
- Tradurre una frase
- E molto altro ancora...
Il Tutor AI di Skuola.net usa un modello AI di Chat GPT.
Per termini, condizioni e privacy, visita la relativa pagina.
Per termini, condizioni e privacy, visita la relativa pagina.






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo