Problema di combinatoria
Ho questo problemino: generare tutti i sottoinsiemi di un insieme dato, ordinato per dimensione.
Per esempio: {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}.
Il problema in questo caso non è tanto l'implementazione dell'algoritmo, ma capire come ottenere l'algoritmo. Devo implementare qualcosa relativo al calcolo combinatorio per risolverlo?
Potreste darmi una pista su cui ragionare?
Per esempio: {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}.
Il problema in questo caso non è tanto l'implementazione dell'algoritmo, ma capire come ottenere l'algoritmo. Devo implementare qualcosa relativo al calcolo combinatorio per risolverlo?
Potreste darmi una pista su cui ragionare?
Risposte
Un generico sottoinsieme di un insieme dato è un insieme in cui ciascun elemento c'è oppure non c'è. Il numero di sottoinsiemi è quindi dato da tutte le combinazioni possibili di elementi che ci sono o non ci sono. Per esempio, se l'insieme di partenza è {1,2,3}, puoi vedere il sottoinsieme {1,2} come il numero binario 110, eccetera.
Spero che l'indizio sia utile, ma non ne sono sicurissimo
Spero che l'indizio sia utile, ma non ne sono sicurissimo
La tua osservazione mi sembra corretta, ho avuto perciò un'idea basato su questo, ma penso che richieda una dimostrazione matematica. Supponiamo che l'insieme sia già ordinato: {1,2,3,4,5}. I sottoinsiemi sono:
{1,2} {2,3} {3,4} {4,5}
{1,3} {2,4} {3,5}
{1,4} {2,5}
{1,5}
In pratica ho notato questo ordine, poi ci sono da aggiungere tutti quelli con gli elementi singoli quindi: {1} {2} {3} {4} {5}
Aspetto la risposta di qualcuno esperto, ma intanto questa è una mia idea di partenza. Poi è da vedere il metodo che le ordina mentre crea i sottoinsiemi.
{1,2} {2,3} {3,4} {4,5}
{1,3} {2,4} {3,5}
{1,4} {2,5}
{1,5}
In pratica ho notato questo ordine, poi ci sono da aggiungere tutti quelli con gli elementi singoli quindi: {1} {2} {3} {4} {5}
Aspetto la risposta di qualcuno esperto, ma intanto questa è una mia idea di partenza. Poi è da vedere il metodo che le ordina mentre crea i sottoinsiemi.
Quelli non sono tutti i sottoinsiemi però.
Dal punto di vista dell'implementazione, un approccio ricorsivo potrebbe funzionare se l'insieme non è gigantesco.
Dal punto di vista dell'implementazione, un approccio ricorsivo potrebbe funzionare se l'insieme non è gigantesco.
Non considero {1,2} e {2,1} come sottoinsiemi diversi. L'algoritmo deve prestarsi bene anche per insiemi di 50 elementi. Quindi penso che l'approccio ricorsivo non sia la miglior soluzione.
"ZfreS":
Non considero {1,2} e {2,1} come sottoinsiemi diversi.
Nemmeno io. Mancano tutti i sottoinsiemi di tre elementi, così come quelli di quattro elementi.
"ZfreS":
L'algoritmo deve prestarsi bene anche per insiemi di 50 elementi. Quindi penso che l'approccio ricorsivo non sia la miglior soluzione.
Mmm, 50 sono tanti in effetti :S
Ho risolto l'esercizio al volo e lo sto eseguendo in Python. Non è una passeggiata con 50 elementi.
Se li vuoi conservare tutti in memoria avrai anche problemi di spazio. Qual è esattamente il tuo obiettivo?
Hai ragione, mancano tutti gli altri, quindi deve essere semplice. Tu hai già implementato? Beh, non li devo conservare in memoria, dato che il fine dell'esercizio non è tanto la gestione delle risorse quanto l'algoritmo che crea e ordina i sottoinsiemi.
Ok, ma generarli in ordine qualsiasi e poi ordinarli è più semplice che generarli direttamente in ordine. Se non li puoi memorizzare tutti insieme significa che li devi generare già nell'ordine giusto.
Ok, mettiamola in questo modo: i numeri disordinati verranno memorizzati in un array nel main, non a runtime; poi man mano che vengono ordinati vengono anche memorizzati (non se ne può fare a meno). L'importante ora è capire come funziona l'algoritmo.
Se ho ben capito, nel caso in cui gli elementi fossero $n=5$, il risultato dovrebbe essere il seguente?
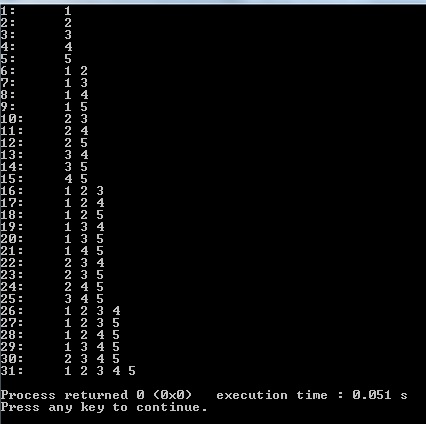
Secondo me la cosa più semplice è implementare una funzione in grado di generare tutte le combinazioni semplici di $n$ elementi presi $k$ alla volta e poi mettere tale funzione all'interno di un ciclo che fa variare $k$ da 1 a $n$.

Secondo me la cosa più semplice è implementare una funzione in grado di generare tutte le combinazioni semplici di $n$ elementi presi $k$ alla volta e poi mettere tale funzione all'interno di un ciclo che fa variare $k$ da 1 a $n$.
Solo come piccola osservazione.. Il numero di sottoinsiemi di un insieme dato è \(2^n\). Per \(n = 50\) hai quindi \(2^{50} = 1125899906842624 \approx 10^{15}\) (se ho contato bene le cifre..). Anche supponendo di metterci un nanosecondo a trovarne uno, ci metteresti \(10^6\) secondi (quasi 12 giorni). E questo solo per iterare su ognuno di essi. Se li devi memorizzare, supponendo di usare solo 50 bit, sono qualcosa tipo 5000 TB credo..
Si SuperSquirrel, l'output aspettato è proprio quello. Provo arealizzare ciò che dici.
In effetti 50 sono troppi, diciamo allora 20-30.
In effetti 50 sono troppi, diciamo allora 20-30.
Ma per generare tutte le combinazioni, utilizzo la formula classica o c'è qualche altro modo?
Il metodo più semplice è ovviamente quello di usare una funzione ricorsiva. Qual'è la formula classica a cui stai facendo riferimento?
Ho provato con 30 elementi e impiega circa 29'', ovviamente rimuovendo l'output.
La mia implementazione non è ricorsiva e si basa sulla modifica di un array di $k$ elementi contenente gli indici della generica combinazione semplice. I suddetti indici si riferiscono ad un secondo array che contiene gli $n$ elementi che costituiscono l'insieme di partenza.
La mia implementazione non è ricorsiva e si basa sulla modifica di un array di $k$ elementi contenente gli indici della generica combinazione semplice. I suddetti indici si riferiscono ad un secondo array che contiene gli $n$ elementi che costituiscono l'insieme di partenza.
Più per curiosità che per altro, quanto ci impiega la versione ricorsiva? Stai usando Python?
La formula classica a cui mi riferisco è il coefficiente binomiale $(n!)/(k!(n-k)!)$. Questa è la formula delle combinazioni semplici, penso quella che ha implementato Super Squirrel.
Ma vuoi ottenere solo il numero di questi sottoinsiemi o la loro lista? Perché se è solo il numero l'esercizio è molto più semplice.
"apatriarca":
Più per curiosità che per altro, quanto ci impiega la versione ricorsiva? Stai usando Python?
Non saprei, in quanto la funzione che genera la combinazione successiva è iterativa. Utilizzo C/C++.
In pratica l'implementazione può essere schematizzata nel seguente modo:
bool next_combination(unsigned int n, unsigned int k, unsigned int u[k])
{
...
}
int main()
{
const unsigned int n = 5;
const unsigned int k = 3; //per esempio
char v[n] = {a, b, c, d, e};
unsigned int u[k] = {0, 1, 2}
do
{
for(unsigned int i = 0; i < k; ++i)
{
cout << v[u[i]] << " ";
}
cout << endl;
}
while(next_combination(n, k, u));
}La formula classica a cui mi riferisco è il coefficiente binomiale n!k!(n−k)!. Questa è la formula delle combinazioni semplici, penso quella che ha implementato Super Squirrel.
Come detto da apatriarca, quella formula è utile per trovare il numero di combinazioni, non per ottenerne la lista!
No, la lista mi serve, ma pensavo che comunque per ottenere le combinazioni servisse la formula. Ma la funzione bool rimane vuota?
Qualcosa ci va pur messo! 
Scherzi a parte, non è difficile, puoi arrivarci da solo. Indizio: quali sono le combinazioni semplici in base 3 dell'insieme
{0, 1, 2, 3, 4}
?
Scherzi a parte, non è difficile, puoi arrivarci da solo. Indizio: quali sono le combinazioni semplici in base 3 dell'insieme
{0, 1, 2, 3, 4}
?




 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo