[C] Compilatore e divisione
Ciao, personalmente non conosco il linguaggio assembly, ma per caso da una discussione è emerso che il compilatore per effettuare la divisione intera $D/18$ effettuasse il prodotto tra $D$ e il numero $954437177$, per poi eseguire uno shift a destra di $34$ posizioni.
Dal momento che la cosa mi incuriosiva, ho deciso di rifletterci un po' su, e la prima cosa che mi è venuta in mente per "trasformare" una divisione in una moltiplicazione è quella di moltiplicare il dividendo per l'inverso del divisore:
$D/18=1/2(D/9)=1/2(D*1/9)$
Essendo $9=(1001)_2$ ho svolto la divisione $1/9$ in binario
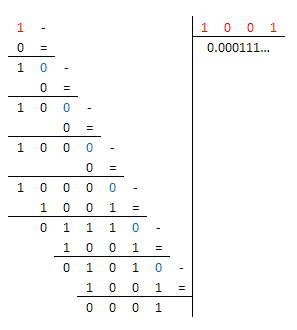
Dal momento che $1/9$ non può essere rappresentato in binario in modo esatto, ho pensato di approssimare la parte dopo la virgola in 32 bit (in modo che, ipotizzando che anche $D$ sia un intero a 32 bit, il loro prodotto possa essere espresso attraverso una variabile intera a 64 bit):
$1/9=1/(1001)_2=(0.bar(000111))_2\approx(0.000|11100011100011100011100011100011|)_2=$
$=(11100011100011100011100011100011)_2/2^(32+3)$
In definitiva quindi ottengo che la parte intera della suddetta divisione può essere calcolata come:
$[D/18]=[1/2(D*(0.bar(000111))_2)]=D*(11100011100011100011100011100011)_2$ \(\gg(32+3+1)\)
E' evidente che i $(11100011100011100011100011100011)_2=(3817748707)_(10)$ e $36$ ottenuti siano diversi dai $954437177$ e $34$ utilizzati dal compilatore, anche se utilizzando per l'approssimazione 30 bit e non 32 i numeri tornano "quasi" del tutto:
$D*((11100011100011100011100011100011)_2$ \(\gg2)\gg34=\)
\(=D*954437176\gg34\)
"Quasi" nel senso che il secondo fattore è più piccolo di un'unità rispetto a quello utilizzato dal compilatore.
-----------------------------------------------------------------------------------------------------------------------
In generale avremo quindi che
$[D/d]=D*q$ \(\gg\) $n$
con $q$ e $n$ che sono funzione di $d$.
Ovviamente affinché questo metodo sia performante i valori di $q$ e $n$ devono essere già noti; nel mio caso ho posto [inline]d_max = 100000[/inline] e ho utilizzato gli array [inline]v_q[/inline] e [inline]v_n[/inline] per contenere rispettivamente i valori di $q$ e $n$ calcolati (dalla funzione [inline]fun()[/inline] ) per valori di $d$ appartenenti all'intervallo $[1;100000]$. Quindi per esempio per accedere ai valori di $q$ e $n$ per $d = 41$ basterà accedere rispettivamente agli elementi [inline]v_q[41][/inline] e [inline]v_n[41][/inline].
Per testare il tutto ho disabilitato le ottimizzazioni del compilatore (affinché non venissero ignorati i cicli) e ho misurato i tempi necessari a calcolare [inline]N[/inline] volte una stessa divisione in diversi scenari:
- NATIVA: si riferisce alla divisione nativa del compilatore;
- OTTIMIZZATA CON ARRAY: si riferisce alla versione da me implementata con i valori di $q$ e $n$ prelevati rispettivamente dagli array [inline]v_q[/inline] e [inline]v_n[/inline]. Inoltre non ho utilizzato la funzione [inline]optimized_division()[/inline] per velocizzare il tutto evitando le varie chiamate a funzione (visto che la parola chiave [inline]inline[/inline] non sembra fare effetto);
- OTTIMIZZATA SENZA ARRAY: come sopra, ma i valori di $q$ e $n$ sono stati estratti dai due array per risparmiare sui tempi di accesso agli array.
Un altro test sulla velocità l'ho fatto misurando i tempi necessari a calcolare [inline]N[/inline] divisioni in cui il divisore è dato da [inline]rand() + 1[/inline] (che nel mio caso va bene essendo [inline]RAND_MAX < d_max[/inline] ).
Infine ho eseguito un test simile al precedente, ma questo volta non per calcolare i tempi, ma per valutare se la divisione nativa e la divisione da me implementata restituissero sempre gli stessi risultati.
Di seguito riporto il codice e l'output che ottengo lanciandolo:
A questo punto le questioni sono fondamentalmente due:
- ritenete che il compilatore utilizzi per la divisione intera un approccio simile a quello da me implementato?
Dai primi due test si evince relativamente ai tempi che [inline]OTTIMIZZATA CON ARRAY > NATIVA > OTTIMIZZATA SENZA ARRAY[/inline], il che mi fa pensare che il compilatore prelevi comunque i coefficienti da qualche parte, ma che questo prelievo sia più veloce rispetto a quello fatto dagli array globali [inline]v_q[/inline] e [inline]v_n[/inline]. Concordate sul fatto che anche il compilatore deve avere già a disposizione da qualche parte questi valori? E in tal caso dove e come ci accede?
- Dal terzo test si osserva che in alcuni casi (ossia per alcuni valori di $d$), la divisione da me implementata restituisce valori che sono più piccoli di un'unità rispetto al risultato reale. Come già ipotizzato in precedenza deve esserci qualche particolare che mi sfugge e di cui non ho tenuto conto nella fase di approssimazione; infatti se aumento i valori di $q$ di un'unità, i test fatti mi restituiscono sempre il risultato corretto. Come mai?
Dal momento che la cosa mi incuriosiva, ho deciso di rifletterci un po' su, e la prima cosa che mi è venuta in mente per "trasformare" una divisione in una moltiplicazione è quella di moltiplicare il dividendo per l'inverso del divisore:
$D/18=1/2(D/9)=1/2(D*1/9)$
Essendo $9=(1001)_2$ ho svolto la divisione $1/9$ in binario

Dal momento che $1/9$ non può essere rappresentato in binario in modo esatto, ho pensato di approssimare la parte dopo la virgola in 32 bit (in modo che, ipotizzando che anche $D$ sia un intero a 32 bit, il loro prodotto possa essere espresso attraverso una variabile intera a 64 bit):
$1/9=1/(1001)_2=(0.bar(000111))_2\approx(0.000|11100011100011100011100011100011|)_2=$
$=(11100011100011100011100011100011)_2/2^(32+3)$
In definitiva quindi ottengo che la parte intera della suddetta divisione può essere calcolata come:
$[D/18]=[1/2(D*(0.bar(000111))_2)]=D*(11100011100011100011100011100011)_2$ \(\gg(32+3+1)\)
E' evidente che i $(11100011100011100011100011100011)_2=(3817748707)_(10)$ e $36$ ottenuti siano diversi dai $954437177$ e $34$ utilizzati dal compilatore, anche se utilizzando per l'approssimazione 30 bit e non 32 i numeri tornano "quasi" del tutto:
$D*((11100011100011100011100011100011)_2$ \(\gg2)\gg34=\)
\(=D*954437176\gg34\)
"Quasi" nel senso che il secondo fattore è più piccolo di un'unità rispetto a quello utilizzato dal compilatore.
-----------------------------------------------------------------------------------------------------------------------
In generale avremo quindi che
$[D/d]=D*q$ \(\gg\) $n$
con $q$ e $n$ che sono funzione di $d$.
Ovviamente affinché questo metodo sia performante i valori di $q$ e $n$ devono essere già noti; nel mio caso ho posto [inline]d_max = 100000[/inline] e ho utilizzato gli array [inline]v_q[/inline] e [inline]v_n[/inline] per contenere rispettivamente i valori di $q$ e $n$ calcolati (dalla funzione [inline]fun()[/inline] ) per valori di $d$ appartenenti all'intervallo $[1;100000]$. Quindi per esempio per accedere ai valori di $q$ e $n$ per $d = 41$ basterà accedere rispettivamente agli elementi [inline]v_q[41][/inline] e [inline]v_n[41][/inline].
Per testare il tutto ho disabilitato le ottimizzazioni del compilatore (affinché non venissero ignorati i cicli) e ho misurato i tempi necessari a calcolare [inline]N[/inline] volte una stessa divisione in diversi scenari:
- NATIVA: si riferisce alla divisione nativa del compilatore;
- OTTIMIZZATA CON ARRAY: si riferisce alla versione da me implementata con i valori di $q$ e $n$ prelevati rispettivamente dagli array [inline]v_q[/inline] e [inline]v_n[/inline]. Inoltre non ho utilizzato la funzione [inline]optimized_division()[/inline] per velocizzare il tutto evitando le varie chiamate a funzione (visto che la parola chiave [inline]inline[/inline] non sembra fare effetto);
- OTTIMIZZATA SENZA ARRAY: come sopra, ma i valori di $q$ e $n$ sono stati estratti dai due array per risparmiare sui tempi di accesso agli array.
Un altro test sulla velocità l'ho fatto misurando i tempi necessari a calcolare [inline]N[/inline] divisioni in cui il divisore è dato da [inline]rand() + 1[/inline] (che nel mio caso va bene essendo [inline]RAND_MAX < d_max[/inline] ).
Infine ho eseguito un test simile al precedente, ma questo volta non per calcolare i tempi, ma per valutare se la divisione nativa e la divisione da me implementata restituissero sempre gli stessi risultati.
Di seguito riporto il codice e l'output che ottengo lanciandolo:
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <time.h>
#define MAX_d 100000
uint32_t v_q[MAX_d + 1];
uint32_t v_n[MAX_d + 1];
void fun(const uint32_t max_d)
{
for(uint32_t d = 2; d <= max_d; ++d)
{
uint32_t D = 1;
uint32_t d_2 = d;
uint32_t q = 0;
uint8_t n = 0;
for(; !(D & d_2); ++n, d_2 >>= 1);
if(d == d_2)
{
for(; D < d_2; ++n, D <<= 1);
for(uint8_t i = 0; i < 32; ++i)
{
q <<= 1;
if(D > d_2)
{
q |= 1;
D -= d_2;
}
D <<= 1;
}
v_q[d] = q;
v_n[d] = n;
}
else
{
v_q[d] = v_q[d_2];
v_n[d] = v_n[d_2] + n;
}
}
}
uint32_t optimized_division(const uint32_t D, const uint32_t d)
{
if(d < D)
{
return v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d];
}
return d == D ? 1 : 0;
}
int main()
{
uint32_t D = 941787252;
uint32_t d = 36248; // <= MAX_d
fun(MAX_d);
printf("OK\n\n");
uint32_t N = 50000000;
srand(time(0));
clock_t begin;
clock_t end;
begin = clock();
for(uint32_t i = 0; i < N; ++i)
{
D / d;
}
end = clock();
printf("%ux [ %u / %u = %u ] IN %fs (NATIVA)\n", N, D, d, D / d, (double)(end - begin) / CLOCKS_PER_SEC);
begin = clock();
for(uint32_t q = v_q[d], n = v_n[d], i = 0; i < N; ++i)
{
d < D ? (q ? (uint64_t)D * q >> 31 + n : D >> n) : (d == D ? 1 : 0);
}
end = clock();
printf("%ux [ %u / %u = %u ] IN %fs (OTTIMIZZATA SENZA ARRAY)\n", N, D, d, d < D ? (v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d]) : (d == D ? 1 : 0), (double)(end - begin) / CLOCKS_PER_SEC);
begin = clock();
for(uint32_t i = 0; i < N; ++i)
{
d < D ? (v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d]) : (d == D ? 1 : 0);
}
end = clock();
printf("%ux [ %u / %u = %u ] IN %fs (OTTIMIZZATA CON ARRAY)\n", N, D, d, d < D ? (v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d]) : (d == D ? 1 : 0), (double)(end - begin) / CLOCKS_PER_SEC);
begin = clock();
for(uint32_t i = 0; i < N; ++i)
{
D / (rand() + 1);
}
end = clock();
printf("\n%ux [ %u / (rand() + 1) ] IN %fs (NATIVA)\n", N, D, (double)(end - begin) / CLOCKS_PER_SEC);
begin = clock();
for(uint32_t i = 0; i < N; ++i)
{
d = rand() + 1;
d < D ? (v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d]) : (d == D ? 1 : 0);
}
end = clock();
printf("%ux [ %u / (rand() + 1) ] IN %fs (OTTIMIZZATA CON ARRAY)\n", N, D, (double)(end - begin) / CLOCKS_PER_SEC);
printf("\n------");
for(uint32_t cont = 0, i = 0; i < N && cont < 5; ++i)
{
d = rand() + 1;
if(D / d != optimized_division(D, d))
{
++cont;
printf("\n%u / %u = %u (NATIVA)", D, d, D / d);
printf("\n%u / %u = %u (OTTIMIZZATA)\n", D, d, optimized_division(D, d));
}
}
printf("------\n");
}OK 50000000x [ 941787252 / 36248 = 25981 ] IN 0.123000s (NATIVA) 50000000x [ 941787252 / 36248 = 25981 ] IN 0.119000s (OTTIMIZZATA SENZA ARRAY) 50000000x [ 941787252 / 36248 = 25981 ] IN 0.137000s (OTTIMIZZATA CON ARRAY) 50000000x [ 941787252 / (rand() + 1) ] IN 0.732000s (NATIVA) 50000000x [ 941787252 / (rand() + 1) ] IN 0.766000s (OTTIMIZZATA CON ARRAY) ------ 941787252 / 84 = 11211753 (NATIVA) 941787252 / 84 = 11211752 (OTTIMIZZATA) 941787252 / 294 = 3203358 (NATIVA) 941787252 / 294 = 3203357 (OTTIMIZZATA) 941787252 / 252 = 3737251 (NATIVA) 941787252 / 252 = 3737250 (OTTIMIZZATA) 941787252 / 14 = 67270518 (NATIVA) 941787252 / 14 = 67270517 (OTTIMIZZATA) 941787252 / 3 = 313929084 (NATIVA) 941787252 / 3 = 313929083 (OTTIMIZZATA) ------ Process returned 0 (0x0) execution time : 1.911 s Press any key to continue.
A questo punto le questioni sono fondamentalmente due:
- ritenete che il compilatore utilizzi per la divisione intera un approccio simile a quello da me implementato?
Dai primi due test si evince relativamente ai tempi che [inline]OTTIMIZZATA CON ARRAY > NATIVA > OTTIMIZZATA SENZA ARRAY[/inline], il che mi fa pensare che il compilatore prelevi comunque i coefficienti da qualche parte, ma che questo prelievo sia più veloce rispetto a quello fatto dagli array globali [inline]v_q[/inline] e [inline]v_n[/inline]. Concordate sul fatto che anche il compilatore deve avere già a disposizione da qualche parte questi valori? E in tal caso dove e come ci accede?
- Dal terzo test si osserva che in alcuni casi (ossia per alcuni valori di $d$), la divisione da me implementata restituisce valori che sono più piccoli di un'unità rispetto al risultato reale. Come già ipotizzato in precedenza deve esserci qualche particolare che mi sfugge e di cui non ho tenuto conto nella fase di approssimazione; infatti se aumento i valori di $q$ di un'unità, i test fatti mi restituiscono sempre il risultato corretto. Come mai?
Risposte
La divisione è in generale una operazione più lenta rispetto al prodotto. Per esempio, guardando nella tabella fornita da Agner Fog, troviamo che DIV ha una latenza di 10-12 cicli. La moltiplicazione su 32 o 64 bit (MUL) ha invece una latenza di soli 3 cicli e lo shift destro (SHR) ha una latenza di 1 ciclo. Quindi, nel caso in cui sia possibile calcolare direttamente l'inverso durante la compilazione, è conveniente fare uso di questo trucco. Nota che se avessi avuto una potenza di \(2\) si poteva convertire tutto in uno shift che era ancora più veloce.
Grazie per la risposta, ma quello che chiedevo era qualcosa di un po' più specifico:
Infatti faccio:
"utente__medio":
A questo punto le questioni sono fondamentalmente due:
- ritenete che il compilatore utilizzi per la divisione intera un approccio simile a quello da me implementato?
Dai primi due test si evince relativamente ai tempi che OTTIMIZZATA CON ARRAY > NATIVA > OTTIMIZZATA SENZA ARRAY, il che mi fa pensare che il compilatore prelevi comunque i coefficienti da qualche parte, ma che questo prelievo sia più veloce rispetto a quello fatto dagli array globali v_q e v_n. Concordate sul fatto che anche il compilatore deve avere già a disposizione da qualche parte questi valori? E in tal caso dove e come ci accede?
- Dal terzo test si osserva che in alcuni casi (ossia per alcuni valori di d), la divisione da me implementata restituisce valori che sono più piccoli di un'unità rispetto al risultato reale. Come già ipotizzato in precedenza deve esserci qualche particolare che mi sfugge e di cui non ho tenuto conto nella fase di approssimazione; infatti se aumento i valori di q di un'unità, i test fatti mi restituiscono sempre il risultato corretto. Come mai?
"apatriarca":
Nota che se avessi avuto una potenza di 2 si poteva convertire tutto in uno shift che era ancora più veloce.
Infatti faccio:
return v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d];
Il prodotto finale corrisponde più o meno a moltiplicare il dividendo per una approssimazione dell'inverso del divisore facendo uso di un certo numero di cifre/bit. Se scegliamo un divisore il cui inverso ha una rappresentazione binaria infinita, come è il caso di \(9\) nel nostro esempio, allora vediamo che troncando questo inverso otterremo sempre un risultato errato per dividendi che sono multipli del divisore. Infatti la nostra approssimazione sarà sempre inferiore dell'inverso, e quindi moltiplicando per il divisore otterremo un valore più piccolo di uno che verrà troncato a zero. Lo possiamo vedere per esempio in decimale:
\[
\begin{align*}
1/9 &= 0.\overline{1} \\
[1/9]_5 &= 0.11111 \\
9 \cdot [1/9]_5 = 9 \cdot 0.11111 &= 0.99999 < 1
\end{align*}
\]
Arrotondando possiamo ottenere anche valori maggiori dell'inverso che ci permettono di avere il risultato corretto in questo caso specifico. Tuttavia non è sempre così. Se prendiamo l'inverso binario di \(9\) uguale a \(0.\overline{000111}_2\) e ci fermiamo dopo \(6\) bit, avremo semplicemente \(0.000111_2\) che moltiplicato per \(1001_2\) non ci darà il risultato sperato. Darà infatti \(0.111111_2 < 1\).
A questo punto vale la pena di considerare l'arrotondamento verso infinito. Questo ci permette di arrivare sempre all'intero successivo per multipli del divisore. A questo punto ci rimane solo da scegliere una approssimazione abbastanza vicina per cui, se \(d\) è il nostro divisore e \(\delta\) la nostra approssimazione, allora
\[ \forall k. \; \lfloor (k\,d-1)\,\delta \rfloor = k-1. \]
Sappiamo che \(k\,d\,\delta = k + k\,\epsilon\) dove l'errore \(\epsilon < 2^{1-n}\)*. \(k\) è un intero e quindi lo possiamo estrarre ed eliminare con il corrispondente valore dall'altro lato ottenendo \(\lfloor k\epsilon - \delta \rfloor = -1\). Dobbiamo quindi mostrare che \(0 > k\,\epsilon - \delta > -1 \implies k\,\epsilon < \delta\) per ogni \(k\). Ogni dividendo che prendiamo in considerazione sarà minore di \(2^{32}\) per cui scegliamo \(n\) tale che
\[ k\,\epsilon < 2^{32+1-n}/d < 1/d < \delta \implies 33 < n. \]
Abbiamo quindi ottenuto il valore e il numero di bit usato dal compilatore.
* Qui avevo inizialmente scritto \(2^n\), ma in base ai miei esperimenti sembra che l'errore sia quello che ho scritto in seguito. Fa anche tornare i conti. La differenza credo sia dovuta al fatto che ci sono due fonti di errore: l'approssimazione di \(2^n/d\) (con errore minore di \(1\) e poi lo shift \(\gg n\).
\[
\begin{align*}
1/9 &= 0.\overline{1} \\
[1/9]_5 &= 0.11111 \\
9 \cdot [1/9]_5 = 9 \cdot 0.11111 &= 0.99999 < 1
\end{align*}
\]
Arrotondando possiamo ottenere anche valori maggiori dell'inverso che ci permettono di avere il risultato corretto in questo caso specifico. Tuttavia non è sempre così. Se prendiamo l'inverso binario di \(9\) uguale a \(0.\overline{000111}_2\) e ci fermiamo dopo \(6\) bit, avremo semplicemente \(0.000111_2\) che moltiplicato per \(1001_2\) non ci darà il risultato sperato. Darà infatti \(0.111111_2 < 1\).
A questo punto vale la pena di considerare l'arrotondamento verso infinito. Questo ci permette di arrivare sempre all'intero successivo per multipli del divisore. A questo punto ci rimane solo da scegliere una approssimazione abbastanza vicina per cui, se \(d\) è il nostro divisore e \(\delta\) la nostra approssimazione, allora
\[ \forall k. \; \lfloor (k\,d-1)\,\delta \rfloor = k-1. \]
Sappiamo che \(k\,d\,\delta = k + k\,\epsilon\) dove l'errore \(\epsilon < 2^{1-n}\)*. \(k\) è un intero e quindi lo possiamo estrarre ed eliminare con il corrispondente valore dall'altro lato ottenendo \(\lfloor k\epsilon - \delta \rfloor = -1\). Dobbiamo quindi mostrare che \(0 > k\,\epsilon - \delta > -1 \implies k\,\epsilon < \delta\) per ogni \(k\). Ogni dividendo che prendiamo in considerazione sarà minore di \(2^{32}\) per cui scegliamo \(n\) tale che
\[ k\,\epsilon < 2^{32+1-n}/d < 1/d < \delta \implies 33 < n. \]
Abbiamo quindi ottenuto il valore e il numero di bit usato dal compilatore.
* Qui avevo inizialmente scritto \(2^n\), ma in base ai miei esperimenti sembra che l'errore sia quello che ho scritto in seguito. Fa anche tornare i conti. La differenza credo sia dovuta al fatto che ci sono due fonti di errore: l'approssimazione di \(2^n/d\) (con errore minore di \(1\) e poi lo shift \(\gg n\).
"apatriarca":
A questo punto ci rimane solo da scegliere una approssimazione abbastanza vicina per cui, se \( d \) è il nostro divisore e \( \delta \) la nostra approssimazione, allora
\[ \forall k. \; \lfloor (k\,d-1)\,\delta \rfloor = k-1. \]
Sappiamo che \( k\,d\,\delta = k + k\,\epsilon \) dove l'errore \( \epsilon < 2^{1-n} \)*. \( k \) è un intero e quindi lo possiamo estrarre ed eliminare con il corrispondente valore dall'altro lato ottenendo \( \lfloor k\epsilon - \delta \rfloor = -1 \). Dobbiamo quindi mostrare che \( 0 > k\,\epsilon - \delta > -1 \implies k\,\epsilon < \delta \) per ogni \( k \). Ogni dividendo che prendiamo in considerazione sarà minore di \( 2^{32} \) per cui scegliamo \( n \) tale che
\[ k\,\epsilon < 2^{32+1-n}/d < 1/d < \delta \implies 33 < n. \]
Abbiamo quindi ottenuto il valore e il numero di bit usato dal compilatore.
* Qui avevo inizialmente scritto \( 2^n \), ma in base ai miei esperimenti sembra che l'errore sia quello che ho scritto in seguito. Fa anche tornare i conti. La differenza credo sia dovuta al fatto che ci sono due fonti di errore: l'approssimazione di \( 2^n/d \) (con errore minore di \( 1 \) e poi lo shift \( \gg n \).
Ho provato a seguire il tuo ragionamento, ma qui mi sono perso.
Per esempio partendo dall'inizio: cosa rappresentano $k$ e $delta$ ?
P.S.1
Mi sembra di capire che "l'arrotondamento verso infinito" corrisponde più o meno alla funzione [inline]ceil()[/inline], ossia se la parte decimale è nulla restituisce la parte intera e in caso contrario restituisce la parte intera incrementata di 1. Giusto?
P.S.2
Ho avuto modo di leggere anche il precedente post che hai rimosso, ma non ho risposto subito perché volevo riflettere meglio sulle considerazioni finali che facevi.
L'idea è che sostituisci \(D/d\) con \(D \cdot q \gg 2^n\). Posso interpretare \(q\) come un numero razionale \(\delta\) rappresentato in fixed-point (credo sia virgola fissa in italiano) con \(n\) bit di parte frazionaria. A questo punto lo shift è una conversione tra virgola fissa con \(n\) bit di parte frazionaria e un normale numero intero e possiamo anche vederla come la funzione [tt]floor[/tt] se interpretiamo il risultato come un numero frazionario senza parte frazionaria. Quando scrivo \(D \, \delta\) sto lavorando in virgola fissa o numeri reali mentre quando scrivo \(D \cdot q\) lo interpreto come un numero intero. Rappresento inoltre la divisione intera con \(\div\) e quella reale con \(/\).
L'arrotondamento verso infinito è [tt]ceil[/tt] se il numero è positivo e [tt]floor[/tt] se il numero è negativo. In pratica approssima un numero reale scegliendo l'intero più grande in valore assoluto. Di fatto siccome stiamo lavorando solo con numeri naturali qui possiamo interpretarlo come [tt]ceil[/tt]. Quindi nel mio caso sto usando \(\delta = \lceil 1/d \rceil_n\) dove \(\lceil \cdot \rceil_n\) significa che sto considerando \(n\) bit di parte frazionaria.
La moltiplicazione per un numero intero costante è una funzione monotona crescente e lo shift destro mantiene questa proprietà producendo una funzione costante a tratti. La divisione intera per una costante produce una funzione costante a tratti in cui i salti avvengono in corrispondenza dei multipli del divisore (quindi numeri nella forma \(k \, d\)). Se vogliamo che le due funzioni corrispondano abbiamo bisogno che il salto avvenga in corrispondenza dei multipli e che quindi sia uguale a \(k\) per il multiplo \(k \, d\) e uguale a \(k-1\) per il valore precedente \(k \, d - 1\).
La scelta di usare [tt]ceil[/tt] ci permette di stabilire che \(\delta \ge 1/d\) e che quindi \((k \, d) \, \delta \ge (k \, d)/d = k. \) Chiamo \(\epsilon = \delta - 1/d\) che sappiamo essere positivo.
A questo punto spero sia chiaro il resto, anche se mi accorgo di aver commesso un errore. Cerco di calcolare \( (k \cdot d - 1) q \gg n = \lfloor (k \, d - 1) \, \delta \rfloor \) provando sia uguale a \(k - 1\). Ho che
\[
\begin{align*}
(k \, d - 1) \, \delta &= (k \, d) \, \delta - 1 \, \delta \\
&= (k \, d)/d + (k \, d) \epsilon - \delta \\
&= k + k\,d\,\epsilon - \delta
\end{align*}
\]
A questo punto abbiamo che \(k\) è un numero intero e quindi può essere estratto dal [tt]floor[/tt]. Non ci rimane che dimostrare che \(\lfloor k\,d\,\epsilon - \delta \rfloor = - 1\). Ovviamente abbiamo che \(0 < \delta < 1\) (stiamo ignorando il caso \(d = 1\)) e che \(\epsilon \ge 0\). L'importante è quindi che \(k\,d\epsilon < \delta\). A questo punto abbiamo che \(k\,d < 2^{32},\) \(\epsilon < 2^{-n}\) e \(1/q \le \delta\) possiamo farne il logaritmo ottenendo:
\[ \log_2(k\,d) + \log_2(\epsilon) < 32 - n < -\log_2(d) \le \log_2(\delta) \]
Quindi \(n > \log_2(d) + 32\).
Questo risultato ci darebbe \(n = 36\) nel nostro caso. Tuttavia c'è un problema a cui non avevo pensato. Abbiamo bisogno che \(D \cdot q\) stia in un intero a \(64\) bit. Possiamo ovviamente considerare il risultato a 128 bit del prodotto e poi ricostruire il risultato ma non credo che il compilatore lo faccia. Questo significa che è necessario ridurre i valori possibili di \(D\) a quelli che ci permettono di rimanere nell'intero a 64 bit. Quindi abbiamo che \(D = k\,d < 2^{64-n}\) e quindi abbiamo \(2n > \log_2(d) + 64\) che ci fornisce effettivamente \(34\) come il compilatore.
L'arrotondamento verso infinito è [tt]ceil[/tt] se il numero è positivo e [tt]floor[/tt] se il numero è negativo. In pratica approssima un numero reale scegliendo l'intero più grande in valore assoluto. Di fatto siccome stiamo lavorando solo con numeri naturali qui possiamo interpretarlo come [tt]ceil[/tt]. Quindi nel mio caso sto usando \(\delta = \lceil 1/d \rceil_n\) dove \(\lceil \cdot \rceil_n\) significa che sto considerando \(n\) bit di parte frazionaria.
La moltiplicazione per un numero intero costante è una funzione monotona crescente e lo shift destro mantiene questa proprietà producendo una funzione costante a tratti. La divisione intera per una costante produce una funzione costante a tratti in cui i salti avvengono in corrispondenza dei multipli del divisore (quindi numeri nella forma \(k \, d\)). Se vogliamo che le due funzioni corrispondano abbiamo bisogno che il salto avvenga in corrispondenza dei multipli e che quindi sia uguale a \(k\) per il multiplo \(k \, d\) e uguale a \(k-1\) per il valore precedente \(k \, d - 1\).
La scelta di usare [tt]ceil[/tt] ci permette di stabilire che \(\delta \ge 1/d\) e che quindi \((k \, d) \, \delta \ge (k \, d)/d = k. \) Chiamo \(\epsilon = \delta - 1/d\) che sappiamo essere positivo.
A questo punto spero sia chiaro il resto, anche se mi accorgo di aver commesso un errore. Cerco di calcolare \( (k \cdot d - 1) q \gg n = \lfloor (k \, d - 1) \, \delta \rfloor \) provando sia uguale a \(k - 1\). Ho che
\[
\begin{align*}
(k \, d - 1) \, \delta &= (k \, d) \, \delta - 1 \, \delta \\
&= (k \, d)/d + (k \, d) \epsilon - \delta \\
&= k + k\,d\,\epsilon - \delta
\end{align*}
\]
A questo punto abbiamo che \(k\) è un numero intero e quindi può essere estratto dal [tt]floor[/tt]. Non ci rimane che dimostrare che \(\lfloor k\,d\,\epsilon - \delta \rfloor = - 1\). Ovviamente abbiamo che \(0 < \delta < 1\) (stiamo ignorando il caso \(d = 1\)) e che \(\epsilon \ge 0\). L'importante è quindi che \(k\,d\epsilon < \delta\). A questo punto abbiamo che \(k\,d < 2^{32},\) \(\epsilon < 2^{-n}\) e \(1/q \le \delta\) possiamo farne il logaritmo ottenendo:
\[ \log_2(k\,d) + \log_2(\epsilon) < 32 - n < -\log_2(d) \le \log_2(\delta) \]
Quindi \(n > \log_2(d) + 32\).
Questo risultato ci darebbe \(n = 36\) nel nostro caso. Tuttavia c'è un problema a cui non avevo pensato. Abbiamo bisogno che \(D \cdot q\) stia in un intero a \(64\) bit. Possiamo ovviamente considerare il risultato a 128 bit del prodotto e poi ricostruire il risultato ma non credo che il compilatore lo faccia. Questo significa che è necessario ridurre i valori possibili di \(D\) a quelli che ci permettono di rimanere nell'intero a 64 bit. Quindi abbiamo che \(D = k\,d < 2^{64-n}\) e quindi abbiamo \(2n > \log_2(d) + 64\) che ci fornisce effettivamente \(34\) come il compilatore.
Innanzitutto volevo ringraziarti per la disponibilità.
Relativamente al tuo ultimo post, l'ho riletto più volte, e adesso il tuo ragionamento mi è decisamente più chiaro. Ma anche se i singoli passaggi mi sono piuttosto chiari, ancora non riesco a metabolizzare bene il tutto...
Da quello che ho capito, stai dicendo che affinché \( [D \delta] \) (con \( \delta = \lceil 1/d \rceil_n \)) sia uguale a \( [D/d] \) per ogni \( D \in [0;2^{32}) \), devono verificarsi le seguenti due uguaglianze:
\( \begin{cases} [kd \delta]=k \\ [(kd-1) \delta]=k-1 \end{cases} \)
Da cui si ricava la condizione che deve rispettare $n$, ossia \( n > \log_2(d) + 32 \). Giusto?
Mi chiedevo però se la seconda uguaglianza non dovrebbe essere invece generalizzata come \( [(kd-a) \delta]=k-1 \) con \( a \in [1;d-1] \)?
Infine se ho per esempio $d=7$ e fisso $n=11$ (e quindi \( \delta=0.00100100101 \) e $q=(100100101)_2=(293)_(10)$), come faccio a calcolarmi il massimo valore di $D$ per cui questo metodo risulta ancora funzionante?
Da un semplice programmino ottengo che è $D=684$, infatti \( 685*293 \gg 11=98\) che è diverso da \( [685/7]=97 \).
Relativamente al tuo ultimo post, l'ho riletto più volte, e adesso il tuo ragionamento mi è decisamente più chiaro. Ma anche se i singoli passaggi mi sono piuttosto chiari, ancora non riesco a metabolizzare bene il tutto...
Da quello che ho capito, stai dicendo che affinché \( [D \delta] \) (con \( \delta = \lceil 1/d \rceil_n \)) sia uguale a \( [D/d] \) per ogni \( D \in [0;2^{32}) \), devono verificarsi le seguenti due uguaglianze:
\( \begin{cases} [kd \delta]=k \\ [(kd-1) \delta]=k-1 \end{cases} \)
Da cui si ricava la condizione che deve rispettare $n$, ossia \( n > \log_2(d) + 32 \). Giusto?
Mi chiedevo però se la seconda uguaglianza non dovrebbe essere invece generalizzata come \( [(kd-a) \delta]=k-1 \) con \( a \in [1;d-1] \)?
Infine se ho per esempio $d=7$ e fisso $n=11$ (e quindi \( \delta=0.00100100101 \) e $q=(100100101)_2=(293)_(10)$), come faccio a calcolarmi il massimo valore di $D$ per cui questo metodo risulta ancora funzionante?
Da un semplice programmino ottengo che è $D=684$, infatti \( 685*293 \gg 11=98\) che è diverso da \( [685/7]=97 \).
1. È corretto.
2. Stiamo facendo il floor di una funzione monotona crescente, per cui cioè il valore cresce al crescere del valore di input. Avremo quindi dei pezzi in cui il valore è costante e dei salti a determinati punti. Chiedendo che il risultato sia \(k\) ai multipli di \(d\) e ancora lo stesso valore dopo \(d-1\) è sufficiente per dimostrare che è lo stesso valore per ogni input intermedio. La dimostrazione per \(a > 1\) segue comunque facilmente dal caso \(a = 1\).
3. Non credo sia facile calcolare direttamente il risultato in questo modo. Usando l'equazione sopra ottengo infatti che è assicurato che funzioni fino a \(292\) che è ovviamente molto più piccolo del tuo valore. La ragione è che ho fatto delle maggiorazioni per arrivare a quel valore e quindi è forse possibile arrivare a valori molto più vicini. Ottieni probabilmente un valore più vicino se usi \(log_2(\epsilon)\) nella formula direttamente invece di \(-n\).
2. Stiamo facendo il floor di una funzione monotona crescente, per cui cioè il valore cresce al crescere del valore di input. Avremo quindi dei pezzi in cui il valore è costante e dei salti a determinati punti. Chiedendo che il risultato sia \(k\) ai multipli di \(d\) e ancora lo stesso valore dopo \(d-1\) è sufficiente per dimostrare che è lo stesso valore per ogni input intermedio. La dimostrazione per \(a > 1\) segue comunque facilmente dal caso \(a = 1\).
3. Non credo sia facile calcolare direttamente il risultato in questo modo. Usando l'equazione sopra ottengo infatti che è assicurato che funzioni fino a \(292\) che è ovviamente molto più piccolo del tuo valore. La ragione è che ho fatto delle maggiorazioni per arrivare a quel valore e quindi è forse possibile arrivare a valori molto più vicini. Ottieni probabilmente un valore più vicino se usi \(log_2(\epsilon)\) nella formula direttamente invece di \(-n\).
Chiaro.
Come hai ricavato il valore $292$?
"apatriarca":
Usando l'equazione sopra ottengo infatti che è assicurato che funzioni fino a $292$ che è ovviamente molto più piccolo del tuo valore.
Come hai ricavato il valore $292$?
Dalla formula (\(M\) è il massimo che vogliamo calcolare):
\[
\begin{align*}
\log_2(M) + \log_2(\epsilon) < \log_2(M) - n &< -\log_2(d) \le \log_2(\delta) \\
\log_2(M) &< n - \log_2(d) \\
M < 2^{11 - \log_2(7)} &\approx 292.57142857142867
\end{align*}
\]
Ho scritto il seguente piccolo script in Julia:
che mi restituisce \(682.6666666666407\) per cui sembra che la formula \(\log_2(M) + \log_2(\epsilon) < \log_2(\delta)\) sia abbastanza accurata (la differenza di due unità potrebbe essere dovuto a qualche errore di calcolo immagino).
\[
\begin{align*}
\log_2(M) + \log_2(\epsilon) < \log_2(M) - n &< -\log_2(d) \le \log_2(\delta) \\
\log_2(M) &< n - \log_2(d) \\
M < 2^{11 - \log_2(7)} &\approx 292.57142857142867
\end{align*}
\]
Ho scritto il seguente piccolo script in Julia:
δ(d, n) = ceil(1/d, digits=n, base=2) ϵ(d, n) = δ(d, n) - 1/d log₂ϵ(d, n) = log2(ϵ(d, n)) log₂M(d, n) = - log₂ϵ(d, n) - log2(d) M(d, n) = exp2(log₂M(d, n)) M(7, 11)
che mi restituisce \(682.6666666666407\) per cui sembra che la formula \(\log_2(M) + \log_2(\epsilon) < \log_2(\delta)\) sia abbastanza accurata (la differenza di due unità potrebbe essere dovuto a qualche errore di calcolo immagino).
Ho comunque provato la formula più precisa invece della approssimazione e viene che supporta tutti i numeri fino a \(2^{32}\) con soli \(34\) bit invece di averne bisogno di \(36\) come nella formula approssimata.
"apatriarca":
Ho scritto il seguente piccolo script in Julia:
δ(d, n) = ceil(1/d, digits=n, base=2) ϵ(d, n) = δ(d, n) - 1/d log₂ϵ(d, n) = log2(ϵ(d, n)) log₂M(d, n) = - log₂ϵ(d, n) - log2(d) M(d, n) = exp2(log₂M(d, n)) M(7, 11)
che mi restituisce \(682.6666666666407\) per cui sembra che la formula \(\log_2(M) + \log_2(\epsilon) < \log_2(\delta)\) sia abbastanza accurata (la differenza di due unità potrebbe essere dovuto a qualche errore di calcolo immagino).
Ma se la condizione originale da rispettare è \( k\,d\epsilon < \delta \), penso si possa fare anche a meno dei logaritmi, infatti con semplici passaggi si ottiene che \( k< \delta/(d \delta -1) \), e quindi a rigore l'unica inferenza che possiamo fare (posto \( A = [ \delta/(d \delta -1)] \)) è che $ A*d <= D_{MAX} < (A+1)*d $ . O sbaglio?
Nel nostro caso facendo i conti viene $ 679 <= D_{MAX} < 686 $.
La formula \(k\,d\,\epsilon < \delta\) considera solo i multipli di \(d\) ed è la ragione per cui hai ottenuto solo l'intervallo di valori all'interno del quale trovi il massimo. Bella trovata comunque, non ci avevo pensato ed è effettivamente più semplice. Nota che il passaggio a \(d\,\epsilon = d\delta - 1\) non è necessario perché sia \(\epsilon\) che \(d\) sono delle costanti per cui è solo un modo diverso di ottenere lo stesso valore.
Si può a questo punto ricavare anche \(M = A\,d + a\) osservando che devi avere \(A\,d\,\epsilon + a\,\delta < 1,\) da cui puoi semplicemente ricavare
\[ A\,(d\,\delta - 1) + a\,\delta = (A\,d + a)\,\delta - A = M\delta - A < 1 \implies M < (1 + A)/\delta \]
Ho modificato il codice con questa nuova logica:
Restituisce 684.
Si può a questo punto ricavare anche \(M = A\,d + a\) osservando che devi avere \(A\,d\,\epsilon + a\,\delta < 1,\) da cui puoi semplicemente ricavare
\[ A\,(d\,\delta - 1) + a\,\delta = (A\,d + a)\,\delta - A = M\delta - A < 1 \implies M < (1 + A)/\delta \]
Ho modificato il codice con questa nuova logica:
function max_dividend(d, n)
δ = ceil(1/d, digits=n, base=2)
A = floor(δ/(d*δ - 1))
return floor(Int64, (1 + A)/δ)
end
Restituisce 684.
Ottimo, passare da un intervallo di ampiezza $d$ al valore esatto è un passo in avanti non da poco!
Però non capisco da dove viene la condizione \( A\,d\,\epsilon + a\,\delta < 1 \).
Però non capisco da dove viene la condizione \( A\,d\,\epsilon + a\,\delta < 1 \).
Viene da
\[ A = \lfloor(A\,d + a)\,\delta\rfloor = \lfloor A\,d\,\delta + a\,\delta\rfloor = \lfloor A\,d\,(1/d + \epsilon) + a\,\delta\rfloor = A + \lfloor A\,d\,\epsilon + a\,\delta\rfloor\]
A questo punto rimuovendo A da entrambi i lati ti rimane che quello che hai nel floor è positivo e deve essere minore di uno perché il suo floor sia zero.
\[ A = \lfloor(A\,d + a)\,\delta\rfloor = \lfloor A\,d\,\delta + a\,\delta\rfloor = \lfloor A\,d\,(1/d + \epsilon) + a\,\delta\rfloor = A + \lfloor A\,d\,\epsilon + a\,\delta\rfloor\]
A questo punto rimuovendo A da entrambi i lati ti rimane che quello che hai nel floor è positivo e deve essere minore di uno perché il suo floor sia zero.
Chiaro, grazie!
Stavo cercando di ricapitolare il tutto, ma mi è sorto un dubbio. Il nostro scopo è dimostrare che \(D \div d = \lfloor D \delta \rfloor \) per determinati valori di $D$. Nell'uguaglianza appena scritta ho utilizzato il floor, ma l'operazione di troncamento \( [\cdot] \) sarebbe stata in questo caso del tutto equivalente, dal momento che stiamo considerando valori positivi.
Il discorso cambia invece quando consideriamo la condizione
\( \lfloor kd \epsilon - \delta\rfloor = -1\Rightarrow \begin{cases} kd \epsilon - \delta < 0 \\ kd \epsilon - \delta \geq -1 \end{cases} \)
o la condizione
\( [ kd \epsilon - \delta] = -1\Rightarrow \begin{cases} kd \epsilon - \delta \leq -1 \\ kd \epsilon - \delta > -2 \end{cases} \)
Su quali basi dovremmo decidere a priori se utilizzare il floor o il troncamento?
Stavo cercando di ricapitolare il tutto, ma mi è sorto un dubbio. Il nostro scopo è dimostrare che \(D \div d = \lfloor D \delta \rfloor \) per determinati valori di $D$. Nell'uguaglianza appena scritta ho utilizzato il floor, ma l'operazione di troncamento \( [\cdot] \) sarebbe stata in questo caso del tutto equivalente, dal momento che stiamo considerando valori positivi.
Il discorso cambia invece quando consideriamo la condizione
\( \lfloor kd \epsilon - \delta\rfloor = -1\Rightarrow \begin{cases} kd \epsilon - \delta < 0 \\ kd \epsilon - \delta \geq -1 \end{cases} \)
o la condizione
\( [ kd \epsilon - \delta] = -1\Rightarrow \begin{cases} kd \epsilon - \delta \leq -1 \\ kd \epsilon - \delta > -2 \end{cases} \)
Su quali basi dovremmo decidere a priori se utilizzare il floor o il troncamento?
Con floor possiamo estrarre valori interi dal floor senza che il risultato cambi, ma questo non è possibile nel caso del troncamento se, come in questo caso, passiamo da valori positivi a negativi.
Ho provato a ricapitolare il tutto riformulando alcune cose:
In questo modo viene anche meno la questione di distinguere tra floor e troncamento, in quanto non avendo a che fare con numeri negativi le due funzioni risultano del tutto equivalenti.
Passiamo ora dalla parte più "matematica" a quella più "informatica":
Quello che ho scritto è corretto o ho commesso qualche errore?
In questo modo viene anche meno la questione di distinguere tra floor e troncamento, in quanto non avendo a che fare con numeri negativi le due funzioni risultano del tutto equivalenti.
Passiamo ora dalla parte più "matematica" a quella più "informatica":
Quello che ho scritto è corretto o ho commesso qualche errore?
Una delle due questioni che ponevo nel post iniziale può oramai ritenersi abbondantemente risolta (o almeno credo), passo quindi all'altra.
Relativamente alla divisione nativa, nei casi in cui il divisore è una costante, i coefficienti (che io chiamo $Q$ e $n$) per quel determinato valore di $d$ possono essere tranquillamente calcolati in fase di compilazione; se invece per esempio [inline]d = rand() + 1[/inline] il discorso cambia e diventa necessario calcolare i coefficienti per [inline]RAND_MAX + 1[/inline] valori (che io vado a salvare negli array [inline]v_Q[RAND_MAX + 1][/inline] e [inline]v_n[RAND_MAX + 1][/inline]). La domanda quindi sorge spontanea: come si comporta il compilatore in questo caso?
Nella mia ignoranza, dando un'occhiata ai tempi quasi sovrapponibili
mi verrebbe da pensare che anche il compilatore (ammesso che utilizzi lo stesso procedimento di eseguire la divisione mediante una moltiplicazione ed uno shift) prelevi i coefficienti da qualche parte, e che questo prelievo sia leggermente più veloce rispetto a quello che io faccio dagli array globali [inline]v_Q[/inline] e [inline]v_n[/inline].
Concordate sul fatto che anche il compilatore deve avere già a disposizione da qualche parte questi valori? E in tal caso dove?
Relativamente alla divisione nativa, nei casi in cui il divisore è una costante, i coefficienti (che io chiamo $Q$ e $n$) per quel determinato valore di $d$ possono essere tranquillamente calcolati in fase di compilazione; se invece per esempio [inline]d = rand() + 1[/inline] il discorso cambia e diventa necessario calcolare i coefficienti per [inline]RAND_MAX + 1[/inline] valori (che io vado a salvare negli array [inline]v_Q[RAND_MAX + 1][/inline] e [inline]v_n[RAND_MAX + 1][/inline]). La domanda quindi sorge spontanea: come si comporta il compilatore in questo caso?
Nella mia ignoranza, dando un'occhiata ai tempi quasi sovrapponibili
50000000x [ 941787252 / (rand() + 1) ] IN 0.732000s (NATIVA) 50000000x [ 941787252 / (rand() + 1) ] IN 0.766000s (PERSONALE)
mi verrebbe da pensare che anche il compilatore (ammesso che utilizzi lo stesso procedimento di eseguire la divisione mediante una moltiplicazione ed uno shift) prelevi i coefficienti da qualche parte, e che questo prelievo sia leggermente più veloce rispetto a quello che io faccio dagli array globali [inline]v_Q[/inline] e [inline]v_n[/inline].
Concordate sul fatto che anche il compilatore deve avere già a disposizione da qualche parte questi valori? E in tal caso dove?
Molto probabilmente fa semplicemente una divisione intera invece che usare il prodotto e uno shift. In effetti qui puoi vedere che fa quello che dico.
"apatriarca":
Molto probabilmente fa semplicemente una divisione intera invece che usare il prodotto e uno shift. In effetti qui puoi vedere che fa quello che dico.
Per fugare ogni dubbio penso che non mi resti altro che imparare un po' di assembly e vedere il mio compilatore cosa combina nei vari casi.
Ne approfitto per postare la funzione aggiornata:
#define n_B 32
typedef struct d_data_t_
{
uint32_t Q;
unsigned int n_Z;
uint64_t D_max;
} d_data_t;
d_data_t get_d_data_single_value(const uint32_t d)
{
uint32_t Q = 0;
unsigned int n_Z = n_B - 1;
uint64_t D = (uint64_t)1 << n_Z;
uint64_t k_max;
uint64_t D_max;
if(d)
{
for(; !(d & D); --n_Z, D >>= 1);
if(D != d)
{
Q = (D <<= n_B) / d + 1;
k_max = Q / ((uint64_t)Q * d - D);
D_max = (k_max + 1) * (double)D / Q;
}
}
return (d_data_t){Q, n_Z, Q ? D_max : (uint64_t)-1};
}Secondo voi ci sono margini di miglioramento?
Per il calcolo di [inline]k_max[/inline] riesco a cavarmela con una divisione intera, ma per [inline]D_max[/inline], dal momento che quel prodotto può generare un overflow, ho pensato di utilizzare il tipo [inline]double[/inline]. A tal proposito è possibile calcolare [inline]D_max[/inline] senza utilizzare variabili a virgola mobile o soluzioni troppo arzigogolate? E, visto che non ho molta esperienza con l'analisi numerica riguardante i numeri in floating point, mi chiedevo se l'utilizzo di [inline]double[/inline] in questa circostanza potesse riservare qualche "sorpresa" inaspettata.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo