Gruppo fondamentale un po' infame (credo)

[otta96]

Se prendo un toro ($S^1\timesS^1$) e gli tolgo un punto, lo spazio che ottengo che gruppo fondamentale avrà?

[tommy1996q]

Difficile spiegare l'idea, soprattutto senza disegni. Deformi lungo il "cerchio di raggio maggiore" fino ad avere le due parti del toro collegate solo a un punto. I due pezzi che rimangono sopra e sotto possono essere deformati fino a delle circonferenze, e alla fine ti rimane un bouquet di due circonferenze. E' noto (o lo puoi calcolare facilmente con van kampen) che il gruppo fondamentale è $\mathbb{Z} * \mathbb{Z}$

(Il $*$ indica il prodotto libero)

[killing_buddha]

il gruppo fondamentale di una generica superficie $S_g$ di genere $g$ si trova con Van Kampen.

Nel caso specifico il toro si identifica a un quoziente del quadrato $[0,1]^2$ identificando $(x,0)$ con $(x,1)$ e $(0,y)$ con $(1,y)$. Se togli un punto al toro, c'è un retratto di deformazione del toro sul bordo del quadrato, che passa al quoziente come \(S^1 \vee S^1\); a questo punto, \(\pi_1(S^1\vee S^1,x)\cong \mathbb Z * \mathbb Z\) (il gruppo libero su due generatori).

Nel caso generale, fai questo stesso ragionamento usando, invece del quadrato, un $2g$-agono dove i lati opposti vengono identificati a due a due secondo la regola che li orienta (diciamo) in senso orario, sceglie un lato qualsiasi e lo chiama $a_1$, il successivo $b_1$, e i successivi \(a_1^{-1}, b_1^{-1}, a_2, b_2, a_2^{-1}, b_2^{-1},\dots\).

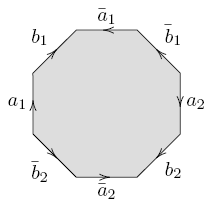
Se ora togli un punto a questa superficie disegnata come $2g$-agono, è facile dimostrare che il suo bordo ne è un retratto di deformazione e dunque deve avere lo stesso gruppo fondamentale.

L'idea geometrica sotto questo fatto, che una dimostrazione pienamente formale usando van Kampen fa emergere, è che la presenza del 2-scheletro di $S_g$ introduce dei commutatori che abelianizzano il gruppo fondamentale di \(S_g \setminus \{p\} = \mathbb Z^{* 2g}\) rendendolo isomorfo a $\mathbb Z^{2g}$ (la somma diretta di gruppi abeliani): scegli come aperti per usare VK un $U$ isomorfo a un disco centrato nel centro $p$ del 2g-agono e un \(V = S_g \setminus\{p\}\); allora, quando calcoli il pushout
\[
\pi_1(S_g) \cong \pi_1(U) *_{\pi_1(U\cap V)} \pi_1(V)
\]
ciò che stai facendo è il quoziente \(\mathbb Z^{ * 2g}/N = F\langle a_i, b_i \mid i=1,...,g\rangle/N\), dove $N$ è il sottogruppo normale generato da
\[
\prod_{i=1}^g [a_i, b_i] = 1
\]

[killing_buddha]

Nota incidentalmente che la domanda che hai fatto tu è la base per dimostrare per induzione su $g$ il risultato: i due aperti di $S_g$ che usi per Van Kampen sono il toro bucato e $S_{g-1}$ bucata. Esse si intersecano in $S^1$, e del resto ciascun cammino in $U\cap V$ è nullomotopo sia in $U$ che in $V$, sicché hai come risultato che \(\pi_n(S_g) \cong \pi_n(S_{g-1}) * \mathbb Z^{* 2}\).

[otta96]

Ma quindi è lo stesso del piano senza due punti?

[killing_buddha]

Quanto ti turba la cosa, in una scala da 0 a "teorema di Whitehead"?

[otta96]

Mi turba di più il fatto che la scala arrivi al "teorema di Whitehead", che non ho assolutamente idea di cosa sia.

[killing_buddha]

La risposta comunque è sì.

Se vuoi imbarcarti nella enorme fatica di trovare una mappa tra il toro bucato e il piano senza due punti che sia un'equivalenza omotopica sei il benvenuto (il teorema di Whitehead è un risultato che dice che questo è possibile quando trovi una mappa in una direzione che induce isomorfismi in tutti i gruppi di omotopia -qui basta il primo: $\pi_{\ge 2}(S^1 \vee S^1)=0$, mi sembra).