Yo-yo

Fai una domanda Tutte le categorie
Steven11
Steven11
22 dic 2006, 17:54
Chiedo di nuovo aiuto per questo esercizio

Uno yo-yo (cilindro pieno) è avvolto da una cordicella.
La sua massa è $m$ e il raggio $R$.
La corda è tenuta fissa e il cilindro cade verticalmente.
Dimostra che il modulo dell'accelerazione del cilindro è $2g/3$
Trovare inoltra la tensione della corda.
ps: il momento di inerzia di un cilindro pieno è $1/2mR^2$
Grazie in anticipo.
Risposte
giuseppe87x
giuseppe87x
22 dic 2006, 17:32
Considera un sistema di riferimento con l'asse $y$ rivolto verso l'alto; si ha:
$sumvecF_(y)=mveca$; $T-mg=ma$
$sumvecM_(z)=Ialpha$; $Tr=-Ialpha$
Poichè $a=alphar$ eliminando $T$ si ha:
$(ma+mg)r=-Ia/r$
$(ma+mg)r^2=-1/2mr^2a$
$a+g=-1/2a$
$a=2/3g$
Steven11
Steven11
22 dic 2006, 21:44
"giuseppe87x":
Considera un sistema di riferimento con l'asse $y$ rivolto verso l'alto; si ha:
$sumvecF_(y)=mveca$; $T-mg=ma$
$sumvecM_(z)=Ialpha$; $Tr=-Ialpha$
Poichè $a=alphar$ eliminando $T$ si ha:
$(ma+mg)r=-Ia/r$
$(ma+mg)r^2=-1/2mr^2a$
$a+g=-1/2a$
$a=2/3g$


Grazie, il fatto è che non capisco perchè nell'eqazione del momento bisogna escludere il momento causato dalla forza peso.
Tu calcoli il momento di T rispetto al centro, che causa una accelerazione verso il basso: ma perchè nella sommatoria dei momenti non si include anche la mg? Se mi chiarissi le idee te ne sarei grato. Ciao
giuseppe87x
giuseppe87x
22 dic 2006, 22:59
Semplice: perchè come polo abbiamo scelto il centro di massa dello yo-yo e come noto il braccio della forza peso rispetto al c.d.m. è nullo.
Eredir
Eredir
22 dic 2006, 23:10
"+Steven+":
Grazie, il fatto è che non capisco perchè nell'eqazione del momento bisogna escludere il momento causato dalla forza peso.
Tu calcoli il momento di T rispetto al centro, che causa una accelerazione verso il basso: ma perchè nella sommatoria dei momenti non si include anche la mg? Se mi chiarissi le idee te ne sarei grato. Ciao




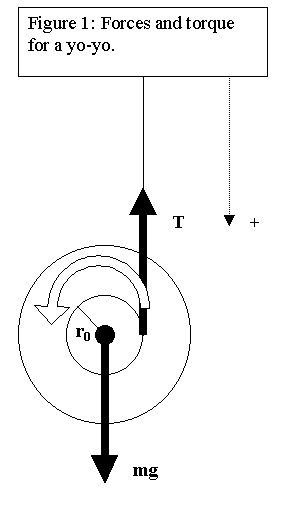
La forza peso è applicata al centro, quindi il braccio risulta nullo e di conseguenza anche il momento.
Steven11
Steven11
23 dic 2006, 10:16
Ok, grazie a entrambi
Ultima domanda: è possibile scegliere un punto diverso dal centro come polo? Ad esempio il punto più a sinistra? Perchè in questo caso bisognerebbe considerare entrambri i momenti... Vorrei sapere se è un procedimento corretto, grazie.
giuseppe87x
giuseppe87x
23 dic 2006, 10:45
E' corretto, i conti tornano lo stesso.
Rispondi
Per rispondere a questa discussione devi prima effettuare il login.