Tre forze e la risultante
Tre forze f1=10N, f2=15N e f3 giacciono nel piano xy della figura. Sapendo che la forza risultante ha modulo 20N ed è parallela all'asse x, calcolare la forza f3(dare modulo e angolo con asse x).
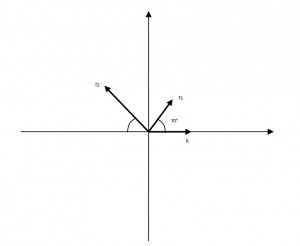
Facendo la regola del parallelogramma f3 dovrebbe trovarsi nel IV quadrante, però viene fuori più un rombo..
Ho provato a fare questi calcoli, ma credo che anche come impostazione siano sbagliati:
$\{(F_(1,x)=F_1costheta),(F_(1,y)=F_1sentheta):}$ $\{(F_(2,x)=F_2cosalpha),(F_(2,y)=F_2senalpha):}$ $\{(F_(3,x)=F_2cosgamma),(F_(2,y)=F_2sengamma):}$
??Primo dubbio, ma le tre forze non dovrebbero essere viste solo in relazione dell'angolo theta?
Grazie mille

Facendo la regola del parallelogramma f3 dovrebbe trovarsi nel IV quadrante, però viene fuori più un rombo..
Ho provato a fare questi calcoli, ma credo che anche come impostazione siano sbagliati:
$\{(F_(1,x)=F_1costheta),(F_(1,y)=F_1sentheta):}$ $\{(F_(2,x)=F_2cosalpha),(F_(2,y)=F_2senalpha):}$ $\{(F_(3,x)=F_2cosgamma),(F_(2,y)=F_2sengamma):}$
??Primo dubbio, ma le tre forze non dovrebbero essere viste solo in relazione dell'angolo theta?
Grazie mille
Risposte
Ciao!
io credevo che un rombo fosse un parallelogramma coi lati uguali, pensa un po'!
Non vedo perché vedere le forze solo in relazione a theta. Finora hai scritto bene (hai solo chiamato l'angolo di F3 gamma, ma fa niente), ognuna delle forze ha il suo angolo rispetto all'asse delle x, a questo punto dovresti sommare le proiezioni su x e porle uguali a 20N e sommare le componenti su y e porle uguali a 0N. In questo modo hai un sistema in due incognite e due equazioni e puoi trovare F3. Cosa non ti torna?
io credevo che un rombo fosse un parallelogramma coi lati uguali, pensa un po'!
Non vedo perché vedere le forze solo in relazione a theta. Finora hai scritto bene (hai solo chiamato l'angolo di F3 gamma, ma fa niente), ognuna delle forze ha il suo angolo rispetto all'asse delle x, a questo punto dovresti sommare le proiezioni su x e porle uguali a 20N e sommare le componenti su y e porle uguali a 0N. In questo modo hai un sistema in due incognite e due equazioni e puoi trovare F3. Cosa non ti torna?
Allora ho provato a fare così:
${\(R_x=F_1costheta+F_2cosbeta+F_3cosgamma), (R_y=F_1sentheta+F_2senbeta+F_3sengamma):}$
${\(20=10cos70+15cos45+F_3cosgamma),(0=10 sen 70+15 sen 45+F_3 sen gamma):}$
${\(5.98=F_3cosgamma), (20=F_3sengamma):}$
mi trovo $(5.98/20=cot gamma) ==> (0.3=cot gamma)$
adesso io non so a che angolo possa corrispondere e anche se una volta saputo, non so in che quadrante si trovi, perchè per esempio l'angolo $beta$ l'ho visto solo dalla figura che è al II quadrante, ma questo metti caso esce di 17 gradi, tanto per dire , io che ne so se sta nel III o IV quad? Per questo ho così tanti dubbi. Spero nel vostro aiuto
${\(R_x=F_1costheta+F_2cosbeta+F_3cosgamma), (R_y=F_1sentheta+F_2senbeta+F_3sengamma):}$
${\(20=10cos70+15cos45+F_3cosgamma),(0=10 sen 70+15 sen 45+F_3 sen gamma):}$
${\(5.98=F_3cosgamma), (20=F_3sengamma):}$
mi trovo $(5.98/20=cot gamma) ==> (0.3=cot gamma)$
adesso io non so a che angolo possa corrispondere e anche se una volta saputo, non so in che quadrante si trovi, perchè per esempio l'angolo $beta$ l'ho visto solo dalla figura che è al II quadrante, ma questo metti caso esce di 17 gradi, tanto per dire , io che ne so se sta nel III o IV quad? Per questo ho così tanti dubbi. Spero nel vostro aiuto
Mi sto imbattendo anche io in questo problema e mi trovo F3sen(teta) = -20 ed F3cos(teta) = 6, poi come si dovrebbe procedere?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo