Tensore di inerzia cilindro
ciao a tutti,
mi servirebbe un aiuto per formalizzare la matrice di inerzia di un cilindro, che ruota attorno all'asse z, con origine del sistema di riferimento NON centrato nel centro di massa.
questa è la matrice di inerzia per un cilindro, con origine del sdr nel centro di massa, rispetto ai 3 assi principali di inerzia:
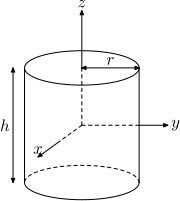
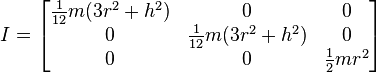
ma per un cilindro come questo? rotazione attorno all'asse z

grazie
mi servirebbe un aiuto per formalizzare la matrice di inerzia di un cilindro, che ruota attorno all'asse z, con origine del sistema di riferimento NON centrato nel centro di massa.
questa è la matrice di inerzia per un cilindro, con origine del sdr nel centro di massa, rispetto ai 3 assi principali di inerzia:

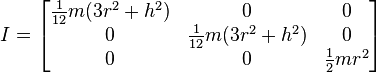
ma per un cilindro come questo? rotazione attorno all'asse z

grazie
Risposte
La terna colorata è principale di inerzia rispetto al centro della base, no? Rotazione intorno all'asse z oppure a un qualunque asse giacente nel piano di base, passante per il centro del cerchio, è la stessa cosa, no ? Ce ne sono infinite, di terne principali con origine in questo centro.
Allora si tratta di applicare il teorema di trasporto.
Allora si tratta di applicare il teorema di trasporto.
"navigatore":
La terna colorata è principale di inerzia rispetto al centro della base, no?
penso di si, l'origine della terna colorata sta nel centro del cerchio di base (lungo l'asse z della prima figura)
"navigatore":
Rotazione intorno all'asse z oppure a un qualunque asse giacente nel piano di base, passante per il centro del cerchio, è la stessa cosa, no ? Ce ne sono infinite, di terne principali con origine in questo centro.
rotazione intorno all'asse z perpendicolare allo schermo
"navigatore":
Allora si tratta di applicare il teorema di trasporto.
del trasporto?? what ?
L' asse z in azzurro, perpendicolare al piano del disegno, è del tutto equivalente all'asse verde y, ai fini del calcolo del momento di inerzia del cilindro. Questo per la simmetria rotazionale del cilindro rispetto all'asse rosso x , che nella prima figura hai chiamato $z$.
Anzi, qualunque asse passante per l'origine delle coordinate colorate e giacente nel piano del cerchio di base è principale di inerzia per tale origine. Ce ne sono infiniti, ovviamente.
Per calcolare il momento di inerzia principale colorato $I_z = I_y$ , prendi quello nero rispetto a y (primo disegno), e aggiungi il termine di trasporto. Sai che cosa è ? Teorema di Huygens.
Anzi, qualunque asse passante per l'origine delle coordinate colorate e giacente nel piano del cerchio di base è principale di inerzia per tale origine. Ce ne sono infiniti, ovviamente.
Per calcolare il momento di inerzia principale colorato $I_z = I_y$ , prendi quello nero rispetto a y (primo disegno), e aggiungi il termine di trasporto. Sai che cosa è ? Teorema di Huygens.
si ok, quindi dovrebbe essere così:
se io centrassi il sistema di riferimento colorato del mio disegno, nel centro di massa del cilindro otterrei:
$I=( ( 1/2mr^2 , 0 , 0 ),( 0 , 1/12m(3r^2+h^2) , 0 ),( 0, 0 , 1/12m(3r^2+h^2)) )$
il teorema di HS o degli assi paralleli dice che:
$ I_o=I_(cdm)+Md^2 $
quindi ottengo:
$ I=( ( 1/2mr^2 , 0 , 0 ),( 0 , 1/12m(3r^2+h^2) , 0 ),( 0, 0 , 1/12m(3r^2+h^2)) )+md^2 $
$ I=( ( 1/2mr^2 +md^2, md^2 , md^2 ),( md^2, 1/12m(3r^2+h^2)+md^2 , md^2 ),( md^2,md^2 , 1/12m(3r^2+h^2)+md^2) ) $
dove $m$ è la massa del cilindro, e $d$ la distanza tra il centro di massa e l'origine del nuovo sistema di riferimento
giusto?
se io centrassi il sistema di riferimento colorato del mio disegno, nel centro di massa del cilindro otterrei:
$I=( ( 1/2mr^2 , 0 , 0 ),( 0 , 1/12m(3r^2+h^2) , 0 ),( 0, 0 , 1/12m(3r^2+h^2)) )$
il teorema di HS o degli assi paralleli dice che:
$ I_o=I_(cdm)+Md^2 $
quindi ottengo:
$ I=( ( 1/2mr^2 , 0 , 0 ),( 0 , 1/12m(3r^2+h^2) , 0 ),( 0, 0 , 1/12m(3r^2+h^2)) )+md^2 $
$ I=( ( 1/2mr^2 +md^2, md^2 , md^2 ),( md^2, 1/12m(3r^2+h^2)+md^2 , md^2 ),( md^2,md^2 , 1/12m(3r^2+h^2)+md^2) ) $
dove $m$ è la massa del cilindro, e $d$ la distanza tra il centro di massa e l'origine del nuovo sistema di riferimento
giusto?

Hai fatto un po' di confusione.
Il teorema degli assi paralleli, o di Huygens, ti consente di dire, con riferimento alla figura con gli assi colorati (origine nel centro del cerchio di base) che :
$I_y = I_z = 1/(12)m(3r^2 + h^2) + m(h/2)^2 = m(r^2/4 + h^2/3) $
Questi due sono momenti principali di inerzia uguali : è sempre lo stesso valore qualunque sia l'asse passante per l'origine detta e giacente nel piano $yz$.
Il terzo momento principale di inerzia, rispetto all'asse x, non cambia affatto, è sempre uguale a : $I_x = 1/2mr^2$. E questo per il semplice motivo che si tratta dello stesso asse che nella prima figura avevi indicato con $z$.
È chiaro?
Essendo i tre assi anzidetti principali di inerzia per il centro del cerchio di base, la matrice è sempre diagonale, gli elementi fuori diagonale sono nulli.
Perciò , ora si può scrivere per bene questa benedetta matrice :
$ I=( ( I_x , 0 , 0 ),( 0, I_y , 0 ),( 0 , 0 , I_z ) )$
ovvero :
$ I=( ( 1/2mr^2 , 0 , 0 ),( 0, m(r^2/4+h^2/3) , 0 ),( 0 , 0 , m(r^2/4+h^2/3)) ) $
Alla fine, ce l'abbiamo fatta….
Il teorema degli assi paralleli, o di Huygens, ti consente di dire, con riferimento alla figura con gli assi colorati (origine nel centro del cerchio di base) che :
$I_y = I_z = 1/(12)m(3r^2 + h^2) + m(h/2)^2 = m(r^2/4 + h^2/3) $
Questi due sono momenti principali di inerzia uguali : è sempre lo stesso valore qualunque sia l'asse passante per l'origine detta e giacente nel piano $yz$.
Il terzo momento principale di inerzia, rispetto all'asse x, non cambia affatto, è sempre uguale a : $I_x = 1/2mr^2$. E questo per il semplice motivo che si tratta dello stesso asse che nella prima figura avevi indicato con $z$.
È chiaro?
Essendo i tre assi anzidetti principali di inerzia per il centro del cerchio di base, la matrice è sempre diagonale, gli elementi fuori diagonale sono nulli.
Perciò , ora si può scrivere per bene questa benedetta matrice :
$ I=( ( I_x , 0 , 0 ),( 0, I_y , 0 ),( 0 , 0 , I_z ) )$
ovvero :
$ I=( ( 1/2mr^2 , 0 , 0 ),( 0, m(r^2/4+h^2/3) , 0 ),( 0 , 0 , m(r^2/4+h^2/3)) ) $
Alla fine, ce l'abbiamo fatta….


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo