Resistenza di un condensatore cilindrico
potreste aiutarmi? ho un condensatore cilindrico di raggi a
ln(b/a) fratto sigma*2*pi*l.... Da dove spunta fuori?!?!
ln(b/a) fratto sigma*2*pi*l.... Da dove spunta fuori?!?!
Risposte
ho provato a calcolare la resistenza con la legge di ohm.. il potenziale $V = (q/2\pi \eps l)ln(b/a)... la corrente i la calcolo come densità di corrente J per Superficie... J= conducibilità per campo elettrico E tra a e b... e come superficie considero prima la sup infinitesima l* dr di cui poi ne faccio l'integrale tra a e b...dove sbaglio?
A me sembra che si possa ragionare in questo modo ....
Il dielettrico è un cilindro cavo con raggio interno $a$, raggio esterno $b$ e altezza $l$, in cui la corrente fluisce radialmente. Per calcolarne la resistenza $R$, lo si divide in elementi di spessore infinitesimo $dr$, e di resistenza $dR$. Ora $dR = rho * (dr)/S = 1/sigma * (dr)/S$. La superficie $S$ è quella laterale di un cilindro con raggio di base $r$ e altezza $l$, cioè $S = 2 * pi * r * l$. Quindi $dR = 1/sigma * (dr)/(2 * pi* r * l)$.
Allora la resistenza è $R=\int_a^b dR = \int_a^b 1/sigma * (dr)/(2 * pi * r * l) = 1/(2 * pi * sigma * l) * \int_a^b 1/r dr = 1/(2 * pi * sigma * l) * ln(b/a)$.
Il dielettrico è un cilindro cavo con raggio interno $a$, raggio esterno $b$ e altezza $l$, in cui la corrente fluisce radialmente. Per calcolarne la resistenza $R$, lo si divide in elementi di spessore infinitesimo $dr$, e di resistenza $dR$. Ora $dR = rho * (dr)/S = 1/sigma * (dr)/S$. La superficie $S$ è quella laterale di un cilindro con raggio di base $r$ e altezza $l$, cioè $S = 2 * pi * r * l$. Quindi $dR = 1/sigma * (dr)/(2 * pi* r * l)$.
Allora la resistenza è $R=\int_a^b dR = \int_a^b 1/sigma * (dr)/(2 * pi * r * l) = 1/(2 * pi * sigma * l) * \int_a^b 1/r dr = 1/(2 * pi * sigma * l) * ln(b/a)$.
ciao chiaraotta, per dici che la corrente fluisce radialmente ? non può scorrere parallelamente all'asse del cilindro?
grazie.
grazie.
grazie caraotta!!!:)
"ooo":
... per dici che la corrente fluisce radialmente ? non può scorrere parallelamente all'asse del cilindro?
grazie.
Un condensatore cilindrico è costituito da due armature cilindriche coassiali fra cui viene applicata una $ddp$.
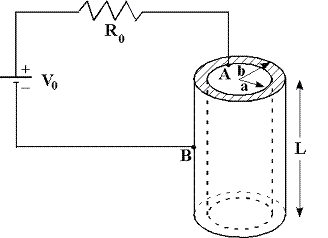
Quindi la corrente passa da una all'altra, e cioè fluisce radialmente.
ok. ma la d.d.p può essere applicata in due modi diversi.
tra le basi opposte del cilindro in modo che la corrente fluisca in modo parallello all'asse ,oppure tra le due superfici interna ed esterna e quindi radialmente come dici tu.
sbaglio qualcosa?
tra le basi opposte del cilindro in modo che la corrente fluisca in modo parallello all'asse ,oppure tra le due superfici interna ed esterna e quindi radialmente come dici tu.
sbaglio qualcosa?
Scusa, ma hai guardato la figura?
si la tua si.ma come fai a sapere di essere in quella circostanza?
l'autore del post non ha precisato nulla a riguardo.
l'autore del post non ha precisato nulla a riguardo.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo