Punto materiale attaccato a filo ruota
Un punto materiale di massa $m=0.35 kg$ attccato adf un filo inestensibile si trova inizialmente nella posizione I. Le viewne impressa una velocità iniziale diretta verso il basso di modulo $5m/s$ ed esso percorre un arco di circonferenza di raggio $R=0.80m$ in un piano verticale . Trascurando gli attriti si determino moduli della velocità del punto e la tensione dle filo nelle posizioni $A$ e $B$
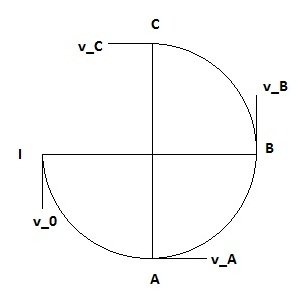
Allora nella Posizione A la forza peso e' ortogonale alla direzione radiale, ma come faccio a calcolarmi la tensione, essa è una forza, quindi mi viene subito da pensare $T=m*a$,dovrei utilizzare il modulo di a, inteso come $sqrt(a_N^2+a_T^2)$?
Però la forza peso non farebbe aumentare la velocità del corpo lungo la circonferenza?
Allora nella Posizione A la forza peso e' ortogonale alla direzione radiale, ma come faccio a calcolarmi la tensione, essa è una forza, quindi mi viene subito da pensare $T=m*a$,dovrei utilizzare il modulo di a, inteso come $sqrt(a_N^2+a_T^2)$?
Però la forza peso non farebbe aumentare la velocità del corpo lungo la circonferenza?
Risposte
Direi che ti conviene usare la conservazione dell'energia (tra l'altro la tensione della fune in questo modo non gioca nessun ruolo perchè è ortogonale allo spostamenti. Puoi calcolarti l'energia potenziale prendendo come riferimento il punto centrale. della circonferenza.
Come detto da newton per calcolarti le velocità usa il principio di conservazione dell'energia meccanica (dato che non ci sono forze esterne che la modifichino).
Quindi $1/2mv_I^2+mgh_I=1/2mv_A^2+mgh_A$ dove $v_I$ è la velocita nel punto $I$, $h_I$ è la quota del punto $I$ misurata da dove vuoi (meglio se usi $I$ o $A$), ecc. Fai lo stesso anche per il punto $B$ (anche se in questo caso non devi calcolare proprio niente ...
).
Per la tensione giustamente parti da $F=ma$ dove $F$ è la tensione ma $a$ è l'accelerazione centripeta e quindi puoi usare la relazione $a_c=v^2/r$ e quindi ... prosegui tu ...
Quindi $1/2mv_I^2+mgh_I=1/2mv_A^2+mgh_A$ dove $v_I$ è la velocita nel punto $I$, $h_I$ è la quota del punto $I$ misurata da dove vuoi (meglio se usi $I$ o $A$), ecc. Fai lo stesso anche per il punto $B$ (anche se in questo caso non devi calcolare proprio niente ...
).Per la tensione giustamente parti da $F=ma$ dove $F$ è la tensione ma $a$ è l'accelerazione centripeta e quindi puoi usare la relazione $a_c=v^2/r$ e quindi ... prosegui tu ...
allora i dubbi sono diversi:
-Stai usando la conservazione dell'energia meccanica perchè è più comoda, ma pur volendo usare le leggi del moto circolare non possiamo calcolarci $a_T$, giusto?
-$1/2 v_I^2=1/2 v_A^2+mgh_A$, il segno dell'altezza h è corretto, pur essendo il punto diretto verso il basso?
-Poi nel calcolo della Tensione T, o onestamente avrei inserito anche la forza peso, che secondo me incide sul moto del punto:
$T=mg+ma_N$, secondo voi è giusto?
-Stai usando la conservazione dell'energia meccanica perchè è più comoda, ma pur volendo usare le leggi del moto circolare non possiamo calcolarci $a_T$, giusto?
-$1/2 v_I^2=1/2 v_A^2+mgh_A$, il segno dell'altezza h è corretto, pur essendo il punto diretto verso il basso?
-Poi nel calcolo della Tensione T, o onestamente avrei inserito anche la forza peso, che secondo me incide sul moto del punto:
$T=mg+ma_N$, secondo voi è giusto?
"75america":
... Stai usando la conservazione dell'energia meccanica perchè è più comoda, ma pur volendo usare le leggi del moto circolare non possiamo calcolarci $a_T$, giusto?
Sì, la uso perché mi torna più comoda, mentre la domanda non l'ho capita ... potresti spiegarti meglio?
"75america":
-$1/2 v_I^2=1/2 v_A^2+mgh_A$, il segno dell'altezza h è corretto, pur essendo il punto diretto verso il basso?
Qui non capisco perché hai dimenticato la massa nel calcolo dell'energia cinetica; poi, finché non sostituisci con i valori togliere dall'espressione di sinistra l'energia potenziale gravitazionale non è corretto; infine l'energia non è un vettore ma uno scalare, idem la quota che quindi non ha verso però ha il segno: se la quota pari a zero l'hai messa dove sta $I$ allora la quota in $A$ è negativa.
"75america":
Poi nel calcolo della Tensione T, o onestamente avrei inserito anche la forza peso, che secondo me incide sul moto del punto:
$T=mg+ma_N$, secondo voi è giusto?
Allora ... $v^2/r=a_c$ quindi dalla velocità e dal raggio ti calcoli l'accelerazione centripeta (e non ci sono dubbi); poi usando questa $F_c=ma_c$ ti calcoli la forza centripeta; ora la forza centripeta è la RISULTANTE delle forze che agiscono sulla massa e quindi, come dici giustamente, sarà la risultante della tensione e della forza peso, e nel caso specifico sarà $F_c=T-mg$.
America il principio di conservazione dell'energia si deriva matematicamente da F=ma! Ogni problema che si risolve con l'energia si risolve anche con Newton! Solo che usando newton compaiono altre incognite (la tensione della fune!) ma alla fine risolvi tutto perchè F=ma è un equazione vettoriale, quindi in realtòà sono 3 equazioni in una!
Nel nostro caso sono 2 equazioni in una perchè il problema è piano
newton dirai senz'altro cose giuste, però quando dici che F=ma è un equazione vettoriale vuol dire che sono presenti vettori, poi sto fatto che dici 3 equazioni in una non lo capisco proprio, guarda ce la sto mettendo tutta per capire, ma le difficoltà non finiscono mai, forse dopo l'esame riprenderò lo studio della fisica a 40 anni, per cercare di capirla come voi
ma voi avete studiato da un solo libro e avete capito tutto?
non avete dubbi se state sbagliando o meno, o sono l'unico pirla che pensa di non capire un ca***
consigliatemi un buon libro di fisica, anche dopo l'esame lo comprerei pur di capirla per bene e saperla spiegare al vostro livello
newton scusa ma mi faresti capire ste due equazioni usando solo F=ma come uscirebbero, così capisco finalmente l'importantza di sto princ. di cons. ener. meccanica, grazie
ma voi avete studiato da un solo libro e avete capito tutto?
non avete dubbi se state sbagliando o meno, o sono l'unico pirla che pensa di non capire un ca***
consigliatemi un buon libro di fisica, anche dopo l'esame lo comprerei pur di capirla per bene e saperla spiegare al vostro livello
newton scusa ma mi faresti capire ste due equazioni usando solo F=ma come uscirebbero, così capisco finalmente l'importantza di sto princ. di cons. ener. meccanica, grazie
"75america":
consigliatemi un buon libro di fisica, anche dopo l'esame lo comprerei pur di capirla per bene e saperla spiegare al vostro livello
Tranquillo, vogliamo solo spiegare ... tu chiedi e noi cerchiamo di farlo ...
Io ti consiglierei l'Halliday-Resnick-ecc. (ce ne sono diverse versioni ...); è vero che navigatore lo odia (
), ma secondo me va bene per imparare i concetti base (in modo sufficientemente rigoroso e con il minimo di matematica necessaria); poi puoi sempre approfondire con migliaia di altri libri ...
axpgn ho provato a completarlo
$1/2 mv_I^2+mgh_I=1/2mv_A^2+mgh_A$
$1/2* 25=1/2 v_A^2+9.8(-0.8)$
$v_A=sqrt[(12.5+7.84)*2]==>v_A=sqrt(40.68)=6.37 m/s$
Tensione filo in A:
$F_C=T_A-mg=m*a_N$
$a_N=v_A^2/R=6.37^2/0.8=50.7 m/s^2$
$T_A=ma_N+mg=0.35*50.7+0.35*9.8=17.75+3.43=21.18N$
In B sempre per la conservazione ener. meccanica:
$1/2mv_A^2+mgh=1/2mv_B^2$ ,però qui ho un problema sempre con l'altezza, se io in $I$ era 0, e in $A$ -R, in $B$ non dovrebbe essere di nuovo 0? O forse mi conviene calcolare secondo un diverso riferimento per tutto?
$1/2 mv_I^2+mgh_I=1/2mv_A^2+mgh_A$
$1/2* 25=1/2 v_A^2+9.8(-0.8)$
$v_A=sqrt[(12.5+7.84)*2]==>v_A=sqrt(40.68)=6.37 m/s$
Tensione filo in A:
$F_C=T_A-mg=m*a_N$
$a_N=v_A^2/R=6.37^2/0.8=50.7 m/s^2$
$T_A=ma_N+mg=0.35*50.7+0.35*9.8=17.75+3.43=21.18N$
In B sempre per la conservazione ener. meccanica:
$1/2mv_A^2+mgh=1/2mv_B^2$ ,però qui ho un problema sempre con l'altezza, se io in $I$ era 0, e in $A$ -R, in $B$ non dovrebbe essere di nuovo 0? O forse mi conviene calcolare secondo un diverso riferimento per tutto?
L'apprendimento è sofferenza! Io stesso per capire certi concetti a volte devo consultare decine di libri diversi! Siamo tutti sulla stessa barca.
Cosa intendo che F=ma è un'equzione vettoriale? F è un vettore, e a è un vettore. m è una costante, ovvero un semplice numero.
Ora ogni vettore si divide (cerco di semplificare il linguaggio) nelle sue componenti.
Un equazione vettoriale è un modo contratto di scrivere 3 equazioni, che sono le seguenti
$F_x = m a_x$
$F_y = m a_y$
$F_z = m a_z$
Ora in questo caso il problema è bidimensionale (ha solo 2 dimensioni) per cui bastano la 1 e la 2 per descrivere il tuo problema.
Cosa intendo che F=ma è un'equzione vettoriale? F è un vettore, e a è un vettore. m è una costante, ovvero un semplice numero.
Ora ogni vettore si divide (cerco di semplificare il linguaggio) nelle sue componenti.
Un equazione vettoriale è un modo contratto di scrivere 3 equazioni, che sono le seguenti
$F_x = m a_x$
$F_y = m a_y$
$F_z = m a_z$
Ora in questo caso il problema è bidimensionale (ha solo 2 dimensioni) per cui bastano la 1 e la 2 per descrivere il tuo problema.
Esplicito meglio il concetto: stai uguagliando il vettore F con il vettore m a. Quando due vettori sono uguali? Sono uguali se e solo se solo se sono uguali le proiezioni sui vari assi. Ovvero se proietto F sull'asse x, e ma sull'asse x, devo ottenere lo stesso numero. Ovvero $F_x = m a_x$. Lo stesso ragionamento lo fai proiettando sull'asse y sull'asse z. Spero che ora ti sia più chiaro.
I dati mi sembrano corretti (l'accelerazione mi sembra alta ma i calcoli mi tornano ...)
In B non devi fare nessun calcolo: essendo alla stessa quota le due energie potenziali sono le stesse quindi puoi eliminarle dall'equazione; ti rimangono le energie cinetiche, dove però la massa è la stessa e quindi ... le velocità sono le stesse.
Chiaro?
"75america":
In B sempre per la conservazione ener. meccanica:
$1/2mv_A^2+mgh=1/2mv_B^2$ ,però qui ho un problema sempre con l'altezza, se io in $I$ era 0, e in $A$ -R, in $B$ non dovrebbe essere di nuovo 0? O forse mi conviene calcolare secondo un diverso riferimento per tutto?
In B non devi fare nessun calcolo: essendo alla stessa quota le due energie potenziali sono le stesse quindi puoi eliminarle dall'equazione; ti rimangono le energie cinetiche, dove però la massa è la stessa e quindi ... le velocità sono le stesse.
Chiaro?
"newton_1372":
Esplicito meglio il concetto: stai uguagliando il vettore F con il vettore m a. Quando due vettori sono uguali? Sono uguali se e solo se solo se sono uguali le proiezioni sui vari assi. Ovvero se proietto F sull'asse x, e ma sull'asse x, devo ottenere lo stesso numero. Ovvero $F_x = m a_x$. Lo stesso ragionamento lo fai proiettando sull'asse y sull'asse z. Spero che ora ti sia più chiaro.
tt chiaro, quindi devo vedere se F sull'asse x mi da un numero $m*a_x$ mi deve dare lo stesso numero, ci fosse scritto così chiaro sui libri, cmq ho anche l'Halliday, io per esempio lavoro, energia sono scalari, però sul libro non c'è una sorta di elenco con vettori e scalari, anche per rendere più semplice la cosa
axpgn allora io per come me l'ero calcolato a B l'altezza diventava di nuovo 0, quindi mi trovavo la stessa velocità, così avrei fatto se stavo da solo all'esame, te dici essendo alla stessa quota, spero tu intenda $I$ e $B$, poi che hanno le stesse energie potenziali a dire il vero non l'ho capita, l'energia potenziale non è $mgh$?
cmq l'ho completato secondo me:
in B, $v_B=v_A$
$T_B=ma_N$ con $a_N=v_B^2/R=50.7 m/s^2$
$T_B=0.35*50.7=17.7N$
cmq l'ho completato secondo me:
in B, $v_B=v_A$
$T_B=ma_N$ con $a_N=v_B^2/R=50.7 m/s^2$
$T_B=0.35*50.7=17.7N$
Più o meno stiamo dicendo la stessa cosa ..
Sì, intendo $I$ e $B$; a quelle quote le energie potenziali sono le stesse perché la massa è la stessa e le quote sono le stesse (da qualunque livello tu le misuri), quindi i prodotti $mgh$ saranno uguali.
Sì, intendo $I$ e $B$; a quelle quote le energie potenziali sono le stesse perché la massa è la stessa e le quote sono le stesse (da qualunque livello tu le misuri), quindi i prodotti $mgh$ saranno uguali.
allora ho sbagliato, vuol dire che in B c'era la stessa velocità di $I$
ma allora in B che equazione della cons. dell'energia meccanica dovevo scrivere?
e se tale equazione l'avessi fatta partire da $A$ verso $B$ sarebbe stata corretta?
ma allora in B che equazione della cons. dell'energia meccanica dovevo scrivere?
e se tale equazione l'avessi fatta partire da $A$ verso $B$ sarebbe stata corretta?
"75america":
allora ho sbagliato, vuol dire che in B c'era la stessa velocità di $I$
Sì.
Non mi ero accorto che avevi scritto una cosa diversa.
"75america":
ma allora in B che equazione della cons. dell'energia meccanica dovevo scrivere?
Sempre la stessa: "energia cinetica + energia potenziale"; ma, senza fare calcoli, si vede che l'energia potenziale è la stessa in entrambe le situazioni (in $I$ e in $B$) e quindi anche le energie cinetiche sono uguali, e dato che la massa è la stessa anche le velocità saranno uguali
"75america":
e se tale equazione l'avessi fatta partire da $A$ verso $B$ sarebbe stata corretta?
Puoi spiegarti meglio? Non ho capito ...
allora per capire: l'energia potenziale in $B$ è $mgh$?
quindi $a_NB=v_0^2/R=25/0.8=31.25m/s^2$
quindi la $T_B=m*a_N=0.35*31.25$
poi dicevo perchè devo misurare la conservazione dell'energia meccanica dal punto iniziale $I$ e non anche da $A$ volendo, non si poteva fare, cioè mi spiego valeva questa legge:
$1/2mv_A+mgh=1/2mv_B+mgh$?
quindi $a_NB=v_0^2/R=25/0.8=31.25m/s^2$
quindi la $T_B=m*a_N=0.35*31.25$
poi dicevo perchè devo misurare la conservazione dell'energia meccanica dal punto iniziale $I$ e non anche da $A$ volendo, non si poteva fare, cioè mi spiego valeva questa legge:
$1/2mv_A+mgh=1/2mv_B+mgh$?
Dato che non ci sono forze esterne che agiscono sul sistema e abbiamo solo forze conservative, l'energia meccanica si conserva, quindi puoi benissimo usare quella formula (nella quale però c'è un errore: le quote di $A$ e $B$ sono DIVERSE, quindi non puoi indicarle entrambe con la stesso nome, nello specifico $h$, chiamale per esempio $h_a$ e $h_b$).
MA ... come spiegato prima, con un pochino di logica si vede subito che le energie potenziali gravitazionali sono uguali (per lo stesso corpo l'unica variabile in $mgh$ è la quota, e se la quota è la stessa anche il prodotto sarà lo stesso), quindi stessa energia cinetica e perciò stessa velocità.
Se è vero che prendere una qualsiasi tra le strade giuste, va sempre bene, è altrettanto vero però che se prendi quella più corta e più facile è sicuramente meglio; eviti fatica e soprattutto errori.
Cordialmente, Alex
MA ... come spiegato prima, con un pochino di logica si vede subito che le energie potenziali gravitazionali sono uguali (per lo stesso corpo l'unica variabile in $mgh$ è la quota, e se la quota è la stessa anche il prodotto sarà lo stesso), quindi stessa energia cinetica e perciò stessa velocità.
Se è vero che prendere una qualsiasi tra le strade giuste, va sempre bene, è altrettanto vero però che se prendi quella più corta e più facile è sicuramente meglio
; eviti fatica e soprattutto errori.Cordialmente, Alex
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo