Proiettile sparato che colpisce altopiano
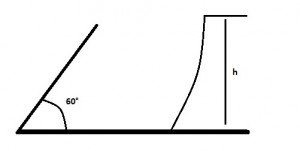
Un proiettile è sparato con velocità iniziale di 36 m/s ed angolo con l'orizzontale di 60° veros un altopiano di altezza h sopra la quota di lancio. Il proiettile colpisce l'altopiano 5 s dopo il lancio. Calcolare: a) l'altezza h dell'altopiano; b) la velocità del proiettile all'impatto; c) la massima altezza raggiunta.
a) $h=v_0senthetat-1/2 g t^2=36sen60 *5-4.9*25=36*0.866*5-122.5=155.28-122.5=33.4 m$
b)$v_x=v_0costheta=36cos60°=36*0.5=18 m/s$
$v_y=v_0sentheta-gt=36*0.866-49=31.176-49=-17.82 m/s$ (È corretto scrivere la velocità negativa?)
$v=sqrt(v_x^2+v_y^2)=sqrt(641,55)=25,32m/s$
c)$y_m=(v_0sen^2theta)/(2g)=(36^2sen^2 60)/19.6=(1296*0.75)/19.6=49.6m$
Scusate ma su questo punto ho una domanda, ma se il punto va a sbattere a $33.4m$ di altezza per l'impatto con l'altopiano
come fa ad arrivare a 49,6m, dopo i 33,4 non dovrebbe scendere?
Io ho provato a risolverlo, secondo voi è corretto?
Grazie sempre,lo dico davvero
a) $h=v_0senthetat-1/2 g t^2=36sen60 *5-4.9*25=36*0.866*5-122.5=155.28-122.5=33.4 m$
b)$v_x=v_0costheta=36cos60°=36*0.5=18 m/s$
$v_y=v_0sentheta-gt=36*0.866-49=31.176-49=-17.82 m/s$ (È corretto scrivere la velocità negativa?)
$v=sqrt(v_x^2+v_y^2)=sqrt(641,55)=25,32m/s$
c)$y_m=(v_0sen^2theta)/(2g)=(36^2sen^2 60)/19.6=(1296*0.75)/19.6=49.6m$
Scusate ma su questo punto ho una domanda, ma se il punto va a sbattere a $33.4m$ di altezza per l'impatto con l'altopiano
come fa ad arrivare a 49,6m, dopo i 33,4 non dovrebbe scendere?
Io ho provato a risolverlo, secondo voi è corretto?
Grazie sempre,lo dico davvero
Risposte
"75america":
Scusate ma su questo punto ho una domanda, ma se il punto va a sbattere a $33.4m$ di altezza per l'impatto con l'altopiano come fa ad arrivare a 49,6m, dopo i 33,4 non dovrebbe scendere?
Io ho provato a risolverlo, secondo voi è corretto?
Grazie sempre,lo dico davvero
Non ho verificato i conti ma, ad occhio, il procedimento sembra corretto.
Il fatto che il punto di atterraggio sia più in basso (e con velocità verticale negativa) significa solo che lo incontra in caduta (dopo esser salito più in alto) e non in fase di salita.
Se tracci la parabola (che trovi con la prima espressione che hai scritto lasciando $t$ come variabile) lo vedi chiaramente
Cordialmente, Alex
Salve!
Scusatemi ho capito il procedimento ma solitamente per calcolare la velocità d'impatto usavo la formula $ sqrt(2gh) $ con h=max altezza raggiunta. Come risultato sarebbe molto vicino a quello ottenuto calcolando le componenti della velocità e il modulo ma non capisco quando usare l'una e quando usare l'altra, potreste aiutarmi? Grazie mille
Scusatemi ho capito il procedimento ma solitamente per calcolare la velocità d'impatto usavo la formula $ sqrt(2gh) $ con h=max altezza raggiunta. Come risultato sarebbe molto vicino a quello ottenuto calcolando le componenti della velocità e il modulo ma non capisco quando usare l'una e quando usare l'altra, potreste aiutarmi? Grazie mille
Quella formula è corretta solo se tutta l'energia cinetica iniziale si trasforma in energia potenziale, cioè se il corpo raggiunge quella data altezza a velocità nulla, il che nel problema in questione non è.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo