Problema tubicino in rotazione con pallina che scorre
Salve a tutti Sto studiando il moto rototraslatorio e mi sono trovato davanti a questo problema che non riesco a risolvere, ve lo rescrivo sperando di poter ricevere un aiuto.
Un tubicino di lunghezza l=20cm può ruotare in un piano orizzontale attarno ad un'asse verticale liscio passante per una sua estremità. Entro il tubicino a metà lunghezza si trova in quiete una sferetta di massa m=20gr il tubicino viene messo in moto con velocità angolare pari a 4rad/s. l'attrito tra la sfera e il tubicino è trascurabile perciò scivola senza rotolare lungo il tubicino.
Si determini il modulo v della velocità della pallina quando esce dal tubicino sapendo che il momento di inerzia I del tubicino è 16Kgcm^2
(scusate ma ancora non ho imparato a inserire i vari simboli quindi perdonatemi le imprecisioni).
Io pensavo di sfruttare il principio di conservazione dell'energia considerando che non agiscono forze esterne ma così facendo non mi torna. io ho presupposto che l'energia cinetica rotazionale iniziale sia uguale a quella finale un'istante prima che la pallina esca ma mia sa che sto sbagliando qualcosa.
Qualcuno è in grado di aiutarmi???
Grazie anticipatamente a tutti
Redbaron990
Un tubicino di lunghezza l=20cm può ruotare in un piano orizzontale attarno ad un'asse verticale liscio passante per una sua estremità. Entro il tubicino a metà lunghezza si trova in quiete una sferetta di massa m=20gr il tubicino viene messo in moto con velocità angolare pari a 4rad/s. l'attrito tra la sfera e il tubicino è trascurabile perciò scivola senza rotolare lungo il tubicino.
Si determini il modulo v della velocità della pallina quando esce dal tubicino sapendo che il momento di inerzia I del tubicino è 16Kgcm^2
(scusate ma ancora non ho imparato a inserire i vari simboli quindi perdonatemi le imprecisioni).
Io pensavo di sfruttare il principio di conservazione dell'energia considerando che non agiscono forze esterne ma così facendo non mi torna. io ho presupposto che l'energia cinetica rotazionale iniziale sia uguale a quella finale un'istante prima che la pallina esca ma mia sa che sto sbagliando qualcosa.
Qualcuno è in grado di aiutarmi???
Grazie anticipatamente a tutti
Redbaron990
Risposte
Non e' tutto chiarissimo...
Se il tubo ruota a velocita' costante allora dell'inerzia del tubo non ce ne facciamo niente.
Se cosi' e', si deve ragionare in termini di coordinate polari.
L'accelerazione in coordinate polari e' espressa da queste formule:
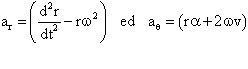
Devi immaginare cosa succede alla pallina nel tubo, a quali forze e' soggetta.....
Se il tubo ruota a velocita' costante allora dell'inerzia del tubo non ce ne facciamo niente.
Se cosi' e', si deve ragionare in termini di coordinate polari.
L'accelerazione in coordinate polari e' espressa da queste formule:
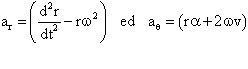
Devi immaginare cosa succede alla pallina nel tubo, a quali forze e' soggetta.....
In effetti il problema come è scritto non è chiarissimo, in particolare non è chiaro cosa significhi che "il tubicino viene messo in moto con velocità angolare pari a 4rad/s"...
Se si intende che tutto il sistema è messo in moto e poi mantiene una velocità di rotazione costante e che la massa all'inizio ha velocità nulla rispetto al tubo, allora la maniera più semplice per risolverlo, senza la necessità di passare alle coordinate polari, è quello di mettersi in un sistema di riferimento solidale col tubicino e vedere le forze apparenti che agiscono sulla massa: la forza centrifuga e la forza di Coriolis.
La forza di Coriolis non compie lavoro nel sistema di riferimento solidale perché tale forza è perpendicolare allo spostamento relativo , mentre il lavoro della forza centrifuga è calcolabile da un integrale semplice.....
Tale lavoro sarà uguale alla variazione di energia cinetica nel sistema solidale. Nota quindi questa è nota la velocità della sfera alla fine rispetto al riferimento solidale e quindi si può calcolare la velocità della massa all'uscita (somma della velocità radiale relativa e di quella di trascinamento tangenziale).
C'è da osservare che affinché la velocità di rotazione sia costante occorrerebbe applicare un momento esterno al sistema, momento calcolabile....
Comunque se non si è interessati al calcolo di tale momento in effetti il dato sull'inerzia del tubo è inutile.
Se invece si intende che una volta in moto non è applicato al sistema alcun momento esterno allora le cose sono diverse.
Basta osservare in tal caso che non essendo applicati momenti esterni il momento angolare totale deve conservarsi, inoltre sul sistema non agiscono forze né momenti che compiono lavoro per cui anche l'energia cinetica deve conservarsi.
Dalla prima conservazione si ottiene la velocità angolare finale, mentre dalla seconda si può ottenere la velocità finale della massa.
Se si intende che tutto il sistema è messo in moto e poi mantiene una velocità di rotazione costante e che la massa all'inizio ha velocità nulla rispetto al tubo, allora la maniera più semplice per risolverlo, senza la necessità di passare alle coordinate polari, è quello di mettersi in un sistema di riferimento solidale col tubicino e vedere le forze apparenti che agiscono sulla massa: la forza centrifuga e la forza di Coriolis.
La forza di Coriolis non compie lavoro nel sistema di riferimento solidale perché tale forza è perpendicolare allo spostamento relativo , mentre il lavoro della forza centrifuga è calcolabile da un integrale semplice.....
Tale lavoro sarà uguale alla variazione di energia cinetica nel sistema solidale. Nota quindi questa è nota la velocità della sfera alla fine rispetto al riferimento solidale e quindi si può calcolare la velocità della massa all'uscita (somma della velocità radiale relativa e di quella di trascinamento tangenziale).
C'è da osservare che affinché la velocità di rotazione sia costante occorrerebbe applicare un momento esterno al sistema, momento calcolabile....
Comunque se non si è interessati al calcolo di tale momento in effetti il dato sull'inerzia del tubo è inutile.
Se invece si intende che una volta in moto non è applicato al sistema alcun momento esterno allora le cose sono diverse.
Basta osservare in tal caso che non essendo applicati momenti esterni il momento angolare totale deve conservarsi, inoltre sul sistema non agiscono forze né momenti che compiono lavoro per cui anche l'energia cinetica deve conservarsi.
Dalla prima conservazione si ottiene la velocità angolare finale, mentre dalla seconda si può ottenere la velocità finale della massa.
Propendo per la seconda interpretazione. Forse serve anche una relazione cinematica per cui la velocità relativa di uscita deve essere radiale...
Si anche io immagino che il caso sia il secondo considerando che dice viene messo in moto a velocità 4rad/s e non che mantiene quella velocità ma io ho provato a fare come suggerisce Faussone ma non mi torna il risultato provo a scrivere qui di sotto le equazioni che ho impostato se trovate degli errori correggetemi.
Conservazione della quantità di moto:
$(I+(l^2)m/4)omegao = (I+(l^2)m)omegaf $
Conservazione dell'energia:
$(I+(l^2)m/4)omegao^2 = (I+(l^2)m)omegaf^2 + m(Vrad)^2$
Dove $omega0$ e $omegaf$ sono rispettivamente velocità angolare iniziale e finale del sistema e $Vrad$ è la velocità radiale della pallina quando esce dal tubo.
è giusto presupporre che la pallina all'istante di partenza ha velocità radiale 0?
Va bene ho c'è qualcosa che manca perchè se non erro risolvendo il sistema poi dovrei fare il modulo sommado sotto radice i quadrati della velocità tangenziale e di quella radiale della pallina giusto?
Io ho provato a fare i calcoli ma non mi tornano.
Se per caso qualcuno volesse provare il risultato che da il libro è il seguente:
$v= (omega0 l)/(2(I+ml^2)) sqrt(7I^2+23/4Iml^2+m^2l^4) =1,07m/s$
Spero di essere stato chiaro e di aver scritto tutto bene
Grazie mille a tutti
Spero possiate aiutarmi
Conservazione della quantità di moto:
$(I+(l^2)m/4)omegao = (I+(l^2)m)omegaf $
Conservazione dell'energia:
$(I+(l^2)m/4)omegao^2 = (I+(l^2)m)omegaf^2 + m(Vrad)^2$
Dove $omega0$ e $omegaf$ sono rispettivamente velocità angolare iniziale e finale del sistema e $Vrad$ è la velocità radiale della pallina quando esce dal tubo.
è giusto presupporre che la pallina all'istante di partenza ha velocità radiale 0?
Va bene ho c'è qualcosa che manca perchè se non erro risolvendo il sistema poi dovrei fare il modulo sommado sotto radice i quadrati della velocità tangenziale e di quella radiale della pallina giusto?
Io ho provato a fare i calcoli ma non mi tornano.
Se per caso qualcuno volesse provare il risultato che da il libro è il seguente:
$v= (omega0 l)/(2(I+ml^2)) sqrt(7I^2+23/4Iml^2+m^2l^4) =1,07m/s$
Spero di essere stato chiaro e di aver scritto tutto bene
Grazie mille a tutti
Spero possiate aiutarmi
Le equazioni che hai scritto sono corrette.
E anche il risultato riportato dal libro coincide con quello che troveresti usando quelle equazioni (te lo dico perché l'ho verificato ).
).
Devi ricordarti che alla fine la velocità della sferetta sarà $sqrt((omega_f*l)^2 + v_r^2)$.
Poi il resto sono solo conti...
E anche il risultato riportato dal libro coincide con quello che troveresti usando quelle equazioni (te lo dico perché l'ho verificato
 ).
).Devi ricordarti che alla fine la velocità della sferetta sarà $sqrt((omega_f*l)^2 + v_r^2)$.
Poi il resto sono solo conti...
Ok grazie mille torna avevo fatto un gran casino con i calcoli ma alla fine dopo diversi tentativi sono riuscito a far tornare il tutto.
Grazie mille mi siete stati veramente di grande aiuto
A presto
Redbaron990
Grazie mille mi siete stati veramente di grande aiuto
A presto
Redbaron990
Perdonate la domanda stupida, ma come si giustifica che nel primo caso si compie un moto rettilineo uniforme?
Inoltre ho veramente le idee confuse in fisica, come mai se non ci sono forze agenti sulla sferetta nel sistema solidale questa modifica la sua velocità?
Inoltre ho veramente le idee confuse in fisica, come mai se non ci sono forze agenti sulla sferetta nel sistema solidale questa modifica la sua velocità?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo