Pendolo oscillante all'interno di un carrello
Ciao a tutti, ho difficoltà a capire come ottenere la forma i-s-u corretta del seguente modello:
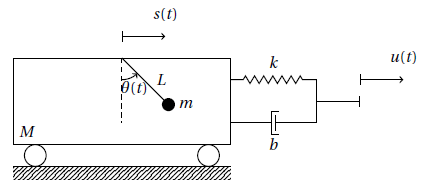
Pendolo all'interno del carrello:
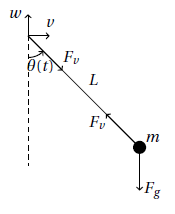
Se indichiamo con $(v_m(t),w_m(t))$ la posizione della massa del pendolo, come faccio a mettere in relazione le due componenti con $s(t)$?
Le due relazioni dovrebbero essere queste:
$v_m(t)=s(t)+Lsin\theta(t)$
$w_m(t)=-Lcos\theta(t)$
Il fatto è che non capisco perchè.
Per $v_m(t)$, non basta considerare la sua proiezione traslata a sinistra ed ottenere $v_m(t)=Lsin\theta(t)$? Cosa che invece vale per $w_m(t)$, ma il segno meno come può essere giustificato?

Pendolo all'interno del carrello:

Se indichiamo con $(v_m(t),w_m(t))$ la posizione della massa del pendolo, come faccio a mettere in relazione le due componenti con $s(t)$?
Le due relazioni dovrebbero essere queste:
$v_m(t)=s(t)+Lsin\theta(t)$
$w_m(t)=-Lcos\theta(t)$
Il fatto è che non capisco perchè.
Per $v_m(t)$, non basta considerare la sua proiezione traslata a sinistra ed ottenere $v_m(t)=Lsin\theta(t)$? Cosa che invece vale per $w_m(t)$, ma il segno meno come può essere giustificato?
Risposte
Se tu sei su una banchina di una ferrovia e hai un treno davanti a te che comincia a muoversi e una persona che comincia a camminare all'interno del treno (nella stessa direzione, supponiamo), secondo te, per misurare la sua coordinata rispetto alla banchina, come devi agire? Dovrai misurare la coordinata di un punto del treno (la coda, per esempio) e poi aggiungere la distanza a cui si trova il tizio dalla coda stessa del treno.
Qui e' analogo: la coordinata orizzontale della sfera rispetto al sistema di riferimento fisso e' pari alla somma della coordinata orizzontale del punto di attacco del pendolo al soffitto $s(t)$, piu la distanza (orizzontale) che la sfera ha rispetto al punto di attacco $Lsintheta$.
Per la verticale, stessa cosa. Se metti l'origine di y nel punto di attacco, la distanza del punto di attacco e' nulla. Ti resta da aggiungere a 0 la distanza della pallina (in verticale), che e' $-Lcostheta$. Il segno meno tiene conto del fatto che la y e' orientata, arbitrariamente, verso l'alto.
Qui e' analogo: la coordinata orizzontale della sfera rispetto al sistema di riferimento fisso e' pari alla somma della coordinata orizzontale del punto di attacco del pendolo al soffitto $s(t)$, piu la distanza (orizzontale) che la sfera ha rispetto al punto di attacco $Lsintheta$.
Per la verticale, stessa cosa. Se metti l'origine di y nel punto di attacco, la distanza del punto di attacco e' nulla. Ti resta da aggiungere a 0 la distanza della pallina (in verticale), che e' $-Lcostheta$. Il segno meno tiene conto del fatto che la y e' orientata, arbitrariamente, verso l'alto.
Le due componenti della massa non sono queste?
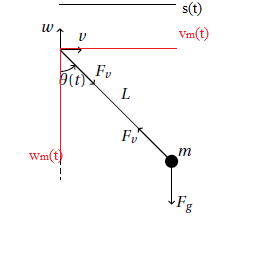

Si. A quella orizzontale devi aggiungere anche la coordinata orizzontale del punto di attacco del pendolo.
Altrimenti quelle sono le coordinate che ti darebbe un osservatore che sta dentro carrello.
Altrimenti quelle sono le coordinate che ti darebbe un osservatore che sta dentro carrello.
Disegnate in quel modo però non mi trovo, $s(t)$ è più corta rispetto a $v_m(t)$? Sto cercando di risolvere il problema per via geometrica.
A quella orizzontale devi aggiungere anche la coordinata orizzontale del punto di attacco del pendolo.
Non riesco a capire cosa manca nel disegno...
Se $s(t)$ mi indica la posizione del carrello e $v_m(t)$ la posizione del pendolo rispetto al sistema di riferimento fisso che ha origine nel punto di attacco del pendolo nel carrello, non dovrei considerare i due casi in cui $v_m(t)$ è minore, uguale o maggiore di $s(t)$?
Tra l'altro sul testo è scritto che $v_m(t)^2+w_m(t)^2=L^2$
E che ne so che devi fare?
La descrizione dell'ascissa assoluta del pendolo e' quella: poi quello che devi trovare lo sai tu in base a quello che ti chiede l'esercizio
La descrizione dell'ascissa assoluta del pendolo e' quella: poi quello che devi trovare lo sai tu in base a quello che ti chiede l'esercizio
Devo semplicemente trovare il modello i-s-u, il fatto è che non capisco quel passaggio che ho spiegato nel primo post.
Io dal disegno fornito nel testo vedo graficamente che $s(t)=v_m(t)$, ma a quanto ho capito ciò è concettualmente sbagliato e vorrei capirne il motivo.
Io dal disegno fornito nel testo vedo graficamente che $s(t)=v_m(t)$, ma a quanto ho capito ciò è concettualmente sbagliato e vorrei capirne il motivo.
Scusa l'ignoranza, ma cosa e' il modello isu? E poi vedi che graficamente s (t) = a cosa?
"professorkappa":
Scusa l'ignoranza, ma cosa e' il modello isu? E poi vedi che graficamente s (t) = a cosa?
modello ingresso-stato-uscita, mi confermi che $s(t)$ mi indica la distanza del punto di riferimento rispetto al centro di massa del carrello? Se così fosse allora mi è tutto chiaro sulla componente orizzontale.
Ho ancora dei dubbi sulla componente verticale, se avessi deciso di prendere il sistema di riferimento $vm$ con le $w$ in verso opposto alla figura che ho postato, cosa sarebbe cambiato?
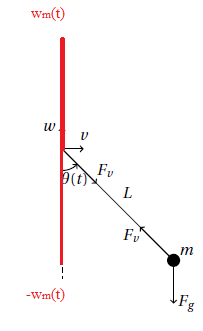
È corretto? È questo che giustifica il segno meno?
PS: $w_m(t)$ è il vettore in rosso più doppio.
Non so cosa intendi.
La proiezione della posizione massa m sull'asse verticale e', in modulo, $Lcostheta$.
Siccome tale proiezione cade nel semiasse negativo, perche l'origine e' posta nel punto inferiore del vettore rosso doppio, devi metterci un meno davanti.
L'esercizio mi sembra avanzato: com'e' possibile che tu ancora abbia dubbi e confusione e identificare la posizione di un corpo nel piano?
La proiezione della posizione massa m sull'asse verticale e', in modulo, $Lcostheta$.
Siccome tale proiezione cade nel semiasse negativo, perche l'origine e' posta nel punto inferiore del vettore rosso doppio, devi metterci un meno davanti.
L'esercizio mi sembra avanzato: com'e' possibile che tu ancora abbia dubbi e confusione e identificare la posizione di un corpo nel piano?
Grazie per l'aiuto e per la pazienza, è da anni che non tocco la Fisica 


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo