Non mi torna il momento di inerzia del cono.
Ho provato a ricavare il momento di inerzia del cono PIENO, applicando la definizione ma mi sbaglio sempre di un fattore 2. Il cono deve avere (3/10)Mr^2. Io però voglio capire da dove deve saltare fuori quel (1/2) mancante. Sono 4 giorni che ci impreco sopra senza risultati. E sì, lo so che i dischi hanno il momento di 1/2Mr^2 nel caso vogliate scriverlo, ma il mio punto è che 1/2 qui non mi appare applicando i procedimenti dove ottengo il volume infinitesimo e la massa infinitesima. Io non voglio sapere che il disco ha la metà del prodotto tra il quadrato del raggio e la massa perché io non ho nemmeno pensato di integrare a dischi. Voglio sapere dove sbaglio algebricamente perché sto problema mi sta facendo dire l'indicibile.
Ringrazio per l'eventuale aiuto.
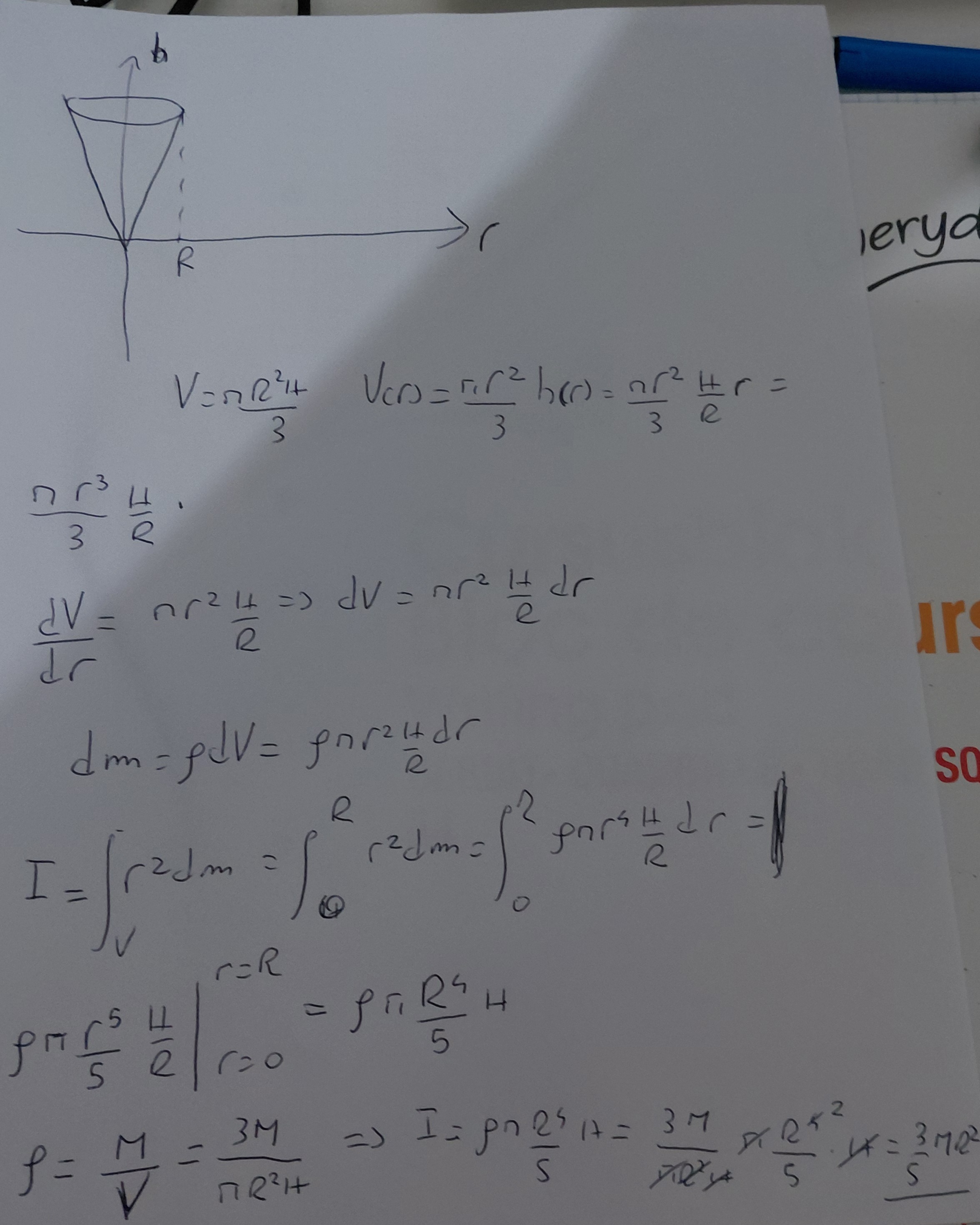
Ringrazio per l'eventuale aiuto.
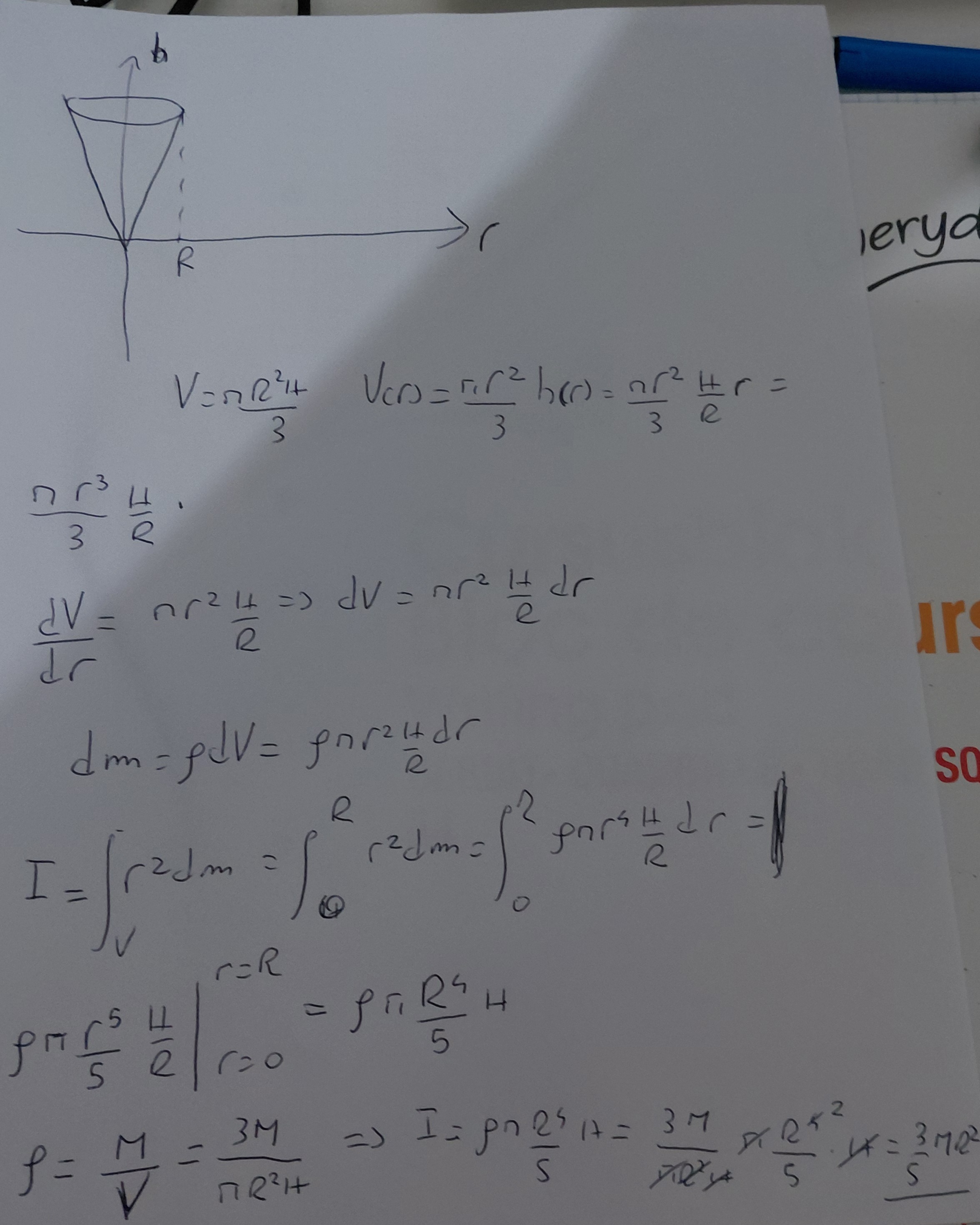
Risposte
Credo che ci sia un problema di fondo, ovvero che la relazione z=r*H/R va interpretata come limite di integrazione e non sostituita banalmente nella formula del volume, perchè è una relazione valida solo sulla superficie laterale del cono. In particolare scritta come r=R*z/H ci dice che per ogni z l'integrazione per la r va estesa da 0 a R*z/H.
Quindi se si vuole applicare la definizione ovvero fare l'integrale sul volume si useranno le coordinate cilindriche per le quali risulta
dV=r dr dθ dz
e l'integrazione per il momento d'inerzia sarà data dall'integrale triplo
Nell'ordine prima si integrerà in θ, poi in r e infine in z.
Quindi se si vuole applicare la definizione ovvero fare l'integrale sul volume si useranno le coordinate cilindriche per le quali risulta
dV=r dr dθ dz
e l'integrazione per il momento d'inerzia sarà data dall'integrale triplo
[math]\int_0^{H}\int_0^{Rz/H} \int_0^{2\pi} \rho\ r^3 dz dr d\theta[/math]
Nell'ordine prima si integrerà in θ, poi in r e infine in z.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo