Moto circolare con filo in tensione
Ciao a tutti. Ho difficoltà nel risolvere il seguente esercizio:
Un punto materiale è vincolato a muoversi in un piano orizzontale con attrito. Il coefficiente di attrito dinamico u è pari a 0.1. Il punto materiale è collegato ad un filo di lunghezza L=7m e ruota rispetto ad un punto fisso O. Il filo è in grado di sostenere una tensione massima pari a Tmax=10 N. Si immagini di aumentare progressivamente la velocità di rotazione del punto materiale. Ad un certo istante il filo si spezza ed il punto materiale percorre una distanza pari a d=7 m (Calcolata rispetto al punto di rilascio) prima di fermarsi.
Quanto vale la massa del punto materiale?
Ho schematizzato banalmente in questo modo:
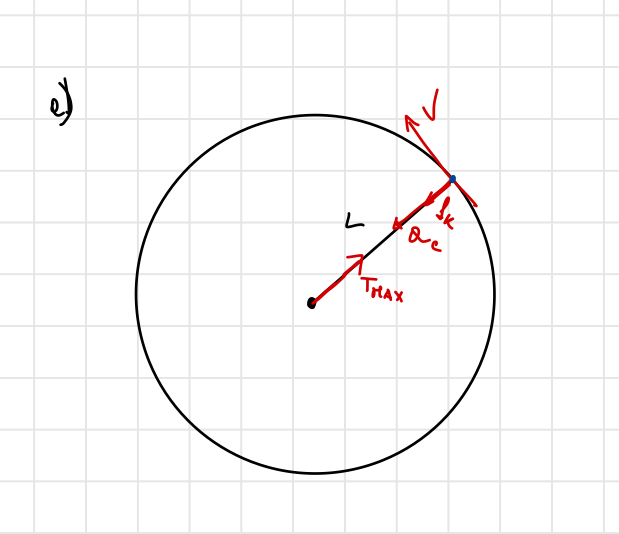
Ho provato partendo dalla II Legge di Newton
$T_max = m*v^2/L + u_k*F_n $
Non riesco a capire come calcolare la velocità. Credo dal fatto che sapendo che percorre 7 metri prima di fermarsi possa ricavare una seconda equazione. Ho provato con semplici leggi orarie ma non mi torna. Qualche idea? Grazie mille
Un punto materiale è vincolato a muoversi in un piano orizzontale con attrito. Il coefficiente di attrito dinamico u è pari a 0.1. Il punto materiale è collegato ad un filo di lunghezza L=7m e ruota rispetto ad un punto fisso O. Il filo è in grado di sostenere una tensione massima pari a Tmax=10 N. Si immagini di aumentare progressivamente la velocità di rotazione del punto materiale. Ad un certo istante il filo si spezza ed il punto materiale percorre una distanza pari a d=7 m (Calcolata rispetto al punto di rilascio) prima di fermarsi.
Quanto vale la massa del punto materiale?
Ho schematizzato banalmente in questo modo:
Ho provato partendo dalla II Legge di Newton
$T_max = m*v^2/L + u_k*F_n $
Non riesco a capire come calcolare la velocità. Credo dal fatto che sapendo che percorre 7 metri prima di fermarsi possa ricavare una seconda equazione. Ho provato con semplici leggi orarie ma non mi torna. Qualche idea? Grazie mille
Risposte
"Batixono":
Ho provato partendo dalla II Legge di Newton
$T_max = m*v^2/L + u_k*F_n $
Non riesco a capire come calcolare la velocità. e
La tensione del filo non dipende dall'attrito, quindi è $T_max = m*v^2/L $, da cui ricavi una relazione velocità/massa, e in sostanza l'energia cinetica. Poi questa si azzera con i 7m di strisciamento, quindi...
Ma dopo i 7 metri l'energia cinetica si è convertita interamente in energia termica dovuta all'attrito?
"Batixono":
Ma dopo i 7 metri l'energia cinetica si è convertita interamente in energia termica dovuta all'attrito?
Se no, dove sarebbe finita?
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo