Momento di inerzia di una superficie cilindrica
non riesco a capire bene come si ricava il momento di inerzia di una superficie cilindrica che ruota attorno ad un asse perpendicolare all'asse del cilindro:
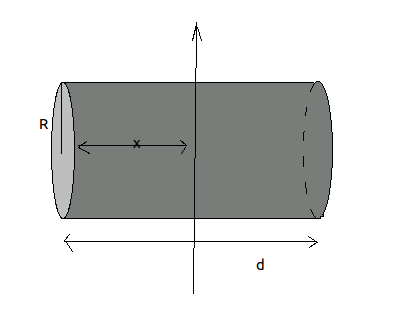
nel mio libro c'è scritto che il cilindro può essere scomposto in tanti anelli infinitesimi con momento di inerzia $dI = 1/2 dmR^2 + dmx^2$ quindi $I$ si ottiene moltiplicando per 2 e integrando da $0$ a $d/2$; non mi è chiaro però come mai scrive quella formula per l'anello (perchè c'è $1/2$ ?) e perchè è necessario moltiplicare per 2 e integrare fra quegli estremi... nel caso di una bacchetta con asse passante per in centro lo stesso libro integrava tra $-d/2$ e $d/2$ senza moltiplicare nulla, si potrebbe fare lo stesso qui o sarebbe un errore?

nel mio libro c'è scritto che il cilindro può essere scomposto in tanti anelli infinitesimi con momento di inerzia $dI = 1/2 dmR^2 + dmx^2$ quindi $I$ si ottiene moltiplicando per 2 e integrando da $0$ a $d/2$; non mi è chiaro però come mai scrive quella formula per l'anello (perchè c'è $1/2$ ?) e perchè è necessario moltiplicare per 2 e integrare fra quegli estremi... nel caso di una bacchetta con asse passante per in centro lo stesso libro integrava tra $-d/2$ e $d/2$ senza moltiplicare nulla, si potrebbe fare lo stesso qui o sarebbe un errore?
Risposte
Tu intendi calcolare il momento di inerzia di un "guscio cilindrico" sottile, rispetto ad un asse perpendicolare all'asse del cilindro nel punto medio della lunghezza, è così?
Allora, andiamo con ordine.
Considera prima un riferimento piano cartesiano $Oxy$, sul tuo foglio, e disegna una circonferenza di raggio $R$ con centro in $O$ . Supponi che su questa circonferenza sia uniformemente distribuita una massa $M$ , cioè il rapporto $M/R = cost$ . Questo è evidentemente una "distribuzione piana" di massa.
C'è un terzo asse che devi considerare, l'asse $z$ perpendicolare al foglio e passante per il centro $O$ della circonferenza.
Il momento d' inerzia rispetto ad un qualunque diametro è sempre lo stesso, quindi : $I_x = I_y$
Il momento di inerzia rispetto all'asse $z$ è uguale semplicemente a : $I_z = M*R^2$ , poichè tutta la massa è a distanza $R$ da $z$ ( bisognerebbe dimostrarlo , con un semplicissimo integrale, ma suppongo tu lo sappia già) .
Risulta anche che $I_z = I_O$ , cioè è uguale al momento d iinerzia polare rispetto al polo $O$ .
ORa si ha, nel caso in esame : $ I_z = I_x + I_y = 2*I_x = M*R^2$ ( anche qui, suppongo che ti sia chiaro il motivo, se no devo mettermi a spiegare un sacco di roba di Geometria delle masse)
Perciò, si deduce che : $I_x = 1/2M*R^2$ ----(1)
Questo è appunto il momento di inerzia di un anello di massa $M$ rispetto ad un qualsiasi asse diametrale : tutta la massa è concentrata nell'anello, e basta moltiplicarla per $R^2$
Adesso , per quanto riguarda il guscio cilindrico, il tuo libro dice : facciamo a "fettine" di ampiezza $dx$ il guscio . Ogni fettina è un anello ( come prima) di massa $dm$ , avente il momento di inerzia proprio $1/2*dm*R^2$ , al quale va sommato il termine di trasporto $dm*x^2$ .
PEr calcolare il momento d inerzia totale rispetto all'asse detto , si può fare in entrambi i modi : o moltiplichi per 2 e quindi integri da $0$ a $d/2$ . Oppure , NON moltiplichi per 2 , e allora integri da $-d/2$ a $+d/2$
Allora, andiamo con ordine.
Considera prima un riferimento piano cartesiano $Oxy$, sul tuo foglio, e disegna una circonferenza di raggio $R$ con centro in $O$ . Supponi che su questa circonferenza sia uniformemente distribuita una massa $M$ , cioè il rapporto $M/R = cost$ . Questo è evidentemente una "distribuzione piana" di massa.
C'è un terzo asse che devi considerare, l'asse $z$ perpendicolare al foglio e passante per il centro $O$ della circonferenza.
Il momento d' inerzia rispetto ad un qualunque diametro è sempre lo stesso, quindi : $I_x = I_y$
Il momento di inerzia rispetto all'asse $z$ è uguale semplicemente a : $I_z = M*R^2$ , poichè tutta la massa è a distanza $R$ da $z$ ( bisognerebbe dimostrarlo , con un semplicissimo integrale, ma suppongo tu lo sappia già) .
Risulta anche che $I_z = I_O$ , cioè è uguale al momento d iinerzia polare rispetto al polo $O$ .
ORa si ha, nel caso in esame : $ I_z = I_x + I_y = 2*I_x = M*R^2$ ( anche qui, suppongo che ti sia chiaro il motivo, se no devo mettermi a spiegare un sacco di roba di Geometria delle masse)
Perciò, si deduce che : $I_x = 1/2M*R^2$ ----(1)
Questo è appunto il momento di inerzia di un anello di massa $M$ rispetto ad un qualsiasi asse diametrale : tutta la massa è concentrata nell'anello, e basta moltiplicarla per $R^2$
Adesso , per quanto riguarda il guscio cilindrico, il tuo libro dice : facciamo a "fettine" di ampiezza $dx$ il guscio . Ogni fettina è un anello ( come prima) di massa $dm$ , avente il momento di inerzia proprio $1/2*dm*R^2$ , al quale va sommato il termine di trasporto $dm*x^2$ .
PEr calcolare il momento d inerzia totale rispetto all'asse detto , si può fare in entrambi i modi : o moltiplichi per 2 e quindi integri da $0$ a $d/2$ . Oppure , NON moltiplichi per 2 , e allora integri da $-d/2$ a $+d/2$
grazie mille, mi hai chiarito tutti i dubbi


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo