Momenti di forze e argano

[snower]

Ragazzi mi sono imbattuto in questo problema abbastanza complicato, che ho provato a risolvere e ad ottenere un risultato, ma penso sia completamente sbagliato... Purtroppo non ho le soluzioni in quanto si tratta di un esercizio pari dal Tiplet -.-

Un'automobile di $10^3kg$ viene scaricata da una nave per mezzo di un argano. L'asse del ruotino dell'argano si rompe e l'automobile, inizialmente in quiete, cade. Durante la caduta dell'automobile, non si produce strisciamento tra la fune, la carrucola e il tamburo dell'argano. Il momento d'inerzia del tamburo è $320kgm^2$ e quello della carrucola $4kgm^2$ Il raggio del tamburo dell'argano è $0.80m$, quello della carrucola $0.30m$. Si trovi la velocità dell'automobile all'istante in cui raggiunge l'acqua supponendo che essa all'istante 0 si trovi a $5m$ sul livello dell'acqua.

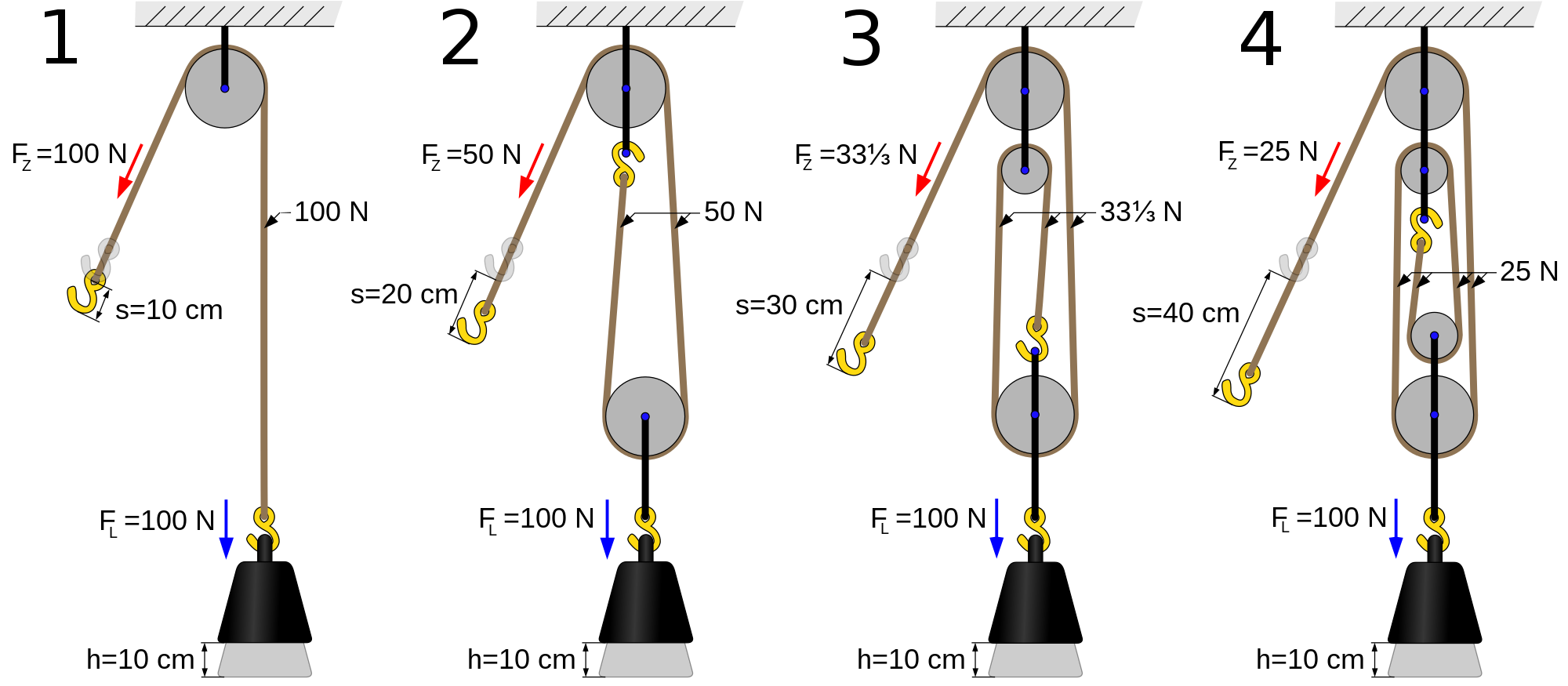
Diciamo che il disegno è fatto così, come nella prima immaginetta di sinistra. Solo che al posto del gancio giallo di sinistra c'è il tamburo dell'argano, quindi un altro elemento rotante a cui è legato il filo, e ovviamente al posto di quel peso c'è l'automobile. Inoltre la carrucola non è legata da un altro filo dall'alto ma ha un sostegno solido dal basso. Ovviamente lasciate perdere i dati della figura qua, non c'entrano nulla

Io ho provato a risolverlo così, ma molto probabilmente sono davvero fuori strada... Ho impostato un sistema a 3 equazioni in 3 incognite. Supponendo il berso posiitivo dell'asse verticale quello discendente:

$ { ( mg-T1=ma ),( T1r1-T2r2=I1alpha ),( T2r2=I2alpha ):} $

I numeri 1 e 2 sono pedici! T1 indica la tensione che agisce sull'auto verso l'alto e quella verso il basso sulla parte destra della carrucola. T2 è la tensione sulla sinistra della carrucola e che agisce sull'argano.
Primo dubbio: non è che sono uguali?
In questo sistema io ho tre incognite: le due tensioni e $alpha$. Ora secondo dubbio: ho supposto che tale accelerazione sia uguale da entrambe le parti. Ho sbagliato giusto?
Intanto così facendo e risolvendo il sistema col metodo di Gauss, mi trovo subito, senza passare per il valore delle due tensioni. cjhe $alpha=7.17 (rad)/s^2$, che quindi $a=2.15 m/s^2$ e che quindi l'auto tocca l'acqua con $v=16.7 (km)/h$
Io penso di aver sbagliato tutto, proprio l'impostazione del problema... Qualcuno di voi può darmi una mano?

[professorkappa]

Non ho guardato il sistema, ma a me viene circa 28.7 km/h.
Principio dei lavori virtuali, non ti serve impostare il problema.

Cmounque lo guardo dopo per vedere l'errore.

[professorkappa]

"asido":Ragazzi mi sono imbattuto in questo problema abbastanza complicato, che ho provato a risolvere e ad ottenere un risultato, ma penso sia completamente sbagliato... Purtroppo non ho le soluzioni in quanto si tratta di un esercizio pari dal Tiplet -.-

Un'automobile di $10^3kg$ viene scaricata da una nave per mezzo di un argano. L'asse del ruotino dell'argano si rompe e l'automobile, inizialmente in quiete, cade. Durante la caduta dell'automobile, non si produce strisciamento tra la fune, la carrucola e il tamburo dell'argano. Il momento d'inerzia del tamburo è $320kgm^2$ e quello della carrucola $4kgm^2$ Il raggio del tamburo dell'argano è $0.80m$, quello della carrucola $0.30m$. Si trovi la velocità dell'automobile all'istante in cui raggiunge l'acqua supponendo che essa all'istante 0 si trovi a $5m$ sul livello dell'acqua.

Diciamo che il disegno è fatto così, come nella prima immaginetta di sinistra. Solo che al posto del gancio giallo di sinistra c'è il tamburo dell'argano, quindi un altro elemento rotante a cui è legato il filo, e ovviamente al posto di quel peso c'è l'automobile. Inoltre la carrucola non è legata da un altro filo dall'alto ma ha un sostegno solido dal basso. Ovviamente lasciate perdere i dati della figura qua, non c'entrano nulla

Io ho provato a risolverlo così, ma molto probabilmente sono davvero fuori strada... Ho impostato un sistema a 3 equazioni in 3 incognite. Supponendo il berso posiitivo dell'asse verticale quello discendente:

$ { ( mg-T1=ma ),( T1r1-T2r2=I1alpha ),( T2r2=I2alpha ):} $

I numeri 1 e 2 sono pedici! T1 indica la tensione che agisce sull'auto verso l'alto e quella verso il basso sulla parte destra della carrucola. T2 è la tensione sulla sinistra della carrucola e che agisce sull'argano.
Primo dubbio: non è che sono uguali?
In questo sistema io ho tre incognite: le due tensioni e $alpha$. Ora secondo dubbio: ho supposto che tale accelerazione sia uguale da entrambe le parti. Ho sbagliato giusto?
Intanto così facendo e risolvendo il sistema col metodo di Gauss, mi trovo subito, senza passare per il valore delle due tensioni. cjhe $alpha=7.17 (rad)/s^2$, che quindi $a=2.15 m/s^2$ e che quindi l'auto tocca l'acqua con $v=16.7 (km)/h$
Io penso di aver sbagliato tutto, proprio l'impostazione del problema... Qualcuno di voi può darmi una mano?

Ribadendo i fatto che se non sono richieste le tensioni delle funi, il principio dei lavori virtuali e' la via migliore per risolvere il problema, gli errori son 2:

Innanzitutto, le incognite sono 5:
Tensione $T_1$ e $T_2$. 2 (2 incognite)
$\alpha_1$ accelerazione del tamburo e $\alpha_2$, accelerazione della carrucola (in generale non uguali, e sicuramente non uguali in questo caso).
$a$ L'accelerazione della macchina.

3 equazioni le hai scritte. le altre 2 vengono dai vincoli cinematici (per esempio $a=r_2\alpha_2$)