Gru omogenea imperniata in P
Una gru omogenea $(PQ)$ di massa $2500 kg$ e lunghezza $7.5m$ sostiene un carico di $15000N$. L'estremo inferiore della gru è imperniata in $P$ e l'altro estremo è tirato da un cavo $C$. Determinare la tensione del cavo e la forza esercitata dal perno se la gru è in equilibrio con l'angolo $theta=30°$
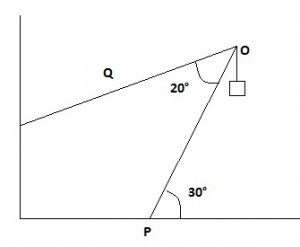
Allora sicuramente si devono applicare le due equazioni cardinali della statica, ma come impostare la prima, non ci riesco proprio: ho provato così, ma sono sicruo che è un disastro:
$m+M+T+R_p=0$
proiettata sugli assi x, orizzontale, parallela e concorde con PO e Y verticale verso l'alto si ha:
$R_(px)-Tcos20°$
$R_(py)-m-Mg+Tsen20°$
sicuramente sono sbagliate, specie per via di questi angoli non riesco proprio a vederne le componenti

Allora sicuramente si devono applicare le due equazioni cardinali della statica, ma come impostare la prima, non ci riesco proprio: ho provato così, ma sono sicruo che è un disastro:
$m+M+T+R_p=0$
proiettata sugli assi x, orizzontale, parallela e concorde con PO e Y verticale verso l'alto si ha:
$R_(px)-Tcos20°$
$R_(py)-m-Mg+Tsen20°$
sicuramente sono sbagliate, specie per via di questi angoli non riesco proprio a vederne le componenti
Risposte
Direi che qualcosa non va...nella prima equazione che hai scritto (come anche nell'ultima) come fa a comparire m+M (che è una massa) sommato a T e Rp che sono forze? Non vedi che non torna dimensionalmente?
Quello che devi fare è applicare $\sum F=0$ su ciascuno di quei corpi singolarmente.
Quello che devi fare è applicare $\sum F=0$ su ciascuno di quei corpi singolarmente.
E' un esercizio simile ai precedenti.
Se definisci l'equazione dei momenti utilizzando il perno come asse hai tutti gli elementi per calcolare la tensione della fune: hai la massa (e quindi il peso) della gru da applicare nel suo CDM (dato che è omogenea), hai già il peso del carico e sai dove applicarlo (e l'angolo da utilizzare è lo stesso del peso della gru), hai il punto di applicazione della tensione della fune e pure l'angolo da utilizzare; l'unica incognita rimane la tensione. Calcoli e poi vai avanti per trovare le componenti della reazione del perno ...
Se definisci l'equazione dei momenti utilizzando il perno come asse hai tutti gli elementi per calcolare la tensione della fune: hai la massa (e quindi il peso) della gru da applicare nel suo CDM (dato che è omogenea), hai già il peso del carico e sai dove applicarlo (e l'angolo da utilizzare è lo stesso del peso della gru), hai il punto di applicazione della tensione della fune e pure l'angolo da utilizzare; l'unica incognita rimane la tensione. Calcoli e poi vai avanti per trovare le componenti della reazione del perno ...
Allora applicando la II equaz. card. statica $M=0$
Momento peso gru:
$mg (L/2) sen60°$, sicuramente corretto però $mg (L/2)$ ok poi sto $sen30$ è usato stesso nella regola del momento d'inerzia?
Importante: Perchè $F_c L sen60°$ positivo e $T L sen20°$ negativo, non riesco a capire come scegli i versi? Senza figura non riesco proprio
------------------
I Equ. cardinale statica:
1-Proiezione su asse x: perchè peso della gru non ha componenti lungo l'asse x,eppure la gru è inclinata quindi dovrebbe averne
2-Anche qui i versi non mi sono chiari ne sull'asse x che su y, mi spiego:
Asse x:
$Tcos10°$ tira a sinistra e R_x tira a sinistra, perchè hanno verso disuguale?
Asse y:
$mg$(perchè non c'è un $sen30°$ vicino?) è diretta verso il basso, $F_c$ anche, $Tsen10°$ verso il basso e $R_y$ verso il basso, perchè quest'ultimo cambia segno?
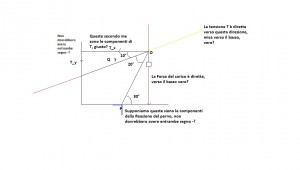
Spero riesca a farmelo capire, altrimenti veramente non ho speranza
Scusa se faccio le figure, ma credo che siano il modo più semplice per farmi capire
Momento peso gru:
$mg (L/2) sen60°$, sicuramente corretto però $mg (L/2)$ ok poi sto $sen30$ è usato stesso nella regola del momento d'inerzia?
Importante: Perchè $F_c L sen60°$ positivo e $T L sen20°$ negativo, non riesco a capire come scegli i versi? Senza figura non riesco proprio
------------------
I Equ. cardinale statica:
1-Proiezione su asse x: perchè peso della gru non ha componenti lungo l'asse x,eppure la gru è inclinata quindi dovrebbe averne
2-Anche qui i versi non mi sono chiari ne sull'asse x che su y, mi spiego:
Asse x:
$Tcos10°$ tira a sinistra e R_x tira a sinistra, perchè hanno verso disuguale?
Asse y:
$mg$(perchè non c'è un $sen30°$ vicino?) è diretta verso il basso, $F_c$ anche, $Tsen10°$ verso il basso e $R_y$ verso il basso, perchè quest'ultimo cambia segno?

Spero riesca a farmelo capire, altrimenti veramente non ho speranza
Scusa se faccio le figure, ma credo che siano il modo più semplice per farmi capire
Troppe domande, spero di farcela ... 
Eq.momenti: non ho capito qual è il tuo dubbio (inerzia?), anche perché dici che è corretto ... quindi ?!?
I versi li puoi scegliere come vuoi (la convenzione di solito vuole positivo il senso antiorario e negativo quello orario; qui ho fatto il contraio, ma va bene lo stesso.). Comunque puoi anche ipotizzare che abbiano lo stesso verso, alla fine uno ti risultera negativo che significa che va al contrario di quello che avevi ipotizzato.
1)Se scegli un sistema di riferimento in cui l'asse $x$ è orizzontale (parallelo al piano terrestre) allora quando scomponi la forza peso (che è perpendicolare al piano) la componente orizzontale è nulla. Non confondere le componenti del peso della gru (oriz. e vert.) con il momento generatro dal peso della gru (che infatti c'è e la fa ruotare)
2)
Asse $x$: che la reazione del perno tiri a sinistra è una tua supposizione; calcolala e poi si vede dove va ...
Asse $y$: non c'è un $sin(alpha)$ perché la componente verticale del peso è uguale al peso; al solito, il verso della reazione del perno è una tua supposizione ...
(prosegue in un altro post)

Eq.momenti: non ho capito qual è il tuo dubbio (inerzia?), anche perché dici che è corretto ... quindi ?!?
I versi li puoi scegliere come vuoi (la convenzione di solito vuole positivo il senso antiorario e negativo quello orario; qui ho fatto il contraio, ma va bene lo stesso.). Comunque puoi anche ipotizzare che abbiano lo stesso verso, alla fine uno ti risultera negativo che significa che va al contrario di quello che avevi ipotizzato.
1)Se scegli un sistema di riferimento in cui l'asse $x$ è orizzontale (parallelo al piano terrestre) allora quando scomponi la forza peso (che è perpendicolare al piano) la componente orizzontale è nulla. Non confondere le componenti del peso della gru (oriz. e vert.) con il momento generatro dal peso della gru (che infatti c'è e la fa ruotare)
2)
Asse $x$: che la reazione del perno tiri a sinistra è una tua supposizione; calcolala e poi si vede dove va ...
Asse $y$: non c'è un $sin(alpha)$ perché la componente verticale del peso è uguale al peso; al solito, il verso della reazione del perno è una tua supposizione ...
(prosegue in un altro post)
Disegno:
Per quanto riguarda la direzione della tensione: hai mai visto una fune che "spinge"? Le funi, per definizione "tirano", quindi la direzione delle componenti della tensione saranno (molto probabilmente) verso il basso e verso sinistra.
Per quanto riguarda i versi(segni): come detto, puoi fissarli come vuoi (anche quelli della tensione se vuoi), basta che tu sia sempre COERENTE e se ti viene un valore negativo significa che "va" al contrario di come lo avevi fissato.
Secondo me, un po' di confusione nasce dal fatto che le equazioni spesso vengono scritte in due modi diversi e mi spiego.
Se la gru sta ferma significa che la risultante delle forze orizzontali, di quelle verticali e dei momenti deve essere nulla. Spesso però, per fare prima, si eguagliano le forze (o i momenti) che "pensiamo" vadano in un verso con quelli che "pensiamo" vadano nell'altro, ed è qui che nasce, spesso, la confusione.
Per quanto riguarda la direzione della tensione: hai mai visto una fune che "spinge"? Le funi, per definizione "tirano", quindi la direzione delle componenti della tensione saranno (molto probabilmente) verso il basso e verso sinistra.
Per quanto riguarda i versi(segni): come detto, puoi fissarli come vuoi (anche quelli della tensione se vuoi), basta che tu sia sempre COERENTE e se ti viene un valore negativo significa che "va" al contrario di come lo avevi fissato.
Secondo me, un po' di confusione nasce dal fatto che le equazioni spesso vengono scritte in due modi diversi e mi spiego.
Se la gru sta ferma significa che la risultante delle forze orizzontali, di quelle verticali e dei momenti deve essere nulla. Spesso però, per fare prima, si eguagliano le forze (o i momenti) che "pensiamo" vadano in un verso con quelli che "pensiamo" vadano nell'altro, ed è qui che nasce, spesso, la confusione.
axpgn allora mi devi scusare, non ci sto a capì più niente:
1: Te come fai a pensare che $mg(L/2)sen60°$ e $F_cLsen60°$ spingano in senso orario? Sono d'accordo che la tensione tiri, quindi giustamente andrà comunque contraria alle altre due forze, però la tua deduzione deigli altri due momenti è solo una tua deduzione, sei te che la pensi così, dammi una spiegazione che posso usarla in ogni esercizio, altrimenti vado ancora di più nel pallone.
2:Nelle proiezioni rispetto ad x e y delle forze, te mi dici: è una tua(cioè mia) pensata circa che $R_y$ e $R_x$ spingano a sinistra esotto, andrebbe calcolata, allora mi spieghi come dovrebbe fare uno che se la deve ancora calcolare a stabilire sto maledetto segno?
3:Perchè te metti nella proiezione con y:$mg+F_c+Tsen10°$ stabilisci segno più (perchè spingono in basso o tirano a sinistra), mentre $R_y$ chi te l'ha detto che spinga in alto a sto punto?
Cioè alla fine dei conti, te stabilisci che il segno + va per forze che non so vanno a destra, - al contrario e fin qua OK, però come fai ad essere sicuro che i segni che usi per la rezione del perno siano corretti, se te stesso mi dici, che prima va calcolata per conoscere dove va?
1: Te come fai a pensare che $mg(L/2)sen60°$ e $F_cLsen60°$ spingano in senso orario? Sono d'accordo che la tensione tiri, quindi giustamente andrà comunque contraria alle altre due forze, però la tua deduzione deigli altri due momenti è solo una tua deduzione, sei te che la pensi così, dammi una spiegazione che posso usarla in ogni esercizio, altrimenti vado ancora di più nel pallone.
2:Nelle proiezioni rispetto ad x e y delle forze, te mi dici: è una tua(cioè mia) pensata circa che $R_y$ e $R_x$ spingano a sinistra esotto, andrebbe calcolata, allora mi spieghi come dovrebbe fare uno che se la deve ancora calcolare a stabilire sto maledetto segno?
3:Perchè te metti nella proiezione con y:$mg+F_c+Tsen10°$ stabilisci segno più (perchè spingono in basso o tirano a sinistra), mentre $R_y$ chi te l'ha detto che spinga in alto a sto punto?
Cioè alla fine dei conti, te stabilisci che il segno + va per forze che non so vanno a destra, - al contrario e fin qua OK, però come fai ad essere sicuro che i segni che usi per la rezione del perno siano corretti, se te stesso mi dici, che prima va calcolata per conoscere dove va?
Allora ... comincio col ripetere un concetto detto prima diverse volte (attenzione, non è una osservazione nei tuoi confronti, ma è solo per ribadire un concetto base che non mi pare chiaro).
Prima di tutto si fissa un sistema di riferimento: un origine e due assi perpendicolari.
Dopodiché individuate le grandezze in gioco (forze, lunghezze , velocità, ecc. ), per quelle vettoriali si fissa una direzione (se possibile) ed un verso; alcune direzioni sono note (anzi obbligate) come quelle della forza peso o delle tensioni, altre no. Idem per i versi con una importante variante: i versi incogniti li possiamo fissare come ci pare (o come ci pare più sensato) ma con l'avvertenza che se il segno della grandezza che infine troviamo è DISCORDE col sistema di riferimento, il verso della grandezza andrà invertito. Per esempio, fissato il solito piano cartesiano con i positivi verso destra e verso l'alto, se ipotizzo che una forza "tiri" a sinistra, dovrò aspettarmi un valore negativo per il suo modulo; se invece sarà positivo, significa che in realtà tira verso destra. E chiaro questo modo di procedere? (poi vado avanti con i punti ...)
Prima di tutto si fissa un sistema di riferimento: un origine e due assi perpendicolari.
Dopodiché individuate le grandezze in gioco (forze, lunghezze , velocità, ecc. ), per quelle vettoriali si fissa una direzione (se possibile) ed un verso; alcune direzioni sono note (anzi obbligate) come quelle della forza peso o delle tensioni, altre no. Idem per i versi con una importante variante: i versi incogniti li possiamo fissare come ci pare (o come ci pare più sensato) ma con l'avvertenza che se il segno della grandezza che infine troviamo è DISCORDE col sistema di riferimento, il verso della grandezza andrà invertito. Per esempio, fissato il solito piano cartesiano con i positivi verso destra e verso l'alto, se ipotizzo che una forza "tiri" a sinistra, dovrò aspettarmi un valore negativo per il suo modulo; se invece sarà positivo, significa che in realtà tira verso destra. E chiaro questo modo di procedere? (poi vado avanti con i punti ...)
ok supponiamo:
forza "tira" a sinistra, se però esce modulo positivo, devo ricambiare segno nell'operazione, o lascio invariato?
forza "tira" a sinistra, se però esce modulo positivo, devo ricambiare segno nell'operazione, o lascio invariato?
Data la premessa nel post precedente passiamo ai vari punti:
1)Sì, è una mia supposizione che quei momenti tirino in senso orario, ma è coerente con quanto detto.
Quando parliamo di momenti tutto dipende dal punto scelto come polo o asse; nel nostro caso, avendo scelto il perno P, è "sensato" pensare che il peso della gru ed il carico abbiano un momento in senso orario, ma che questo sia vero ne potremo avere la conferma solo dopo averli calcolati. Supposto di aver scelto il senso orario come positivo, se questi momenti saranno positivi (e quindi concordi col sistema di riferimento) allora il senso è corretto altrimenti se sarranno negativi il verso sarà il contrario.
2)Vedi la premessa; stabilisci un verso e verifica alla fine se è concorde o meno con quello che avevi fissato.
3)Stesso concetto di prima ed aggiungo che l'equazione ti dice che la risultante delle forze verticali deve essere nulla; io per comodità sono saltato direttamente ad eguagliare le forze che vanno in "su" con quelle che vanno in "giù" e questo, come detto anche precedentemente, può generare confusione; quindi parti pure dall'equazione fondamentale $F_r=0$.
Spero di averti chiarito le idee, se no ... ci riproviamo ...
1)Sì, è una mia supposizione che quei momenti tirino in senso orario, ma è coerente con quanto detto.
Quando parliamo di momenti tutto dipende dal punto scelto come polo o asse; nel nostro caso, avendo scelto il perno P, è "sensato" pensare che il peso della gru ed il carico abbiano un momento in senso orario, ma che questo sia vero ne potremo avere la conferma solo dopo averli calcolati. Supposto di aver scelto il senso orario come positivo, se questi momenti saranno positivi (e quindi concordi col sistema di riferimento) allora il senso è corretto altrimenti se sarranno negativi il verso sarà il contrario.
2)Vedi la premessa; stabilisci un verso e verifica alla fine se è concorde o meno con quello che avevi fissato.
3)Stesso concetto di prima ed aggiungo che l'equazione ti dice che la risultante delle forze verticali deve essere nulla; io per comodità sono saltato direttamente ad eguagliare le forze che vanno in "su" con quelle che vanno in "giù" e questo, come detto anche precedentemente, può generare confusione; quindi parti pure dall'equazione fondamentale $F_r=0$.
Spero di averti chiarito le idee, se no ... ci riproviamo ...

"75america":
ok supponiamo:
forza "tira" a sinistra, se però esce modulo positivo, devo ricambiare segno nell'operazione, o lascio invariato?
No, DEVI sempre essere COERENTE in tutto lo svolgimento. Se esce DISCORDE significa che tira al contrario di come avevi pensato, ma il valore che hai trovato è GIUSTO (o meglio è coerente con il sistema e le direzioni ed i versi da te stabiliti).
Se cambiassi il segno del valore trovato dovresti cambiare anche il verso nel disegno da te fatto e rivedere tutte le formule ed espressioni da te calcolate.
Quindi userai i valori che hai trovato ed eventualmente alla fine potrai dire nella soluzione che "... la forza tal dei tali in realtà tira verso destra col valore ....".
Ok?
Ciao, Alex
ok Alex,mi spiegheresti perchè nel calcolo del Momento Peso Gru:
$mg (L/2) sen60$ scusa ma l'angolo di 60 l'angolo compreso tra il punto di applicazione della forza peso(che non so dove sia) e l'asta omogenea,cioè perchè 60 e no 30?
$mg (L/2) sen60$ scusa ma l'angolo di 60 l'angolo compreso tra il punto di applicazione della forza peso(che non so dove sia) e l'asta omogenea,cioè perchè 60 e no 30?
Prendiamo un punto e una forza qualsiasi; allora si chiama momento della forza il prodotto vettoriale della vettore forza per il vettore distanza tra il polo (asse) e il punto di applicazione della forza; questo prodotto corrisponde a $Fdsin(theta)$ dove $F$ è il modulo della forza applicata, $d$ è il modulo del vettore distanza (in pratica la distanza tra il polo e il punto di applicazione della forza) e $theta$ è l'angolo tra le direzioni del vettore forza e del vettore distanza.
Nel caso specifico (il momento generato dal peso della gru) la forza è il peso della gru $mg$, la distanza (che hai anche scritto) è $L/2$ perché possiamo considerare il peso come se fosse concentrato tutto nel suo Centro di Massa (CdM) ed essendo l'asta omogenea e simmetrica, il suo CdM si trova a metà lunghezza; infine l'angolo $theta$ è pari a $60°$ perché questo è l'angolo formato dalla direzione del peso (verticale) con la direzione della distanza (dal perno al CdM), infatti è il complementare di $30°$ che la gru forma con l'orizzontale (osserva il triangolo rettangolo che si forma tra piano, gru e direzione del peso).
Ok?
Nel caso specifico (il momento generato dal peso della gru) la forza è il peso della gru $mg$, la distanza (che hai anche scritto) è $L/2$ perché possiamo considerare il peso come se fosse concentrato tutto nel suo Centro di Massa (CdM) ed essendo l'asta omogenea e simmetrica, il suo CdM si trova a metà lunghezza; infine l'angolo $theta$ è pari a $60°$ perché questo è l'angolo formato dalla direzione del peso (verticale) con la direzione della distanza (dal perno al CdM), infatti è il complementare di $30°$ che la gru forma con l'orizzontale (osserva il triangolo rettangolo che si forma tra piano, gru e direzione del peso).
Ok?
ok direzione del peso


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo