[EX] Uovo à la Fourier
Così come l'uovo a occhio di bue, o à la coque, esiste anche l'uovo à la Fourier... Solo che non si mangia, ma si risolve. 
(Ero indeciso se metterlo in Fisica o in Analisi... Poi ho scelto la prima, perché voglio essere davvero "globale" e movimentare un po' anche le altre stanze. )
)
***
Esercizio:
Si supponga che un uovo \(\mathcal{U}\) coincida con una palla di \(\mathbb{R}^3\) di raggio \(r>0\), la cui temperatura iniziale è uniforme ed uguale a \(u_0\).
Immergendo l'uovo in una grossa quantità d'acqua a temperatura costante \(U>u_0\), dopo quanto tempo la temperatura al centro dell'uovo raggiunge la temperatura d'equilibrio \(U\)?
(Ero indeciso se metterlo in Fisica o in Analisi... Poi ho scelto la prima, perché voglio essere davvero "globale" e movimentare un po' anche le altre stanze.
***
Esercizio:
Si supponga che un uovo \(\mathcal{U}\) coincida con una palla di \(\mathbb{R}^3\) di raggio \(r>0\), la cui temperatura iniziale è uniforme ed uguale a \(u_0\).
Immergendo l'uovo in una grossa quantità d'acqua a temperatura costante \(U>u_0\), dopo quanto tempo la temperatura al centro dell'uovo raggiunge la temperatura d'equilibrio \(U\)?
Risposte
Se l'uovo non è un uovo ma una sfera di raggio $R$, è opportuno, penso, scrivere le equazioni di Fourier della trasmissione del calore in coordinate sferiche, e visto che il problema è a simmetria sferica la distribuzione delle temperature varia solo col raggio $r$ e col tempo $t$. .
Si dovrebbero considerare dei gusci sferici di spessore $dr$ , nei quali tra la superficie esterna e quella interna c'è un differenza di temperatura $dT$....
Ma detto questo,io mi fermo.
Si dovrebbero considerare dei gusci sferici di spessore $dr$ , nei quali tra la superficie esterna e quella interna c'è un differenza di temperatura $dT$....
Ma detto questo,io mi fermo.
Non conosco bene l'argomento, e mi permetto solo di esprimere la mia idea. Dato che il problema è così posto, penso proprio che la difficoltà stia nel non approssimare l'uovo ad una sfera, e a calcolare il flusso attraverso un corpo generato dalla rotazione di una figura simile a questa
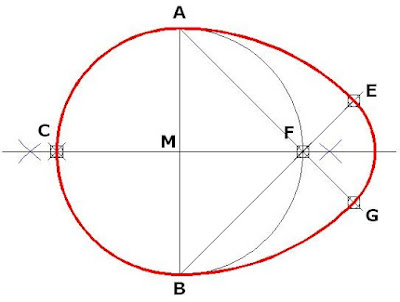
P.S. il mio cervello aveva del tutto saltato la parte in cui si diceva che poteva essere considerato una sfera, scusate xD

P.S. il mio cervello aveva del tutto saltato la parte in cui si diceva che poteva essere considerato una sfera, scusate xD
"A naso" credo che la temperatura al centro tenda alla temperatura di equilibrio per tempi tendenti all'infinito. Quindi la risposta è mai.
Ho provato a svolgere e posto solo fino al punto a cui sono arrivato, sperando di riuscire a capire se va bene e come procedere successivamente e quindi terminare.
Partendo con le osservazioni fatte anche da navigatore, mi risulta una equazione differenziale così fatta:
$1/r^2partial/(partialr)(r^2(partialu)/(partialr))-k(partialu)/(partialt)=0$
Con condizioni al bordo omogeneizzate
$u_r(0,t)=0$
$u_r(r_e,t)+cu(r_e,t)=0$
e condizione iniziale
$u(r,0)=u_0'$
Separando le variabili in $u(r,t)=R(r)T(t)$ mi risulta
$T=T_0e^(-m/kt)$
con $m>0$e
$R''+2/rR'+mR=0$
con le condizioni che sono (dovendo essere $Tne0$)
$R'(0)=0$
$R'(r_e)+cR(r_e)=0$
Partendo con le osservazioni fatte anche da navigatore, mi risulta una equazione differenziale così fatta:
$1/r^2partial/(partialr)(r^2(partialu)/(partialr))-k(partialu)/(partialt)=0$
Con condizioni al bordo omogeneizzate
$u_r(0,t)=0$
$u_r(r_e,t)+cu(r_e,t)=0$
e condizione iniziale
$u(r,0)=u_0'$
Separando le variabili in $u(r,t)=R(r)T(t)$ mi risulta
$T=T_0e^(-m/kt)$
con $m>0$e
$R''+2/rR'+mR=0$
con le condizioni che sono (dovendo essere $Tne0$)
$R'(0)=0$
$R'(r_e)+cR(r_e)=0$
Ciao Gugo, c'è qualche risposta che ti soddisfa?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo