Esercizio di Meccanica sulla variazione di energia meccanica.
Salve a tutti,
sono alle prese con il seguente esercizio:
"Un carrellino giocattolo di massa $0,80kg$ percorre un piano inclinato di $30°$ come mostra la figura. La sua velocità iniziale in cima alla pendenza vale $1,1 m/s$. La superficie inclinata sulla quale scende esercita una forza di attrito di $5,0N$ sul carrellino.
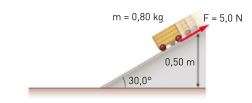
Quanto vale la sua energia meccanica iniziale? Il carrellino raggiunge la base della discesa?$
Tenendo presente che
$$L_{F_{att}}=\Delta E,$$
si ha
$$mgh_2-mgh_1-\frac{1}{2}mv_1^2= F\left(\frac{h_1-h_2}{sin(30°)}\right),$$
dove con $h_1$ e $h_2$ ho indicato rispettivamente l'altezza da cui parte e quella a cui si ferma.
Risolvendo tale equazione ho ottenuto il valore di $h_2$ che conferma il risultato, ovvero che il blocco non raggiunge la base del piano inclinato.
Mi chiedevo se sarebbe bastato verificare quanto segue: supponendo che il blocco arrivi alla base del piano inclinato il lavoro della forza d'attrito sarebbe $$L_{F_{att}}=\frac{h_1}{\sin(30°)} F=-5J;$$ al contrario la variazione di energia meccanica sarebbe $$-E_i=\frac{1}{2}mv_1^2+mgh_1=-4,4J,$$
poiché raggiunto il suolo l'energia meccanica finale sarebbe $0$; da questo si deduce che il blocco deve fermarsi prima di giungere alla base del piano inclinato.
Grazie mille a chi vorrà rispondere!
sono alle prese con il seguente esercizio:
"Un carrellino giocattolo di massa $0,80kg$ percorre un piano inclinato di $30°$ come mostra la figura. La sua velocità iniziale in cima alla pendenza vale $1,1 m/s$. La superficie inclinata sulla quale scende esercita una forza di attrito di $5,0N$ sul carrellino.

Quanto vale la sua energia meccanica iniziale? Il carrellino raggiunge la base della discesa?$
Tenendo presente che
$$L_{F_{att}}=\Delta E,$$
si ha
$$mgh_2-mgh_1-\frac{1}{2}mv_1^2= F\left(\frac{h_1-h_2}{sin(30°)}\right),$$
dove con $h_1$ e $h_2$ ho indicato rispettivamente l'altezza da cui parte e quella a cui si ferma.
Risolvendo tale equazione ho ottenuto il valore di $h_2$ che conferma il risultato, ovvero che il blocco non raggiunge la base del piano inclinato.
Mi chiedevo se sarebbe bastato verificare quanto segue: supponendo che il blocco arrivi alla base del piano inclinato il lavoro della forza d'attrito sarebbe $$L_{F_{att}}=\frac{h_1}{\sin(30°)} F=-5J;$$ al contrario la variazione di energia meccanica sarebbe $$-E_i=\frac{1}{2}mv_1^2+mgh_1=-4,4J,$$
poiché raggiunto il suolo l'energia meccanica finale sarebbe $0$; da questo si deduce che il blocco deve fermarsi prima di giungere alla base del piano inclinato.
Grazie mille a chi vorrà rispondere!
Risposte
Sostanzialmente va bene, ma la forma lascia un po' a desiderare.
Per esempio: tu dici che se il carrello raggiunge la base del piano
Poi dici anche
Una via alternativa, forse più semplice, sarebbe stata quella di trovare l'accelerazione del carrello (negativa) e trovare lo spazio percorso prima di fermarsi. Ma va bene anche il tuo modo.
Per esempio: tu dici che se il carrello raggiunge la base del piano
il lavoro della forza d'attrito sarebbe $$L_{F_{att}}=\frac{h_1}{\sin(30°)} F=-5J;$$ al contrario la variazione di energia meccanica sarebbe $$-E_i=\frac{1}{2}mv_1^2+mgh_1=-4,4J,$$Com'è che sommando l'energia cinetica e potenziale viene un valore negativo? D'accordo, ci siamo capiti: ma è scritto male.
Poi dici anche
poiché raggiunto il suolo l'energia meccanica finale sarebbe $0$E perchè? Sarà zero l'energia potenziale, ma quella cinetica?
Una via alternativa, forse più semplice, sarebbe stata quella di trovare l'accelerazione del carrello (negativa) e trovare lo spazio percorso prima di fermarsi. Ma va bene anche il tuo modo.
Si disordinatisimo, per questo si e' perso l'energia cinetica finale.
Ed e' solo l'attrito che fa lavoro negativo, il resto è positivo
Hai tutti i dati, ti calcoli la velocità finale, e vedi che il segno meno serviva
$ (Ec +Ep)f -(Ec +EP) i =-Wfa $
Ed e' solo l'attrito che fa lavoro negativo, il resto è positivo
Hai tutti i dati, ti calcoli la velocità finale, e vedi che il segno meno serviva
$ (Ec +Ep)f -(Ec +EP) i =-Wfa $
Scusate, ma evidentemente ho interpretato male il problema perché ho posto volutamente l'energia cinetica finale uguale a zero pensando che si fermasse. Quindi quando mi chiede se raggiunge la discesa non non va interpretato come "si ferma alla base del piano"?
Per capire se si ferma devi calcolati la velocità finale con quell' attrito.
Allora ho interpretato male il testo, perché ho pensato che si fermasse alla base oppure ad una quota diversa da quella nulla. Grazie mille!
Scusate se torno a scrivere, ma ho cercato di calcolare l'altezza cui giunge il carrellino in maniera puramente teorica. Sono partito dunque da
$$\frac{1}{2}mv_2^2+mgh_2-\frac{1}{2}mv_1^2-mgh_1=L_{F_{att}}.$$
Ho calcolato innanzitutto la velocità finale: la forza totale agente sul corpo è
$$F_{tot}=-mg\sin(30°)+F_{att},$$
e quindi $$a=F_{tot}/m$$.
Dopodiché ho scritto $$v_2^2=2\frac{F_{tot}}{m}\left(\frac{h_1-h_2}{sin(30°)}\right)+v_1^2.$$
Il lavoro della forza di attrito è $$\mathcal{L}=-F_{att}\left(\frac{h_1-h_2}{sin(30°)}\right).$$
Uguagliando ottengo
$$\frac{1}{2}m\left(2\frac{F_{tot}}{m}\left(\frac{h_1-h_2}{sin(30°)}\right)+v_1^2\right)+mgh_2-\frac{1}{2}mv_1^2-mgh_1=-F_{att}\left(\frac{h_1-h_2}{sin(30°)}\right).$$
Se sviluppo però viene fuori che $$h_2=\frac{\left(\frac{F_{tot}-F_{att}}{sin(30°)}+mg\right)}{\left(\frac{F_{att}-F_{tot}}{sin(30°)}+mg\right)}h_1,$$
che significherebbe $h_2=0$. Evidentemente c'è qualcosa che non va ma non sto capendo cosa. Potreste soccorrermi di nuovo?
Grazie infinitamente!
$$\frac{1}{2}mv_2^2+mgh_2-\frac{1}{2}mv_1^2-mgh_1=L_{F_{att}}.$$
Ho calcolato innanzitutto la velocità finale: la forza totale agente sul corpo è
$$F_{tot}=-mg\sin(30°)+F_{att},$$
e quindi $$a=F_{tot}/m$$.
Dopodiché ho scritto $$v_2^2=2\frac{F_{tot}}{m}\left(\frac{h_1-h_2}{sin(30°)}\right)+v_1^2.$$
Il lavoro della forza di attrito è $$\mathcal{L}=-F_{att}\left(\frac{h_1-h_2}{sin(30°)}\right).$$
Uguagliando ottengo
$$\frac{1}{2}m\left(2\frac{F_{tot}}{m}\left(\frac{h_1-h_2}{sin(30°)}\right)+v_1^2\right)+mgh_2-\frac{1}{2}mv_1^2-mgh_1=-F_{att}\left(\frac{h_1-h_2}{sin(30°)}\right).$$
Se sviluppo però viene fuori che $$h_2=\frac{\left(\frac{F_{tot}-F_{att}}{sin(30°)}+mg\right)}{\left(\frac{F_{att}-F_{tot}}{sin(30°)}+mg\right)}h_1,$$
che significherebbe $h_2=0$. Evidentemente c'è qualcosa che non va ma non sto capendo cosa. Potreste soccorrermi di nuovo?
Grazie infinitamente!
Vuoi trovare dove si ferma il carrello? Scrivi l'energia cinetica iniziale $1/2mv_0^2$, aggiungi il lavoro dovuto alla variazione di energia potenziale: $mg(h_0 - h_f)$: questo è la colonna dell'attivo del bilancio energetico. Il passivo è il lavoro della forza di attrito: $F_a*(h_0 - h_f)/(sin 30)$; uguagli attivo e passivo e ti viene fuori una equazione con $h_(fin)$ come incognita. Se $h_f <= 0$ il carrello arriva in fondo (ovvero, si ferma sottoterra), se no, no.
Non mi pare il caso di sollevare tutto questo polverone...
Non mi pare il caso di sollevare tutto questo polverone...
Ma sbaglio o mi avevi corretto proprio tu dicendo che avrei dovuto aggiungere l'energia cinetica finale?
"jakojako":
Ma sbaglio o mi avevi corretto proprio tu dicendo che avrei dovuto aggiungere l'energia cinetica finale?
Ti avevo fatto notare che non è detto che al suolo il carrello sia fermo. Dipende da che cosa intendi con finale: può significare: al suolo, oppure: quando il carrello si ferma.
I conti da fare cambiano nei due casi. Quello che ti messo per ultimo considera finale quando si ferma (e allora ovviamente l'energia cinetica finale è 0), per cui, per rispondere alla domanda, si deve guardare si si ferma sopra o sotto il suolo; nell'altro caso, si tratta di vedere se, al suolo, le velocità è zero o maggiore di zero.
Ok, va benissimo. Se scorri su, la prima cosa che avevo scritto corrispondeva al contenuto della tua risposta. Ma ero stato ripreso, per cui avevo cercato altre strade.
Eri stato "ripreso", per usare la tua espressione, per due questioni più di forma che di sostanza. Ti avevo anche detto che il tuo metodo andava bene.
Grazie mille e scusa il fraintendimento allora!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo