Esercizietto su dipolo elettrico
Mi trovo "sconfitto" da questo primo esercizio sui dipoli
Dimostrare che, posto un dipolo elettrico in un campo elettrico uniforme $E_0$, parallelo
e concorde al momento elettrico del dipolo, esiste nel campo risultante una superficie
equipotenziale sferica, con centro nel centro del dipolo. Calcolare il campo elettrico nei
punti di tale superficie.
in entrambe le richieste.
La mia idea era stata di mettere il potenziale in funzione del coseno dell'angolo centrando il sistema coordinato nella metà dell'asse ideale che congiunge le due cariche de dipolo e per simmetria considerarne solo il piano xy complanare al foglio.
$V(\theta)=pr/(4pi\epsilon_0r^3)cos\theta+rkcos\theta$
Il $kcos\theta$ l'ho ottenuto considerando che il campo E0=k=costante, quindi integrando nelle tre variabili x,y,z il potenziale che ne risulta sarà kx. E riscrivendo x in funzione di coorinate polari avrei: $k(rcos\theta)$
Sommando quindi i due contributi al potenziale totale avrei:
$V_(TOT)=(pr+(4pir^2\epsilon_0)K)/(4pi\epsilon_0r^3)cos\theta$ (1)
il vantaggio è che ora avrei un potenziale dipendente dalla sola theta, quindi derivadolo posso trovare il campo elettrico, la mia idea è che sapendo che il modulo di $E_(TOT)=E_0+E_D$ con $E_D$ quello del dipolo,potrei sostituendo mettere tutto in relazione di un E e mostrare che avrò $r^3=G*E_0$ e mostrare che ho in effetti una sfera centrata nell'origine a metà del dipolo.
Ho quindi derivato la (1) rispetto a theta:
equazione valida scalarmente (non sono vettori)
$E_(TOT)=(pr+(4pi\epsilon_0r^2)K)/(4pi\epsilon_0r^3)sin\theta=>r^3=(pr+(4pi\epsilon_0r^2)K)/(4pi\epsilon_0(E_0+E_D))sin\theta$
Ma insomma non sto a continuare perché da qui in poi sono calcoli e non viene
Volevo solo scrivere l'impostazione di cui in realtà nutro forti dubbi e ci sono un paio di punti che credo siano sbaglaiti
Vi ringrazio per l'aiuto già ora
Dimostrare che, posto un dipolo elettrico in un campo elettrico uniforme $E_0$, parallelo
e concorde al momento elettrico del dipolo, esiste nel campo risultante una superficie
equipotenziale sferica, con centro nel centro del dipolo. Calcolare il campo elettrico nei
punti di tale superficie.
in entrambe le richieste.
La mia idea era stata di mettere il potenziale in funzione del coseno dell'angolo centrando il sistema coordinato nella metà dell'asse ideale che congiunge le due cariche de dipolo e per simmetria considerarne solo il piano xy complanare al foglio.
$V(\theta)=pr/(4pi\epsilon_0r^3)cos\theta+rkcos\theta$
Il $kcos\theta$ l'ho ottenuto considerando che il campo E0=k=costante, quindi integrando nelle tre variabili x,y,z il potenziale che ne risulta sarà kx. E riscrivendo x in funzione di coorinate polari avrei: $k(rcos\theta)$
Sommando quindi i due contributi al potenziale totale avrei:
$V_(TOT)=(pr+(4pir^2\epsilon_0)K)/(4pi\epsilon_0r^3)cos\theta$ (1)
il vantaggio è che ora avrei un potenziale dipendente dalla sola theta, quindi derivadolo posso trovare il campo elettrico, la mia idea è che sapendo che il modulo di $E_(TOT)=E_0+E_D$ con $E_D$ quello del dipolo,potrei sostituendo mettere tutto in relazione di un E e mostrare che avrò $r^3=G*E_0$ e mostrare che ho in effetti una sfera centrata nell'origine a metà del dipolo.
Ho quindi derivato la (1) rispetto a theta:
equazione valida scalarmente (non sono vettori)
$E_(TOT)=(pr+(4pi\epsilon_0r^2)K)/(4pi\epsilon_0r^3)sin\theta=>r^3=(pr+(4pi\epsilon_0r^2)K)/(4pi\epsilon_0(E_0+E_D))sin\theta$
Ma insomma non sto a continuare perché da qui in poi sono calcoli e non viene
Volevo solo scrivere l'impostazione di cui in realtà nutro forti dubbi e ci sono un paio di punti che credo siano sbaglaiti
Vi ringrazio per l'aiuto già ora
Risposte
Mi sembra un po' strano che esista questa superficie.
La soluzione ce l'hai ?
La soluzione ce l'hai ?
Sì in effetti non le ho copiate:
$R^3=p/(4pi\epsilon_0E_0), E(P)=3E_0cos\theta$
PS: anche a me parrebbe non esistere vista così, al massimo se $\vecp$ fosse discorde. Mah.
$R^3=p/(4pi\epsilon_0E_0), E(P)=3E_0cos\theta$
PS: anche a me parrebbe non esistere vista così, al massimo se $\vecp$ fosse discorde. Mah.
Il calcolo deriva da:
$(p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 0$
da cui
$r^3 = p/(4 \pi \epsilon \ E_0)$.
Ora, intanto all'inizio mi ero fatto ingannare da quel "concorde" che c'e' scritto nel testo dell'esercizio.
In realta' il campo $E_0$ e' discorde, ovvero e' orientato nel verso opposto al momento di dipolo.
L'equazione che ho scritto sopra deriva dal fatto che se si prende il piano ortogonale al momento, e si pone il potenziale di questo piano a zero, allora bisogna che dall'equazione possa sparire il termine coseno, ovvero che il potenziale dipenda solo dal raggio.
Se il campo $E_0$ fosse stato concorde, da un lato del piano a potenziale zero si avrebbero solo potenziali positivi, e dall'altro solo potenziali negativi, quindi non esisterebbe la superficie sferica cercata.
$(p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 0$
da cui
$r^3 = p/(4 \pi \epsilon \ E_0)$.
Ora, intanto all'inizio mi ero fatto ingannare da quel "concorde" che c'e' scritto nel testo dell'esercizio.
In realta' il campo $E_0$ e' discorde, ovvero e' orientato nel verso opposto al momento di dipolo.
L'equazione che ho scritto sopra deriva dal fatto che se si prende il piano ortogonale al momento, e si pone il potenziale di questo piano a zero, allora bisogna che dall'equazione possa sparire il termine coseno, ovvero che il potenziale dipenda solo dal raggio.
Se il campo $E_0$ fosse stato concorde, da un lato del piano a potenziale zero si avrebbero solo potenziali positivi, e dall'altro solo potenziali negativi, quindi non esisterebbe la superficie sferica cercata.
"dargo":
PS: anche a me parrebbe non esistere vista così, al massimo se $\vecp$ fosse discorde. Mah.
Si, infatti e' discorde, non concorde.
Credo di doverti fare alcune domande perché non ho capito alcune condizioni.
Mi pare che anche tu abbia preso la situazione con sistema di riferimento che indicavo ecc.. e fin qui ok, i problemi giungono sull'equazione:
$(p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 0$
Analizziamola
1)
$(p\ \cos \theta)/(4 \pi \epsilon \ r^2)$
potenziale del dipolo, ok
$ - E_0\ r\ cos \theta$
dovresti sottrarre il potenziale del piano, perfetto, ma... perchè l'espressione indicata rappresenterebbe un potenziale? Dimensionalmente ci siamo, ma non capisco come tu l'abbia effettivamente ricavata
Le coordinate polari suggeriscono $rcos\theta$ così da scrivere in formule a un certo r e un certo theta il potenziale del piano. Ma perché lo moltiplichiamo per il campo? E perché moltiplicando per il campo le coordinate polari trovo un potenziale? Non mi è chiaro
2)
Altro punto dubbio è il perché la imponi =0. Ho compreso che vogliamo toglierci dai piedi quel coseno, ma perché fisicamente la differenza dei due potenziali la consideri proprio zero?
In realtà ci saranno altre sfere che avranno differenza differente -perdona l'allitterazione sgradevole-, tipo una costante $c$ e prendiamolaadesempio c=5, quindi avrei potuto considerare:
$(p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 5$
e chi mi garantisce che se la trovo per =0 esista una equipotenziale anche per =5?
Spero avrai voglia di spiegarmi e di non tediarti con i miei dubbi
Grazie per il tuo aiuto (indispensabile) datomi.
Mi pare che anche tu abbia preso la situazione con sistema di riferimento che indicavo ecc.. e fin qui ok, i problemi giungono sull'equazione:
$(p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 0$
Analizziamola
1)
$(p\ \cos \theta)/(4 \pi \epsilon \ r^2)$
potenziale del dipolo, ok
$ - E_0\ r\ cos \theta$
dovresti sottrarre il potenziale del piano, perfetto, ma... perchè l'espressione indicata rappresenterebbe un potenziale? Dimensionalmente ci siamo, ma non capisco come tu l'abbia effettivamente ricavata
Le coordinate polari suggeriscono $rcos\theta$ così da scrivere in formule a un certo r e un certo theta il potenziale del piano. Ma perché lo moltiplichiamo per il campo? E perché moltiplicando per il campo le coordinate polari trovo un potenziale? Non mi è chiaro
2)
Altro punto dubbio è il perché la imponi =0. Ho compreso che vogliamo toglierci dai piedi quel coseno, ma perché fisicamente la differenza dei due potenziali la consideri proprio zero?
In realtà ci saranno altre sfere che avranno differenza differente -perdona l'allitterazione sgradevole-, tipo una costante $c$ e prendiamolaadesempio c=5, quindi avrei potuto considerare:
$(p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 5$
e chi mi garantisce che se la trovo per =0 esista una equipotenziale anche per =5?
Spero avrai voglia di spiegarmi e di non tediarti con i miei dubbi
Grazie per il tuo aiuto (indispensabile) datomi.
Allora, definiamo meglio lo scenario.
Abbiamo il momento di dipolo nell'origine $(0,0,0)$ ed e' il vettore $(0,0,p)$.
Poi abbiamo il campo elettrico in questo modo: $(0,0,-E_0)$.
Poniamo il piano $xy$ a potenziale zero.
L'esercizio ci dice che esiste questa sfera a potenziale costante che e' centrata nell'origine.
Ne segue che la sfera viene tagliata dal piano $xy$.
Quindi una parte della sfera e' a potenziale zero, e siccome la sfera e' equipotenziale, allora tutta la sfera e' a potenziale zero.
Da qui impostiamo l'equazione:
$ (p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 0 $
che e' la somma dei due potenziali.
Forse adesso risulta piu' chiaro il discorso.
Mancava la parte in cui viene spiegato che la sfera taglia il piano $xy$.
Abbiamo il momento di dipolo nell'origine $(0,0,0)$ ed e' il vettore $(0,0,p)$.
Poi abbiamo il campo elettrico in questo modo: $(0,0,-E_0)$.
Poniamo il piano $xy$ a potenziale zero.
L'esercizio ci dice che esiste questa sfera a potenziale costante che e' centrata nell'origine.
Ne segue che la sfera viene tagliata dal piano $xy$.
Quindi una parte della sfera e' a potenziale zero, e siccome la sfera e' equipotenziale, allora tutta la sfera e' a potenziale zero.
Da qui impostiamo l'equazione:
$ (p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 0 $
che e' la somma dei due potenziali.
Forse adesso risulta piu' chiaro il discorso.
Mancava la parte in cui viene spiegato che la sfera taglia il piano $xy$.
"dargo":
Le coordinate polari suggeriscono $rcos\theta$ così da scrivere in formule a un certo r e un certo theta il potenziale del piano. Ma perché lo moltiplichiamo per il campo? E perché moltiplicando per il campo le coordinate polari trovo un potenziale? Non mi è chiaro
Beh dire $r\ cos \theta$ e' come dire $z$.
Un campo uniforme $(0,0,E_0)$ ha come potenziale $(0,0,E_0\z)$.
Ok ora la situazione mi è chiara, non avevo ben capito il fatto per piano.
Devo dire però che non sono convinto al 100% di averne dimostrato l'esistenza,ti spiego perché:
* L'esistenza della sfera equipotenziale implica che esista questo piano xy, e noi abbiamo verificato che tale piano esiste.
* Tuttavia non è vero che se esiste il piano (cosa che abbiamo dimostrato) esiste la sfera. In sostanza non mi pare che piano=>sfera. E' anche vero che nell'equazione troviamo un raggio al cubo (sintomo di sfera) ma, non capisco perché vi sia questa implicazione diretta tra esistenza del piano e sfera. La vedo solo in senso contrario.
L'esercizio non assicura nelle ipotesi l'esistenza della sfera,quindi non è azzardato dire
?
Devo dire però che non sono convinto al 100% di averne dimostrato l'esistenza,ti spiego perché:
* L'esistenza della sfera equipotenziale implica che esista questo piano xy, e noi abbiamo verificato che tale piano esiste.
* Tuttavia non è vero che se esiste il piano (cosa che abbiamo dimostrato) esiste la sfera. In sostanza non mi pare che piano=>sfera. E' anche vero che nell'equazione troviamo un raggio al cubo (sintomo di sfera) ma, non capisco perché vi sia questa implicazione diretta tra esistenza del piano e sfera. La vedo solo in senso contrario.
L'esercizio non assicura nelle ipotesi l'esistenza della sfera,quindi non è azzardato dire
L'esercizio ci dice che esiste questa sfera a potenziale costante che e' centrata nell'origine.
Ne segue che la sfera viene tagliata dal piano xy.
?
Aspetta.
Vediamo di ricostruire bene la catena di deduzioni, che vengono fatte spesso in modo automatico, a mente, ma non sono affatto ovvie.
L'esercizio ci dice che esiste una sfera, centrata nell'origine, a potenziale costante.
Noi dobbiamo determinare il potenziale e possibilmente determinare il raggio e dimostrare che tale sfera esiste.
Un'altra deduzione e' che se riesco a determinare il potenziale di un punto della sfera, allora so il potenziale di tutta la sfera.
Se ad esempio esiste un piano che attraversa l'origine ed e' a potenziale costante allora so gia' il potenziale della sfera, perche' il piano taglia la sfera.
Va bene anche un cono con il vertice nell'origine, che sia a potenziale costante.
Attenzione, non e' NECESSARIO che tale piano o cono esista. Ma se esiste, e' un grosso aiuto per arrivare alla soluzione.
Ora, guardiamo questa immagine, che e' il potenziale creato da un dipolo.
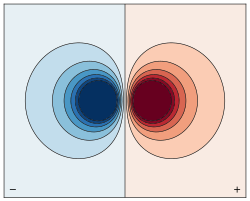
E' il piano xz, (sarebbe uguale anche a yz), cioe' una sezione dello spazio tridimensionale. Le linee sono a potenziale costante.
E' subito evidente che c'e' quella linea retta a meta', che indica un piano a potenziale costante.
Forse e' quel grosso aiuto che cerchiamo.
Domanda per te: siccome prima ho detto che andrebbe bene anche un cono a potenziale costante, cosa dovrebbe apparire nell'immagine come indizio che e' presente uno di questi coni ?
Un dubbio che potrebbe sorgere, che forse e' il tuo dubbio, e' perche' non va bene una generica superficie a potenziale costante, invece che un piano o un cono.
La risposta e' che il piano o il cono si estendono dal centro all'infinito, e quindi la sfera che cerchiamo deve incrociare il piano/cono. Quelle altre superfici equipotenziali che si vedono nell'immagine che assomigliamo a dei palloni sono limitate.
Ora siccome noi non conosciamo il raggio della sfera, tale raggio potrebbe anche essere molto grande e quindi la sfera potrebbe non incrociare tale superficie.
Ora dobbiamo aggiungere il potenziale del campo uniforme $E_0$.
Qui la questione si risolve abbastanza velocemente, siccome il potenziale del campo uniforme e' fatto da tanti piani equipotenziali, Questi piani sono paralleli al piano $xy$ e ognuno ha potenziale $E_0z$.
Il potenziale finale e' la somma dei due. Fissiamo il potenziale zero sul piano $xy$ stesso sia per il potenziale del dipolo, che per quello del campo fisso. Non e' importante, ma rende tutto meno complicato.
Dovrebbe essere abbastanza facile intuire che il piano $xy$ rimane a potenziale costante.
Ok, ora ho l'indizio importante che cercavo.
Ho un piano a potenziale costante, la sfera deve incrociare questo piano, quindi conosco il potenziale della sfera, che ho stabilito a zero.
Adesso cosa faccio: vado a scrivere la formula del potenziale finale (la somma di quello del dipolo e del campo uniforme) e la pongo uguale a zero.
Ovvero tramite questa formula trovero' in modo generico un insieme di punti, e il passo successivo sara' di stabilire se l'insieme di punti e' una sfera.
$ (p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 0 $
e' sempre la stessa.
Le soluzioni di quell'equazione sono:
$\theta = \pi/2$
e
$r^3 = p/(4 \pi \epsilon \ E_0) $.
Domanda per te:
cos'e' $\theta = \pi/2$ ?
che superficie e' ?
L'altra $r^3 = p/(4 \pi \epsilon \ E_0) $ e' un insieme di punti a distanza costante dall'origine, ovvero una sfera.
Bene, direi che siamo arrivati in fondo. Abbiamo visto che la sfera esiste, ed abbiamo il raggio e il potenziale.
Domanda: e' l'unica sfera a potenziale costante, magari esistono altre sfere a potenziale diverso da zero ?
Beh, e' l'unica, perche' anche se esistesse un'altra sfera con raggio diverso, la sfera (centrata nell'origine), comunque deve tagliare il piano $xy$, che sappiamo essere a potenziale costante e uguale a zero. Ma dall'equazione risulta che esiste solo una sfera a potenziale zero. Quindi la soluzione e' unica.
No, no, no....
l'esistenza del piano equipotenziale NON implica l'esistenza di alcuna sfera e viceversa, ovvero l'esistenza della sfera NON implica alcun piano equipotenziale.
Il piano esiste perche' ho esaminato i potenziali di dipolo e del campo uniforme. Ed e' "abbastanza" facile da vedere.
La sfera si SUPPONE solamente che esiste. (Il testo dell'esercizio la da per certa, ma noi facciamo un passo indietro e la supponiamo solamente).
MA, se sono certo che un piano equipotenziale taglia la sfera equipotenziale, allora il potenziale della sfera e del piano devono essere uguali.
Quindi se conosco il potenziale del piano, conosco anche quello della sfera. Hurra !
Ok, ma e' una dimostrazione per assurdo.
Ovvero, io ipotizzo l'esistenza di questa sfera.
Da quel momento ragiono come se la sfera esistesse davvero.
Se pero' ad un certo punto cado in contraddizione, allora tutto il mio castello di carte cade, e l'ipotesi che la sfera esiste cade.
Ad esempio:
IPOTESI:
Esiste una sfera blah blah blah......
TESI (o svolgimento):
Blah blah blah.... e quindi il raggio della sfera e' $r = \sqrt(10+cos\theta)$.
Contraddizione -> il raggio non e' costante, quindi la sfera non e' una sfera, quindi la sfera non esiste.
Vediamo di ricostruire bene la catena di deduzioni, che vengono fatte spesso in modo automatico, a mente, ma non sono affatto ovvie.
L'esercizio ci dice che esiste una sfera, centrata nell'origine, a potenziale costante.
Noi dobbiamo determinare il potenziale e possibilmente determinare il raggio e dimostrare che tale sfera esiste.
Un'altra deduzione e' che se riesco a determinare il potenziale di un punto della sfera, allora so il potenziale di tutta la sfera.
Se ad esempio esiste un piano che attraversa l'origine ed e' a potenziale costante allora so gia' il potenziale della sfera, perche' il piano taglia la sfera.
Va bene anche un cono con il vertice nell'origine, che sia a potenziale costante.
Attenzione, non e' NECESSARIO che tale piano o cono esista. Ma se esiste, e' un grosso aiuto per arrivare alla soluzione.
Ora, guardiamo questa immagine, che e' il potenziale creato da un dipolo.

E' il piano xz, (sarebbe uguale anche a yz), cioe' una sezione dello spazio tridimensionale. Le linee sono a potenziale costante.
E' subito evidente che c'e' quella linea retta a meta', che indica un piano a potenziale costante.
Forse e' quel grosso aiuto che cerchiamo.
Domanda per te: siccome prima ho detto che andrebbe bene anche un cono a potenziale costante, cosa dovrebbe apparire nell'immagine come indizio che e' presente uno di questi coni ?
Un dubbio che potrebbe sorgere, che forse e' il tuo dubbio, e' perche' non va bene una generica superficie a potenziale costante, invece che un piano o un cono.
La risposta e' che il piano o il cono si estendono dal centro all'infinito, e quindi la sfera che cerchiamo deve incrociare il piano/cono. Quelle altre superfici equipotenziali che si vedono nell'immagine che assomigliamo a dei palloni sono limitate.
Ora siccome noi non conosciamo il raggio della sfera, tale raggio potrebbe anche essere molto grande e quindi la sfera potrebbe non incrociare tale superficie.
Ora dobbiamo aggiungere il potenziale del campo uniforme $E_0$.
Qui la questione si risolve abbastanza velocemente, siccome il potenziale del campo uniforme e' fatto da tanti piani equipotenziali, Questi piani sono paralleli al piano $xy$ e ognuno ha potenziale $E_0z$.
Il potenziale finale e' la somma dei due. Fissiamo il potenziale zero sul piano $xy$ stesso sia per il potenziale del dipolo, che per quello del campo fisso. Non e' importante, ma rende tutto meno complicato.
Dovrebbe essere abbastanza facile intuire che il piano $xy$ rimane a potenziale costante.
Ok, ora ho l'indizio importante che cercavo.
Ho un piano a potenziale costante, la sfera deve incrociare questo piano, quindi conosco il potenziale della sfera, che ho stabilito a zero.
Adesso cosa faccio: vado a scrivere la formula del potenziale finale (la somma di quello del dipolo e del campo uniforme) e la pongo uguale a zero.
Ovvero tramite questa formula trovero' in modo generico un insieme di punti, e il passo successivo sara' di stabilire se l'insieme di punti e' una sfera.
$ (p\ \cos \theta)/(4 \pi \epsilon \ r^2) - E_0\ r\ cos \theta = 0 $
e' sempre la stessa.
Le soluzioni di quell'equazione sono:
$\theta = \pi/2$
e
$r^3 = p/(4 \pi \epsilon \ E_0) $.
Domanda per te:
cos'e' $\theta = \pi/2$ ?
che superficie e' ?
L'altra $r^3 = p/(4 \pi \epsilon \ E_0) $ e' un insieme di punti a distanza costante dall'origine, ovvero una sfera.
Bene, direi che siamo arrivati in fondo. Abbiamo visto che la sfera esiste, ed abbiamo il raggio e il potenziale.
Domanda: e' l'unica sfera a potenziale costante, magari esistono altre sfere a potenziale diverso da zero ?
Beh, e' l'unica, perche' anche se esistesse un'altra sfera con raggio diverso, la sfera (centrata nell'origine), comunque deve tagliare il piano $xy$, che sappiamo essere a potenziale costante e uguale a zero. Ma dall'equazione risulta che esiste solo una sfera a potenziale zero. Quindi la soluzione e' unica.
* L'esistenza della sfera equipotenziale implica che esista questo piano xy, e noi abbiamo verificato che tale piano esiste.
* Tuttavia non è vero che se esiste il piano (cosa che abbiamo dimostrato) esiste la sfera. In sostanza non mi pare che piano=>sfera. E' anche vero che nell'equazione troviamo un raggio al cubo (sintomo di sfera) ma, non capisco perché vi sia questa implicazione diretta tra esistenza del piano e sfera. La vedo solo in senso contrario.
No, no, no....
l'esistenza del piano equipotenziale NON implica l'esistenza di alcuna sfera e viceversa, ovvero l'esistenza della sfera NON implica alcun piano equipotenziale.
Il piano esiste perche' ho esaminato i potenziali di dipolo e del campo uniforme. Ed e' "abbastanza" facile da vedere.
La sfera si SUPPONE solamente che esiste. (Il testo dell'esercizio la da per certa, ma noi facciamo un passo indietro e la supponiamo solamente).
MA, se sono certo che un piano equipotenziale taglia la sfera equipotenziale, allora il potenziale della sfera e del piano devono essere uguali.
Quindi se conosco il potenziale del piano, conosco anche quello della sfera. Hurra !
L'esercizio non assicura nelle ipotesi l'esistenza della sfera,quindi non è azzardato dire
Ok, ma e' una dimostrazione per assurdo.
Ovvero, io ipotizzo l'esistenza di questa sfera.
Da quel momento ragiono come se la sfera esistesse davvero.
Se pero' ad un certo punto cado in contraddizione, allora tutto il mio castello di carte cade, e l'ipotesi che la sfera esiste cade.
Ad esempio:
IPOTESI:
Esiste una sfera blah blah blah......
TESI (o svolgimento):
Blah blah blah.... e quindi il raggio della sfera e' $r = \sqrt(10+cos\theta)$.
Contraddizione -> il raggio non e' costante, quindi la sfera non e' una sfera, quindi la sfera non esiste.
Innanzituto grazie per la copiosa risposta. DIrei che ha chiarito tutti i punti dubbi e ora potrei azzardare soluzioni di problemi simili avendola capita.
Nutro inoltre una "sana invidia" (so che può sembrare ossimorico ma esiste) per queste capacità analitiche, davvero una risposta perfetta
Provo timidamente a rispondere ai tuoi validi imput:
1)
Direi due rette che si intersecano (sezione di un cono con un piano?
1bis)
Potrebbe estendere la ricerca anche un paraboloide ellittico (e chi più ne ha più ne metta), basta che sia infinita? Giusto?
2)
Fatico a decifrarla, nel senso che se fosse $x=pi/2$ direi un piano di valore sulle ascisse di pi/2, ma ho un theta non un x. In coordinate sferiche mi parrebbe un piano di angolo theta al variare di rho qualunque. non saprei..
Non avrei mai immaginato che da un esercizio del genere avrei ottenuto così tatni stimoli. Ne sono piacevolmente colpito
Grazie ancora.
Nutro inoltre una "sana invidia" (so che può sembrare ossimorico ma esiste) per queste capacità analitiche, davvero una risposta perfetta
Provo timidamente a rispondere ai tuoi validi imput:
1)
"siccome prima ho detto che andrebbe bene anche un cono a potenziale costante, cosa dovrebbe apparire nell'immagine come indizio che e' presente uno di questi coni ?"
Direi due rette che si intersecano (sezione di un cono con un piano?
1bis)
La risposta e' che il piano o il cono si estendono dal centro all'infinito, e quindi la sfera che cerchiamo deve incrociare il piano/cono. Quelle altre superfici equipotenziali che si vedono nell'immagine che assomigliamo a dei palloni sono limitate
Potrebbe estendere la ricerca anche un paraboloide ellittico (e chi più ne ha più ne metta), basta che sia infinita? Giusto?
2)
Domanda per te: cos'e' θ=π/2 ? che superficie e' ?
Fatico a decifrarla, nel senso che se fosse $x=pi/2$ direi un piano di valore sulle ascisse di pi/2, ma ho un theta non un x. In coordinate sferiche mi parrebbe un piano di angolo theta al variare di rho qualunque. non saprei..
Non avrei mai immaginato che da un esercizio del genere avrei ottenuto così tatni stimoli. Ne sono piacevolmente colpito
Grazie ancora.
"dargo":
Innanzituto grazie per la copiosa risposta. DIrei che ha chiarito tutti i punti dubbi e ora potrei azzardare soluzioni di problemi simili avendola capita.
Nutro inoltre una "sana invidia" (so che può sembrare ossimorico ma esiste) per queste capacità analitiche, davvero una risposta perfetta
Ti ringrazio per il complimento.
Piu' che altro si tratta di cocciutaggine a voler tirare fuori una soluzione a tutti i costi.
Come disse il buon Einstein:
Non preoccuparti delle difficoltà che incontri in matematica, ti posso assicurare che le mie sono ancora più grosse.
Provo timidamente a rispondere ai tuoi validi imput:
1) [quote]"siccome prima ho detto che andrebbe bene anche un cono a potenziale costante, cosa dovrebbe apparire nell'immagine come indizio che e' presente uno di questi coni ?"
Direi due rette che si intersecano (sezione di un cono con un piano?
[/quote]
Ok, bene.
1bis) [quote]La risposta e' che il piano o il cono si estendono dal centro all'infinito, e quindi la sfera che cerchiamo deve incrociare il piano/cono. Quelle altre superfici equipotenziali che si vedono nell'immagine che assomigliamo a dei palloni sono limitate
Potrebbe estendere la ricerca anche un paraboloide ellittico (e chi più ne ha più ne metta), basta che sia infinita? Giusto?
[/quote]
Si benissimo.
2) [quote]Domanda per te: cos'e' θ=π/2 ? che superficie e' ?
Fatico a decifrarla, nel senso che se fosse $x=pi/2$ direi un piano di valore sulle ascisse di pi/2, ma ho un theta non un x. In coordinate sferiche mi parrebbe un piano di angolo theta al variare di rho qualunque. non saprei..
[/quote]
Non e' altro che il famoso piano $xy$, che ormai conosciamo a memoria.
Prova a dare un occhio qui
https://it.wikipedia.org/wiki/Sistema_d ... e_sferiche
il "loro" angolo $\theta$ e' il nostro angolo $\theta$.
Non avrei mai immaginato che da un esercizio del genere avrei ottenuto così tatni stimoli. Ne sono piacevolmente colpito
Grazie ancora.
Anche io ne sono colpito. Non era esattamente un "esercizietto".
PS. Ti manca di ricavare il campo elettrico sulla sfera come chiedeva il testo.
Prego...
Sì, ci sono perfettamente anche sulla tua ultima domanda.
Ora mi applico sull'ultima domanda del problema.
Grazie e buona serata
Ora mi applico sull'ultima domanda del problema.
Grazie e buona serata


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo