Energia potenziale di un'asta vincolata ad un estremo
Salve,
risolvendo un'esercizio mi è sorto un dubbio riguardo il calcolo dell'energia potenziale di un'asta obliqua.
L'asta è vincolata per uno degli estremi, ha lunghezza \(\displaystyle d \),massa \(\displaystyle M \) e forma un angolo di \(\displaystyle 45° \) con la normale al pavimento che passa per l'estremo vincolato. La distanza tra l'estremo vincolato dell'asta e il pavimento è di \(\displaystyle 2d \).
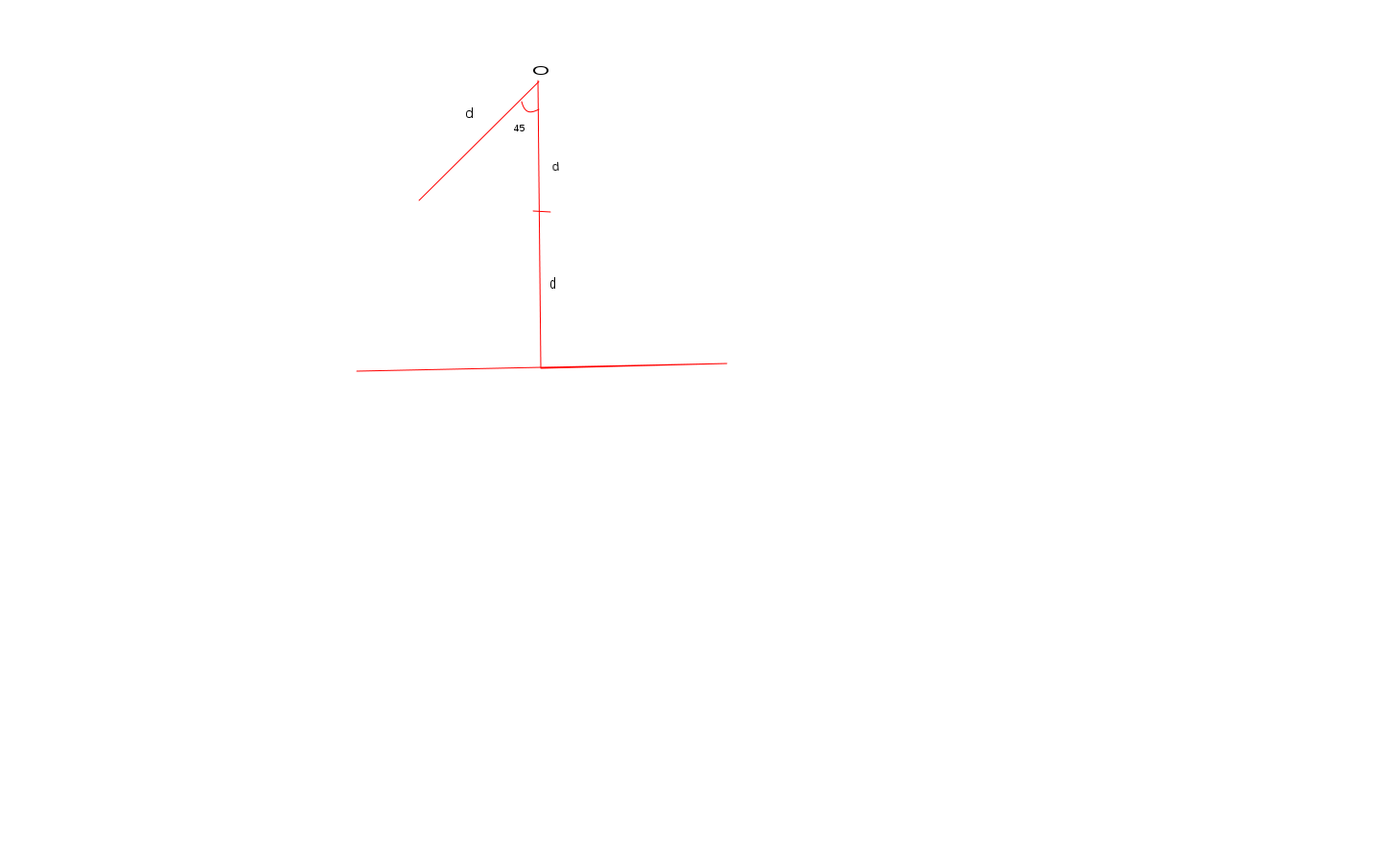
(Scusate l'evidente incapacità grafica)
L'energia potenziale dovrebbe essere \(\displaystyle U= M*g*(distanza.del.centro.di.massa.dal.pavimento) \).
Come posso calcolare la distanza dal pavimento del centro di massa?
Karim19841
risolvendo un'esercizio mi è sorto un dubbio riguardo il calcolo dell'energia potenziale di un'asta obliqua.
L'asta è vincolata per uno degli estremi, ha lunghezza \(\displaystyle d \),massa \(\displaystyle M \) e forma un angolo di \(\displaystyle 45° \) con la normale al pavimento che passa per l'estremo vincolato. La distanza tra l'estremo vincolato dell'asta e il pavimento è di \(\displaystyle 2d \).
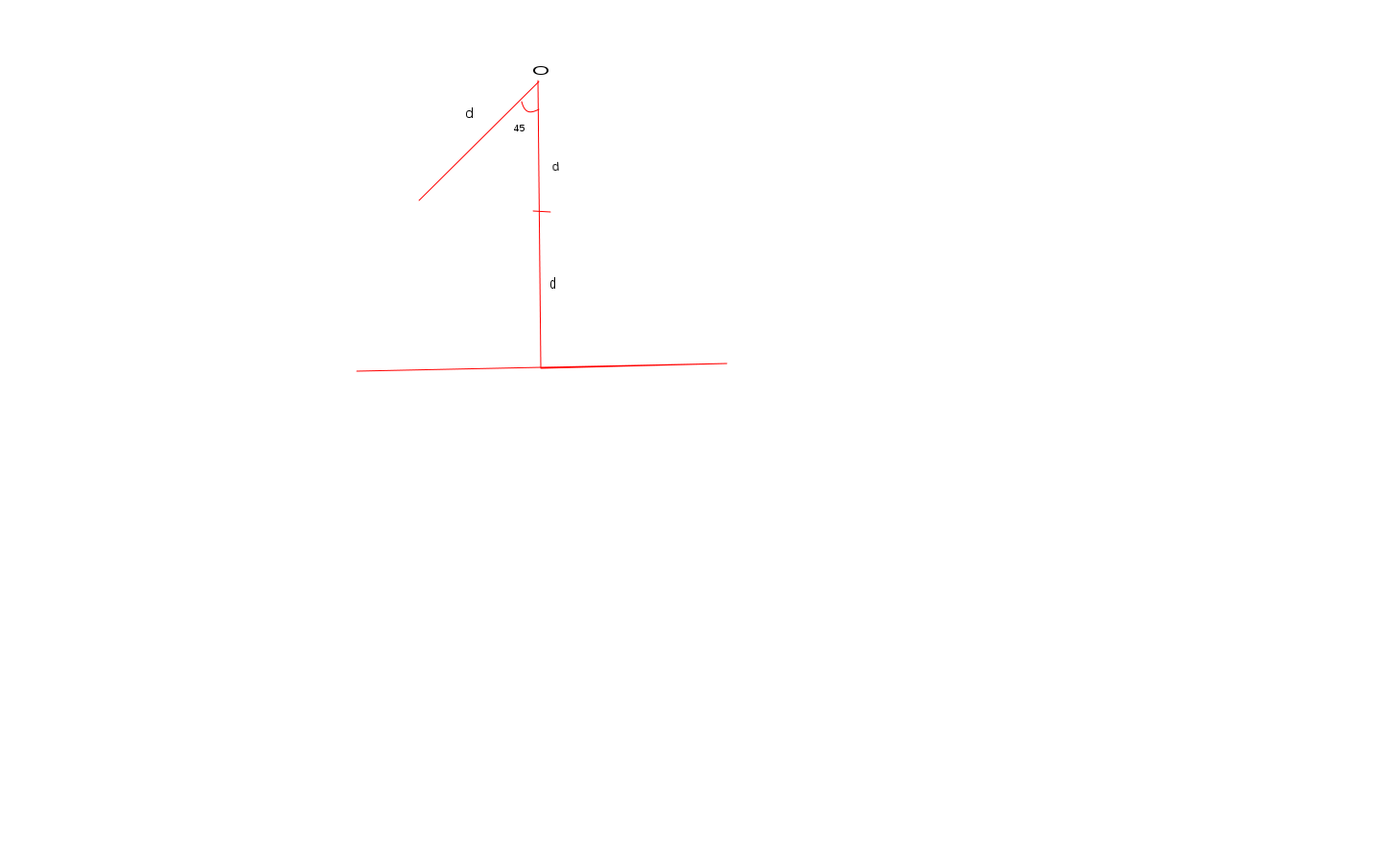
(Scusate l'evidente incapacità grafica)
L'energia potenziale dovrebbe essere \(\displaystyle U= M*g*(distanza.del.centro.di.massa.dal.pavimento) \).
Come posso calcolare la distanza dal pavimento del centro di massa?
Karim19841
Risposte
Sara' data da $2d-Lcos(45)$, no?
"professorkappa":
Sara' data da $2d-Lcos(45)$, no?
Intendevi: $2d-d/2cos(45)$ ?
Si era $L/2$ e non ho notato che $L=d$
Grazie per la risposta,però mi interesserebbe anche capire come ricavare quell'espressione nel caso generale
In quale caso generale? E' un'espressione semplice di quantita' geometriche
Per caso generale intendevo: Come ci si arriva a quell'espressione?
Trigonometria.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo