Due masse e una forza
Un corpo di massa $m=2kg$ poggia su un blocco $M=4kg$.
Il coefficiente di attrito dinamico fra il blocco $M$ e il suolo è $ud=0.2$. Una forza orizzontale $F$ viene applicata al blocco $M$.
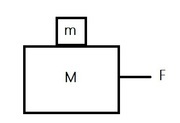
a)Si disegni il diagramma di corpo libero per ciascun blocco.
b)Qual è la forza che accelera la massa $m$?
c)Si calcoli l'intensità della forza necessaria per tirare ambedue i blocchi verso derstra con un'accelerazione $a=3m/s^2$
d)Si determini il minimo valore del coefficiente di attrito statico tra i blocchi in modo che non slitti se l'accelerazione è $3m/s^2$
Diagramma corpo libero:
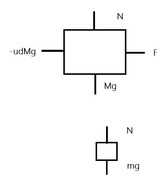
Allora mi blocco dal punto , perchè non riesco a determinare il diagramma delle forze:
$F-ud(m+M)g=M*a_M$ per la massa m non riesco a determinarlo, lo so che è una cavolata ma non c'è attrito, la forza peso è bilanciata dalla reazione vincolare del blocco M, mi perdo in un bicchier d'acqua.
Il coefficiente di attrito dinamico fra il blocco $M$ e il suolo è $ud=0.2$. Una forza orizzontale $F$ viene applicata al blocco $M$.

a)Si disegni il diagramma di corpo libero per ciascun blocco.
b)Qual è la forza che accelera la massa $m$?
c)Si calcoli l'intensità della forza necessaria per tirare ambedue i blocchi verso derstra con un'accelerazione $a=3m/s^2$
d)Si determini il minimo valore del coefficiente di attrito statico tra i blocchi in modo che non slitti se l'accelerazione è $3m/s^2$
Diagramma corpo libero:

Allora mi blocco dal punto , perchè non riesco a determinare il diagramma delle forze:
$F-ud(m+M)g=M*a_M$ per la massa m non riesco a determinarlo, lo so che è una cavolata ma non c'è attrito, la forza peso è bilanciata dalla reazione vincolare del blocco M, mi perdo in un bicchier d'acqua.
Risposte
La massa m in un sistema inerziale tende semplicemente a mantenere la sua velocità iniziale, che è pari a 0. Nel sistema non inerziale del blocco M, invece, la forza che accelera la massa m rispetto al blocco M è una forza apparente che è uguale a:
$ mF/M $ ed ha verso opposto rispetto alla forza F. La richiesta c non l'ho capita per tirare entrambi i blocchi verso destra ci deve essere una forza d'attrito statico tra i blocchi M ed m, ma mi sembra che la presenza di questa forza forza vnega supposta solo nella richiesta d.
$ mF/M $ ed ha verso opposto rispetto alla forza F. La richiesta c non l'ho capita per tirare entrambi i blocchi verso destra ci deve essere una forza d'attrito statico tra i blocchi M ed m, ma mi sembra che la presenza di questa forza forza vnega supposta solo nella richiesta d.
capisco che è come se si trattasse di un passeggero su un'auto e quindi viaggia secondo le velocità dell'auto visto dall'esterno, ma mi potreste aiutare con la parte pratica del problema, perchè non lo so proprio impostare...
Grazie
Grazie
Cominciamo dal punto a) e mi sembra che manchino delle forze ...
Sul blocco piccolo agisce la forza peso del blocco piccolo cioè $P_m=-mg$, la forza normale di reazione del blocco grande $n=+mg$, la forza d'attrito (statico, finchè tiene) che il blocco grande effettua sul blocco piccolo $F_(sm)=mu_s*n=+mu_s*mg$.
Sul blocco grande agiscono la forza del proprio peso $P_M=-Mg$, la forza del peso piccolo $P_m=-mg$, la forza normale di reazione del piano di appoggio $N=+(M+m)g$, la forza esterna orizzontale $F$, la forza di attrito effettuata dal piano sul blocco grande, attrito statico finchè tiene che è pari a $F_(Ms)=-mu_s*N=-mu_s*(M+m)g$ e poi dinamico quando è in movimento, che è pari a $F_(Md)=-mu_d*N=-mu_d*(M+m)g$, ed infine la forza di attrito statico del blocco piccolo sul blocco grande $-F_(sm)=mu_s*n=-mu_s*mg$.
Questo è il punto a.
Prova a proseguire tu ...
Cordialmente, Alex
Sul blocco piccolo agisce la forza peso del blocco piccolo cioè $P_m=-mg$, la forza normale di reazione del blocco grande $n=+mg$, la forza d'attrito (statico, finchè tiene) che il blocco grande effettua sul blocco piccolo $F_(sm)=mu_s*n=+mu_s*mg$.
Sul blocco grande agiscono la forza del proprio peso $P_M=-Mg$, la forza del peso piccolo $P_m=-mg$, la forza normale di reazione del piano di appoggio $N=+(M+m)g$, la forza esterna orizzontale $F$, la forza di attrito effettuata dal piano sul blocco grande, attrito statico finchè tiene che è pari a $F_(Ms)=-mu_s*N=-mu_s*(M+m)g$ e poi dinamico quando è in movimento, che è pari a $F_(Md)=-mu_d*N=-mu_d*(M+m)g$, ed infine la forza di attrito statico del blocco piccolo sul blocco grande $-F_(sm)=mu_s*n=-mu_s*mg$.
Questo è il punto a.
Prova a proseguire tu ...
Cordialmente, Alex
Ma siamo sicuri che ci sia attrito tra le due masse, il testo non ne parla..
-I due corpi si muoveranno con la stessa accelerazione?? Se si perchè?
b) $F_2-u_smg=ma$
$F_2-3.92=0$
$F_2=3.92N$ secondo me sbagliatissimo...
c)${\(F-u_d(M+m)g-u_dmg=Ma),(u_sg=ma):}$
$u_s=3/9.8=0.3$
$F-u_d(M+m)g-u_smg=Ma$
$F-0.2*6*9.8-0.3*2*9.8=12$
$F-11.76-5.38=12$
$F=29.14N$
Secondo me ho sbagliato tutto, ma oramai ci sono abituato...
-I due corpi si muoveranno con la stessa accelerazione?? Se si perchè?
b) $F_2-u_smg=ma$
$F_2-3.92=0$
$F_2=3.92N$ secondo me sbagliatissimo...
c)${\(F-u_d(M+m)g-u_dmg=Ma),(u_sg=ma):}$
$u_s=3/9.8=0.3$
$F-u_d(M+m)g-u_smg=Ma$
$F-0.2*6*9.8-0.3*2*9.8=12$
$F-11.76-5.38=12$
$F=29.14N$
Secondo me ho sbagliato tutto, ma oramai ci sono abituato...
"75america":
Ma siamo sicuri che ci sia attrito tra le due masse, il testo non ne parla..
Concettualmente la forza d'attrito esiste sempre, se poi $mu=0$ allora anche la forza d'attrito sarà pari a zero.
Quindi, visto che concettualmente esiste, io nel diagramma ce la metterei; casomai fossi sicuro che è nulla metterei una nota ...
D'altra parte il punto b) ti chiede qual è la forza che accelera il blocco piccolo; se noi guardiamo il diagramma vediamo che sul blocco piccolo agiscono due forze verticali che si annullano ed una sola forza orizzontale, la forza d'attrito generata dal blocco grande: quindi se il blocco piccolo accelera, lo fa grazie a questa forza. Ovviamente nel caso in cui il coefficiente d'attrito non sia nullo.
Questo è sufficiente per il punto b) in quanto non ti viene chiesta l'intensità di questa forza.
Cordialmente, Alex
Ora veniamo al punto c)
Ti viene chiesta la forza necessaria per accelerare il sistema verso destra, cioè tutti e due i blocchi contemporaneamente. Ora usando la famosa $F_R=M_s*a$, abbiamo che l'accelerazione la conosciamo ($a=3m/s$), la massa del sistema anche $(M_s=M+m)$, mentre la forza risultante $(F_R)$ sarà data dalla somma algebrica delle forze orizzontali (quelle verticale si annullano e non ci interessano direttamente), che sono la forza esterna $F$, la forza d'attrito (dinamico) esercitata dal piano sul blocco grande e le due forze d'attrito tra i due blocchi. Quest'ultime due le possiamo ignorare perchè uguali e contrarie (questa semplificazione, cioè ignorare le forze interne al sistema, si può fare tutte le volte che guardiamo il movimento dell'intero sistema nel suo complesso).
Quindi sarà $F_R=M_s*a$ => $F-F_(mud)=(M+m)*a$ => $F-mud*(M+m)g)=(M+m)*a$ => $F=(M+m)*a-mud*(M+m)g)$
Concludi tu ...
Cordialmente, Alex
Ti viene chiesta la forza necessaria per accelerare il sistema verso destra, cioè tutti e due i blocchi contemporaneamente. Ora usando la famosa $F_R=M_s*a$, abbiamo che l'accelerazione la conosciamo ($a=3m/s$), la massa del sistema anche $(M_s=M+m)$, mentre la forza risultante $(F_R)$ sarà data dalla somma algebrica delle forze orizzontali (quelle verticale si annullano e non ci interessano direttamente), che sono la forza esterna $F$, la forza d'attrito (dinamico) esercitata dal piano sul blocco grande e le due forze d'attrito tra i due blocchi. Quest'ultime due le possiamo ignorare perchè uguali e contrarie (questa semplificazione, cioè ignorare le forze interne al sistema, si può fare tutte le volte che guardiamo il movimento dell'intero sistema nel suo complesso).
Quindi sarà $F_R=M_s*a$ => $F-F_(mud)=(M+m)*a$ => $F-mud*(M+m)g)=(M+m)*a$ => $F=(M+m)*a-mud*(M+m)g)$
Concludi tu ...
Cordialmente, Alex


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo