Due dischi in rotazione
Salve ragazzi, vi propongo un altro quesito che ho quasi per intero capito, ma c'è un dettaglio che mi sfugge e sto ragionandoci su ormai da un pomeriggio. Il problema è il seguente:
Due dischi di ferro, di raggi $R_1 = 0.1 m$ e $R_2 = 2 R_1$ e masse $M_1 = 2kg$ e $M_2 = 1.5 M_1$, sono fissati solidamente uno all'altro in modo tale da risultare coassiali. Essi possono ruotare senza attrito attorno all'asse verticale passante per il centro di massa. Sul disco di raggio $R_1$ è avvolto un filo a cui è appesa la massa $ m= 1kg$. All'istante $t=0$ la massa $m$, inizialmente in quiete, viene lasciata scendere.
a) Calcolare il tempo $t_0$ necessario perchè essa percorra $ h=10 m$.
Sul bordo del disco di raggio $R_2$ è fissato un magnetino di massa $m_0 = 10^-2 kg $ e di dimensioni trascurabili; la forza magnetica che lo tiene attaccato al disco vale $1,5 N$.
b) Dire se al tempo $t_0$ il magnetino è ancora attaccato al disco.
Se si sceglie un sistema di coordinate che ha origine nel centro di massa dell'intero corpo (fatto dai due dischi), si possono calcolare i momenti tenendo conto del fatto che l'unica forza agente sarà la tensione della fune (essendo la forza peso e la reazione vincolare applicate proprio al centro, dunque momento nullo). Ora, il dubbio che mi attanaglia ( e che mi rovina l'intero esercizio) è il seguente:
la massa scende verso il basso, dunque la fune, non appena sarà tesa, causerà una rotazione in senso orario dei dischi. Il verso di un momento è per convenzione positivo quando la rotazione avviene in senso antiorario. Di conseguenza, il momento della tensione non sarà negativo rispetto ad un versore \(\displaystyle \hat{z} \) uscente dal piano di scrittura ?
Due dischi di ferro, di raggi $R_1 = 0.1 m$ e $R_2 = 2 R_1$ e masse $M_1 = 2kg$ e $M_2 = 1.5 M_1$, sono fissati solidamente uno all'altro in modo tale da risultare coassiali. Essi possono ruotare senza attrito attorno all'asse verticale passante per il centro di massa. Sul disco di raggio $R_1$ è avvolto un filo a cui è appesa la massa $ m= 1kg$. All'istante $t=0$ la massa $m$, inizialmente in quiete, viene lasciata scendere.
a) Calcolare il tempo $t_0$ necessario perchè essa percorra $ h=10 m$.
Sul bordo del disco di raggio $R_2$ è fissato un magnetino di massa $m_0 = 10^-2 kg $ e di dimensioni trascurabili; la forza magnetica che lo tiene attaccato al disco vale $1,5 N$.
b) Dire se al tempo $t_0$ il magnetino è ancora attaccato al disco.
Se si sceglie un sistema di coordinate che ha origine nel centro di massa dell'intero corpo (fatto dai due dischi), si possono calcolare i momenti tenendo conto del fatto che l'unica forza agente sarà la tensione della fune (essendo la forza peso e la reazione vincolare applicate proprio al centro, dunque momento nullo). Ora, il dubbio che mi attanaglia ( e che mi rovina l'intero esercizio) è il seguente:
la massa scende verso il basso, dunque la fune, non appena sarà tesa, causerà una rotazione in senso orario dei dischi. Il verso di un momento è per convenzione positivo quando la rotazione avviene in senso antiorario. Di conseguenza, il momento della tensione non sarà negativo rispetto ad un versore \(\displaystyle \hat{z} \) uscente dal piano di scrittura ?
Risposte
Se prendi x diretto verso destra, y diretto verso il basso allora z e' entrante e il momento e' positivo quando il disco gira in senso orario e tagli la testa al toro 

ecco cos'era a sfuggermi. Lo immaginavo ci fosse qualcosa. Ho preso il sistema di coordinate proprio come hai detto tu. Ma come un idiota non ho considerato che così facendo z fosse entrante. Dunque essendo entrante anche il momento, avrà versore parallelo a quello dell'asse z.
Ok. pero' e' una question di lana caprina.
Fai bene a usare una terna levogira sempre, ma in questo caso bastava assegnare il verso positivo alle rotazioni orarie (e di conseguenza anche ai momenti) e finiva li.
Fai bene a usare una terna levogira sempre, ma in questo caso bastava assegnare il verso positivo alle rotazioni orarie (e di conseguenza anche ai momenti) e finiva li.
Ti ringrazio. Mi hai aperto gli occhi. Anche in questo caso mi stavo perdendo in un bicchiere d'acqua.
Mentre ci sono, posto un altro problema che mi sta consumando ogni neurone per come è scritto il testo.
"Su un piano orizzontale è posata una massa m=10kg. Essa viene messa in movimento tramite un filo che si avvolge su una puleggia di raggio r=20cm. Questa è messa in rotazione dalla discesa, sotto l'azione del peso, di una massa M=4kg, a cui è collegata da un filo avvolto su una puleggia R=50cm, coassiale e rigidamente fissata alla precedente. Il momento di inerzia del sistema delle due pulegge rispetto al comune asse di rotazione vale I=6kg m^2. Calcolare:
1)la velocità v di M dopo che è scesa di 1m;
2)le tensioni dei due fili durante il movimento. "
Lo schema è preso da internet ma è quasi uguale a quello presente sul libro (questo è un pò più chiaro).
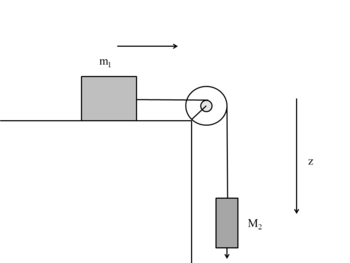
Non ho ben chiaro dal testo come sono disposte le due carrucole. Inoltre, scegliendo anche in questo caso un sistema di coordinate con l'asse y rivolto verso il basso, l'asse x verso destra e l'asse z entrante, se le due carrucole sono rigidamente fissate, dovrebbero ruotare entrambe nello stesso senso, no? e quindi i momenti, assumendo positive le rotazioni orarie, dovrebbero entrambi essere positivi. Cos'è che mi sfugge stavolta?
Mentre ci sono, posto un altro problema che mi sta consumando ogni neurone per come è scritto il testo.
"Su un piano orizzontale è posata una massa m=10kg. Essa viene messa in movimento tramite un filo che si avvolge su una puleggia di raggio r=20cm. Questa è messa in rotazione dalla discesa, sotto l'azione del peso, di una massa M=4kg, a cui è collegata da un filo avvolto su una puleggia R=50cm, coassiale e rigidamente fissata alla precedente. Il momento di inerzia del sistema delle due pulegge rispetto al comune asse di rotazione vale I=6kg m^2. Calcolare:
1)la velocità v di M dopo che è scesa di 1m;
2)le tensioni dei due fili durante il movimento. "
Lo schema è preso da internet ma è quasi uguale a quello presente sul libro (questo è un pò più chiaro).

Non ho ben chiaro dal testo come sono disposte le due carrucole. Inoltre, scegliendo anche in questo caso un sistema di coordinate con l'asse y rivolto verso il basso, l'asse x verso destra e l'asse z entrante, se le due carrucole sono rigidamente fissate, dovrebbero ruotare entrambe nello stesso senso, no? e quindi i momenti, assumendo positive le rotazioni orarie, dovrebbero entrambi essere positivi. Cos'è che mi sfugge stavolta?
Le 2 carrucole sono coassiali e rigidamente collegate (saldate).
Nel sdr scelto da te, le rotazioni sono positive in S.O.
Quindi quando scrivi le equazioni di momento, i momenti che tendono a far girare in S.O sono positivi.
Quindi per la carrucola, l'equazione e' $T_2R-T_1r=Iddottheta$
Per il corpo 2: $M_2g-T_2=M_2a_2=M_2Rddottheta$
Per il corpo 1: $T_1=m_1a_1=m_1rddottheta$
3 equazioni nelle incongite $T_1, T_2$ e $ddottheta$.
Nota $ddottheta$, e' possibile, cinematicamente, trovare la velocita' dopo che il corpo ha percorso $h$.
Oppure, conservando l'energia meccanica, che, se supponiamo nulla l'energia potenziale all'istante iniziale, e' nulla perche il sistema parte da fermo
$0=1/2Idottheta^2+1/2m_1v_1^2+1/2M_2v_2^2-M_2gh$
Dove ovviamente $v_1=rdottheta$ e $v_2=Rdottheta$
Nel sdr scelto da te, le rotazioni sono positive in S.O.
Quindi quando scrivi le equazioni di momento, i momenti che tendono a far girare in S.O sono positivi.
Quindi per la carrucola, l'equazione e' $T_2R-T_1r=Iddottheta$
Per il corpo 2: $M_2g-T_2=M_2a_2=M_2Rddottheta$
Per il corpo 1: $T_1=m_1a_1=m_1rddottheta$
3 equazioni nelle incongite $T_1, T_2$ e $ddottheta$.
Nota $ddottheta$, e' possibile, cinematicamente, trovare la velocita' dopo che il corpo ha percorso $h$.
Oppure, conservando l'energia meccanica, che, se supponiamo nulla l'energia potenziale all'istante iniziale, e' nulla perche il sistema parte da fermo
$0=1/2Idottheta^2+1/2m_1v_1^2+1/2M_2v_2^2-M_2gh$
Dove ovviamente $v_1=rdottheta$ e $v_2=Rdottheta$
"professorkappa":
Quindi per la carrucola, l'equazione e' $T_2R-T_1r=Iddottheta$
Ciao Kappa, se i due momenti sono positivi perchè poi si vanno a sottrarre nella II equazione cardinale?
Perche' $T_1$ e' positivo, $T_2$ e' negativo (regola della mano dx oppure noti che e' diretto verso sinistra,cioe' tende a far ruotare la carrucola in S.A.O.
Correggimi se sbaglio, la tensione \(\displaystyle T_1 \) farebbe ruotare l'intera carrucola in senso A.O. se il corpo \(\displaystyle m_1 \) si muovesse verso sinistra. Ma il corpo in questione è poggiato su un piano orizzontale e si muove verso destra essendo tirato dal corpo in discesa verticalmente. Dove sbaglio?
Edit: credo di aver capito. Nel calcolo dei momenti, devo studiare il verso del vettore momento come se quella forza agisse realmente sulla carrucola.
Un'ultima cosa vorrei approfondire: il verso "preponderante" della rotazione lo impongo io oppure mi adatto in base a come si muoverà il sistema? mi spiego meglio. Nel primo caso, quello dei dischi, la massa appesa scendeva verso il basso costringendo il sistema a ruotare in senso orario (quindi abbiamo preso un sistema di coordinate con z entrante). Nel caso delle due masse attorno a una carrucola, anche in questo caso è la massa appesa a far ruotare le pulegge in senso orario. Se avessimo una carrucola con due masse entrambe appese verticalmente, e la massa di sinistra scendesse verso il basso, il sistema ruoterebbe "spontaneamente" in modo antiorario. Quindi considererei positive le rotazioni in senso antiorario. E' un buon criterio?
Edit: credo di aver capito. Nel calcolo dei momenti, devo studiare il verso del vettore momento come se quella forza agisse realmente sulla carrucola.
Un'ultima cosa vorrei approfondire: il verso "preponderante" della rotazione lo impongo io oppure mi adatto in base a come si muoverà il sistema? mi spiego meglio. Nel primo caso, quello dei dischi, la massa appesa scendeva verso il basso costringendo il sistema a ruotare in senso orario (quindi abbiamo preso un sistema di coordinate con z entrante). Nel caso delle due masse attorno a una carrucola, anche in questo caso è la massa appesa a far ruotare le pulegge in senso orario. Se avessimo una carrucola con due masse entrambe appese verticalmente, e la massa di sinistra scendesse verso il basso, il sistema ruoterebbe "spontaneamente" in modo antiorario. Quindi considererei positive le rotazioni in senso antiorario. E' un buon criterio?
Per il calcolo dei momenti, devi idealmente spezzare la corda. La tensione e' verso sinistra (il blocco si oppone al movimento verso destra). Tutte le volte che hai una fune, la tensione "esce" dallo spezzone nel punto di taglio ideale. Quindi per lo spezzone di fune attaccato al blocco, la tensione e' diretta verso destra. Per la parte di corda attorno alla carrucola, la tensione e' verso sx e quindi fa momento negativo.
Stessa cosa per il blocco appeso, se tagli in un punto compreso fra il blocco e la carrucola: la tensione che fa ruotare la carrucola e' verso il basso, mentre la stessa tensione trattiene il blocco ed e'diretta verso l'alto.
Non esiste un verso preponderante. Esiste un sistema di riferimento che ti fa mettere i segni congruenti e le incognite si mettono normalmente concordi con quel sistema di riferimento. Alla fine della risoluzione del sistema, le incognite avranno un segno. Se positivo, vuol dire che sono concordi con il sistema, altrimenti sono opposte al sistema.
In questo esercizio, siccome sai che scendera', ti conviene assegnare il verso positivo A.O. Vedrai che $ddottheta$ ti verra' positivo. Se ti dovesse venire negativo, hai sbagliato da qualche parte.
Ma se non sai a priori come ruota la carrucola gli devi dare un verso e sperare di non fare errori di calcolo, perche il segno positivo ti assicurera' che il verso scelto da te a priori e' "giusto".
Stessa cosa per il blocco appeso, se tagli in un punto compreso fra il blocco e la carrucola: la tensione che fa ruotare la carrucola e' verso il basso, mentre la stessa tensione trattiene il blocco ed e'diretta verso l'alto.
Non esiste un verso preponderante. Esiste un sistema di riferimento che ti fa mettere i segni congruenti e le incognite si mettono normalmente concordi con quel sistema di riferimento. Alla fine della risoluzione del sistema, le incognite avranno un segno. Se positivo, vuol dire che sono concordi con il sistema, altrimenti sono opposte al sistema.
In questo esercizio, siccome sai che scendera', ti conviene assegnare il verso positivo A.O. Vedrai che $ddottheta$ ti verra' positivo. Se ti dovesse venire negativo, hai sbagliato da qualche parte.
Ma se non sai a priori come ruota la carrucola gli devi dare un verso e sperare di non fare errori di calcolo, perche il segno positivo ti assicurera' che il verso scelto da te a priori e' "giusto".


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo