Dubbio integrale capacità condensatore cilindrico
Ciao, mi sono trovato davanti ad un dubbio durante il calcolo della capacità di un condensatore cilindrico (di raggio interno R1, raggio esterno R2, alto L, con L>>R2 e carico Q):
Vi spiego il mio ragionamento:

Uso la relazione C=Q/(Va-Vb)
Calcolo tramite il teorema di gauss il campo elettrico fra i due conduttori ed ottengo:
$ vec(E)=Q/(2*pi*r*L*epsi)*hat(r) $
poi tramite $ dV=-vec(E)*vec(dr) $ calcolo la differenza di potenziale, io per convenzione uso integrare dall'armatura negativa a quella positiva.
Ottenendo:
$ int_(V(R2))^(V(R1)) dV =-int_((R2))^((R1)) vec(E)*vec(dr)= -int_((R2))^((R1))Q/(2*pi*r*L*epsi)*hat(r)*vec(dr) $
ora ho pensato il prodotto scalare $ hat(r)*vec(dr) $ mi da come risultato $ -dr $ poiché se mi muovo da R2 ad R1 i due vettori sono in "antiparallelo", quindi il loro angolo è di 180°.
giungo quindi alla fine del conto a:
$ V(R1)-V(R2)=Q/(2*pi*L*epsi)*ln((R1)/(R2)) $ ma dovrei giungere a $ V(R1)-V(R2)=Q/(2*pi*L*epsi)*ln((R2)/(R1)) $
Ora se a questo punto $ int_(V(R2))^(V(R1)) dV = -int_((R2))^((R1))Q/(2*pi*r*L*epsi)*hat(r)*vec(dr) $ tolgo il meno e inverto gli estremi dell'integrale mi trovo che il prodotto scalare vale $ hat(r)*vec(dr) = dr $ poiché mi sposto da R1 ad R2 ed il campo elettrico e lo spostamento sono concordi.
Facendo così giungo alla fine al risultato corretto, sapete dirmi il perché?
Io ho pensato perché l'integrale definito per definizione deve avere l'estremo inferiore minore dell'estremo superiore, e prima di fare il prodotto scalare devo pormi in questa condizione.
Aspetto vostri parere
Vi spiego il mio ragionamento:

Uso la relazione C=Q/(Va-Vb)
Calcolo tramite il teorema di gauss il campo elettrico fra i due conduttori ed ottengo:
$ vec(E)=Q/(2*pi*r*L*epsi)*hat(r) $
poi tramite $ dV=-vec(E)*vec(dr) $ calcolo la differenza di potenziale, io per convenzione uso integrare dall'armatura negativa a quella positiva.
Ottenendo:
$ int_(V(R2))^(V(R1)) dV =-int_((R2))^((R1)) vec(E)*vec(dr)= -int_((R2))^((R1))Q/(2*pi*r*L*epsi)*hat(r)*vec(dr) $
ora ho pensato il prodotto scalare $ hat(r)*vec(dr) $ mi da come risultato $ -dr $ poiché se mi muovo da R2 ad R1 i due vettori sono in "antiparallelo", quindi il loro angolo è di 180°.
giungo quindi alla fine del conto a:
$ V(R1)-V(R2)=Q/(2*pi*L*epsi)*ln((R1)/(R2)) $ ma dovrei giungere a $ V(R1)-V(R2)=Q/(2*pi*L*epsi)*ln((R2)/(R1)) $
Ora se a questo punto $ int_(V(R2))^(V(R1)) dV = -int_((R2))^((R1))Q/(2*pi*r*L*epsi)*hat(r)*vec(dr) $ tolgo il meno e inverto gli estremi dell'integrale mi trovo che il prodotto scalare vale $ hat(r)*vec(dr) = dr $ poiché mi sposto da R1 ad R2 ed il campo elettrico e lo spostamento sono concordi.
Facendo così giungo alla fine al risultato corretto, sapete dirmi il perché?
Io ho pensato perché l'integrale definito per definizione deve avere l'estremo inferiore minore dell'estremo superiore, e prima di fare il prodotto scalare devo pormi in questa condizione.
Aspetto vostri parere
Risposte
Un momento.
Se ti chiedo di calcolare
$\int_2^1 x\ dx$
mi rispondi
$x^2/2 ]_2^1 = -3/2$.
Il risultato e' negativo, ma non hai dovuto fare delle considerazioni tipo: allora $dx$ diventa $-dx$ perche' mi muovo da 2 a 1.
Eppure muovendosi da 2 a 1 si percorre l'asse x nel verso contrario.
L'errore e' nel cambiare $dr$ in $-dr$.
Spero sia chiaro.
Se ti chiedo di calcolare
$\int_2^1 x\ dx$
mi rispondi
$x^2/2 ]_2^1 = -3/2$.
Il risultato e' negativo, ma non hai dovuto fare delle considerazioni tipo: allora $dx$ diventa $-dx$ perche' mi muovo da 2 a 1.
Eppure muovendosi da 2 a 1 si percorre l'asse x nel verso contrario.
L'errore e' nel cambiare $dr$ in $-dr$.
Spero sia chiaro.
Ciao, CREDO che il contesto che mi esponi sia diverso dal mio, cerco di spiegarmi meglio.
Nel caso che mi esponi tu non c'è un prodotto scalare all'interno dell'integrale.
Nel tuo caso sono d'accordo con ciò che dici.
Nel mio caso, io ho un prodotto scalare ( $ hat(r)*vec(dr) $ ) e a seconda che mi muova in verso opposto o contrario al campo elettrico mi cambia il segno del prodotto scalare. Ed il verso in cui mi muovo non è determinato proprio dagli estremi dell'integrale ?
Spero di essermi espresso correttamente.
Buona serata!
Nel caso che mi esponi tu non c'è un prodotto scalare all'interno dell'integrale.
Nel tuo caso sono d'accordo con ciò che dici.
Nel mio caso, io ho un prodotto scalare ( $ hat(r)*vec(dr) $ ) e a seconda che mi muova in verso opposto o contrario al campo elettrico mi cambia il segno del prodotto scalare. Ed il verso in cui mi muovo non è determinato proprio dagli estremi dell'integrale ?
Spero di essermi espresso correttamente.
Buona serata!
"matteo_g":
Nel mio caso, io ho un prodotto scalare ( $ hat(r)*vec(dr) $ ) e a seconda che mi muova in verso opposto o contrario al campo elettrico mi cambia il segno del prodotto scalare. Ed il verso in cui mi muovo non è determinato proprio dagli estremi dell'integrale ?
Il $\vec {dr}$ non e' un vettore che orienti come vuoi tu e lungo come vuoi tu.
Il $\vec {dr}$ e' una "freccina" che ti da la direzione e l'intensità con cui varia il vettore raggio.
Ad es, il raggio che va dal centro a (1,0), quando ha una variazione positiva (si allunga), si allunga nella direzione dell'asse x.
Quindi in (1,0) metto una freccina $\vec {dr}$ orientata come l'asse x e di intensità 1.
Intensità 1 perchè sto considerando un differenziale.
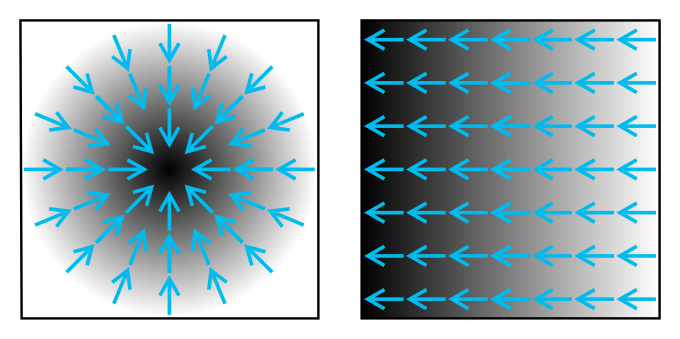
Quindi in tutto il piano cartesiano dovresti immaginare tante freccine $\vec dr$ che sono disposte a raggiera, uno per ogni punto dl piano. Quindi ne hai infiniti.
Una cosa del genere(vedi figura) (quello a sinistra ma con le freccine nel verso opposto).
Ovvero se stabilisci un sistema di coordinate polari $(r, \theta)$, allora il campo vettoriale $\vec dr$ e' obbligato, stabilito.
Non ha senso, come hai scritto, che $\hat r \cdot \vec {dr}$ hanno versi opposti e quindi cambi il segno ecc, ecc.
Hai sempre e solo che $\hat r \cdot \vec {dr} =dr$.
Infatti nell'integrale se sostituisci $\hat r \cdot \vec {dr} =dr$ hai il risultato corretto.
Buongiorno, dalla tua spiegazione confermo le mie forti lacune in analisi matematica.
Per quanto riguarda la tua risposta invece, ho alcune considerazioni al riguardo:
1) Come si chiama esattamente l'argomento di cui mi stai parlando? Perché sul libro di analisi fatico a trovare esattamente questo argomento.
2) Sono d'accordo che il verso di $ hat(r) $ sia "fisso", nel mio caso l'ho posto verso l'esterno del cilindro.
Per quanto riguarda $ vec(dr) $ ho qualche dubbio ancora, per me questo dr era uno spostamento infinitesimo.
Ora se io eseguo il prodotto scalare $ hat(r)*vec(dr)=abs(r)*abs(dr)*cos(alpha)=1*dr*cos(alpha) $.
Se io integro da R2 ad R1 non significa che mi sposto di piccoli passi "dr" da R2 fino a raggiungere R1?
Quindi otterrei:

Nel caso mi spostassi da R1 a R2 invece:

3) Quindi secondo te tutto ciò che ho scritto al punto 2 è completamente errato, giusto?
se ho capito bene cosa intendi: l'orientazione di $ vec(dr) $ non dipende quindi dagli estremi che pongo agli integrali (come ciò che ho evidenziato in figura) ma solamente da come varia il vettore raggio nello spazio?
Per quanto riguarda la tua risposta invece, ho alcune considerazioni al riguardo:
1) Come si chiama esattamente l'argomento di cui mi stai parlando? Perché sul libro di analisi fatico a trovare esattamente questo argomento.
2) Sono d'accordo che il verso di $ hat(r) $ sia "fisso", nel mio caso l'ho posto verso l'esterno del cilindro.
Per quanto riguarda $ vec(dr) $ ho qualche dubbio ancora, per me questo dr era uno spostamento infinitesimo.
Ora se io eseguo il prodotto scalare $ hat(r)*vec(dr)=abs(r)*abs(dr)*cos(alpha)=1*dr*cos(alpha) $.
Se io integro da R2 ad R1 non significa che mi sposto di piccoli passi "dr" da R2 fino a raggiungere R1?
Quindi otterrei:

Nel caso mi spostassi da R1 a R2 invece:

3) Quindi secondo te tutto ciò che ho scritto al punto 2 è completamente errato, giusto?
se ho capito bene cosa intendi: l'orientazione di $ vec(dr) $ non dipende quindi dagli estremi che pongo agli integrali (come ciò che ho evidenziato in figura) ma solamente da come varia il vettore raggio nello spazio?
Ciò di cui ti ha parlato è in generale la teoria delle forme differenziali e varietà differenziabili. Più in piccolo puoi cercarla come curve e superfici in $R^3$ , campi vettoriali , integrali di linea e di superficie. Sono cose che in genere si fanno tra analisi 2 e 3.
Ok, grazie. Potresti dare un'occhiata alla domanda 2 ? 
Ti ridarei la stessa risposta data da Quinzio la prima volta. Se inverti l'intervallo di integrazione ti esce un segno $-$ ovviamente perché percorri il segmento al contrario, ma il $dr$ è fisso. Per farla breve la convenzione vuole che nelle formule di integrazione (formule di divergenza, rotore etc) le curve siano orientate (da qui il verso del elemento infinitesimo) in modo da tenere il dominio a sinistra; l'orientazione delle superfici è fatta in modo da avere il segno positivo alla normale uscente. Chiaramente puoi cambiare convenzione ma è meglio non confondersi.
Sempre al riguardo, mi date la conferma che ho capito bene
Supponiamo di avere una particella di carica q e massa m che viene lanciata verso una lastra con densità volumetrica $ rho $ uniformemente carica.
Il tutto orientato come in figura.

Se io voglio calcolare il lavoro svolto dal campo elettrico quando la particella si sposta da 2a ad a:
\( dL=\overrightarrow{F} \cdot \overrightarrow{dl} \)
\( dL=\overrightarrow{F} \cdot \overrightarrow{dl} =q\cdot \overrightarrow{E}\cdot \overrightarrow{dl} \)
\( L=\int_{2a}^{a} q\cdot \overrightarrow{E}\cdot \overrightarrow{dl} =\int_{2a}^{a} q\cdot E\cdot dl \)
Con angolo fra E e dl pari a zero e non 180 anche se l'integrale va da 2a ad a, ovvero "contro le x crescenti"
Mi confermate che sia così?
Supponiamo di avere una particella di carica q e massa m che viene lanciata verso una lastra con densità volumetrica $ rho $ uniformemente carica.
Il tutto orientato come in figura.

Se io voglio calcolare il lavoro svolto dal campo elettrico quando la particella si sposta da 2a ad a:
\( dL=\overrightarrow{F} \cdot \overrightarrow{dl} \)
\( dL=\overrightarrow{F} \cdot \overrightarrow{dl} =q\cdot \overrightarrow{E}\cdot \overrightarrow{dl} \)
\( L=\int_{2a}^{a} q\cdot \overrightarrow{E}\cdot \overrightarrow{dl} =\int_{2a}^{a} q\cdot E\cdot dl \)
Con angolo fra E e dl pari a zero e non 180 anche se l'integrale va da 2a ad a, ovvero "contro le x crescenti"
Mi confermate che sia così?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo