Differenza di potenziale tra due punti in un campo elettrico
Ciao a tutti, ho alcuni dubbi riguardo la risoluzione del seguente esercizio.
Una carica puntiforme positiva $Q = + 6×10^-7 C $ è fissa nell’origine del sistema di riferimento. Una lastra piana infinita carica negativamente con densità uniforme $σ = -2 × 10^-7 C/m^2$ è posta in x = d = 1.3 m.
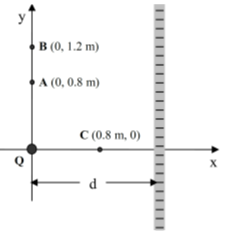
Il primo punto mi chiede: modulo e direzione (angolo rispetto all’asse x) del campo elettrico risultante nel punto A che ho risolto nel seguente modo:
Ho calcolato $E_Q = Q/(4pi*epsilon*r^2)$ e $E_sigma = sigma / (2*epsilon)$
Li ho sommati vettorialmente e mi ritrovo $|E| = 14,1 (kN)/C$ con un angolo di circa 37 gradi rispetto all'asse x.
Il secondo: la differenza di potenziale tra i punti A e B
La differenza di potenziale dovuta alla carica Q è data da $Va - Vb = (Q/(4pi*epsilon*r^2))*(1/r_a - 1/r_b)$
Invece quella dovuta al piano è nulla poiche il vettore spostamento e il vettore $E_sigma$ sono perpendicolari, giusto?
Prima di porre gli altri quesiti vorrei sapere se questi primi 2 punti sono stati svolti correttamente, perchè ho molti dubbi anche su questi. Grazie mille!
Una carica puntiforme positiva $Q = + 6×10^-7 C $ è fissa nell’origine del sistema di riferimento. Una lastra piana infinita carica negativamente con densità uniforme $σ = -2 × 10^-7 C/m^2$ è posta in x = d = 1.3 m.

Il primo punto mi chiede: modulo e direzione (angolo rispetto all’asse x) del campo elettrico risultante nel punto A che ho risolto nel seguente modo:
Ho calcolato $E_Q = Q/(4pi*epsilon*r^2)$ e $E_sigma = sigma / (2*epsilon)$
Li ho sommati vettorialmente e mi ritrovo $|E| = 14,1 (kN)/C$ con un angolo di circa 37 gradi rispetto all'asse x.
Il secondo: la differenza di potenziale tra i punti A e B
La differenza di potenziale dovuta alla carica Q è data da $Va - Vb = (Q/(4pi*epsilon*r^2))*(1/r_a - 1/r_b)$
Invece quella dovuta al piano è nulla poiche il vettore spostamento e il vettore $E_sigma$ sono perpendicolari, giusto?
Prima di porre gli altri quesiti vorrei sapere se questi primi 2 punti sono stati svolti correttamente, perchè ho molti dubbi anche su questi. Grazie mille!
Risposte
SI, è tutto corretto.
In particolare per il piano le linee equipotenziali sono le rette parallele all'asse y.
In particolare per il piano le linee equipotenziali sono le rette parallele all'asse y.
Grazie mille!
Il terzo punto mi chiede invece la differenza di potenziale tra i punti A e C
La differenza di potenziale dovuta a Q l'ho calcolata come prima cambiando i valori delle distanze. Mentre quella dovuta al piano, essendo E costante è pari a $\Delta V = - E*d*cos(theta)$.
In questo caso la distanza d si calcola col teorema di Pitagora e l'angolo theta sarà 45 gradi? Quindi $\Delta V = - E*d*sqrt(2)/2$? E una volta che ho le due differenze di potenziale, come vanno trattate? Basta fare la somma algebrica?
Il terzo punto mi chiede invece la differenza di potenziale tra i punti A e C
La differenza di potenziale dovuta a Q l'ho calcolata come prima cambiando i valori delle distanze. Mentre quella dovuta al piano, essendo E costante è pari a $\Delta V = - E*d*cos(theta)$.
In questo caso la distanza d si calcola col teorema di Pitagora e l'angolo theta sarà 45 gradi? Quindi $\Delta V = - E*d*sqrt(2)/2$? E una volta che ho le due differenze di potenziale, come vanno trattate? Basta fare la somma algebrica?
Per il calcolo del potenziale in C dovuto al piano tieni conto che le linee equipotenziali sono parallele all'asse y ovvero al piano e quindi ..
Guarda anche questo post
https://www.matematicamente.it/forum/vi ... 9&t=227091
Invece per il calcolo della differenza basta la differenza algebrica perchè stiamo parlando di una grandezza scalare e idem per le somme.
Guarda anche questo post
https://www.matematicamente.it/forum/vi ... 9&t=227091
Invece per il calcolo della differenza basta la differenza algebrica perchè stiamo parlando di una grandezza scalare e idem per le somme.
Quindi per il potenziale in C dovuto al piano posso considerare piu semplicemente il punto A in (0;0). Mentre quello dovuto alla carica Q è nullo essendo i punti equidistanti dall'origine?
Esatto 

Ti ringrazio 


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo