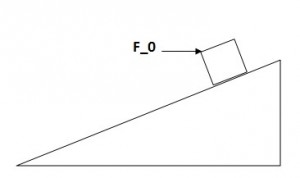
Corpo su piano inclinato sottoposto a forza orizzontale
Un corpo di massa 10kg, posto su un piano inclinato di 30° con l'orizzontale con un coefficiente d'attrito di 0.2, è spinto da una forza orizzontale fo. Calcolare il valore di fo per il quale il corpo sale con velocità costante. Calcolare il lavoro fatto da fo in 10s.
$F_O-mgsentheta-udmgcostheta=0$
$F_O=49+19.6*0.866=65.97N$
Ma il lavoro non riesco a calcolarmelo, perchè il teorema dell'energia cinetica parla di risultante delle forze agenti sul corpo ma è 0

$F_O-mgsentheta-udmgcostheta=0$
$F_O=49+19.6*0.866=65.97N$
Ma il lavoro non riesco a calcolarmelo, perchè il teorema dell'energia cinetica parla di risultante delle forze agenti sul corpo ma è 0
Risposte
Ti si chiede solo il lavoro fatto da $F_O$ non dalla risultante ... e il segno nella prima formula è sbagliato (infatti il calcolo l'hai fatto giusto  )
)
Cordialmente, Alex
 )
)Cordialmente, Alex
Alex ho corretto la prima formula, errore di battitura, ma se il corpo si muove con velocità costante
quando applico la legge oraria del moto rett unif $x(t)=x_0+v(t)$, ho come incognita sia la velocità che lo spazio, pur conoscendo il tempo
quando applico la legge oraria del moto rett unif $x(t)=x_0+v(t)$, ho come incognita sia la velocità che lo spazio, pur conoscendo il tempo
Mi sto scervellando da un po pure io sulla seconda parte dell'esercizio...qualcuno sa consigliarmi se avete capito il modo ?? Grazie
Ho diversi dubbi:
1-Se il corpo è spinto, vuol dire che questo non parte da fermo giusto? Perchè se partisse da fermo e poi per calcolarci la Forza $F_0$ nell'equazione impostiamo $a=0$
2-Quando provo a calcolare il lavoro Fatto da $F_O$ in $10s$, io dovrei conoscere lo spazio percorso in 10sec a velocità costante,ma non so come fare.
Poi non posso calcolare la velocità nemmeno con la conservazione dell'energia meccanica, per la presenza della forza d'attrito, non conservativa.
Ho provato così:
$\Delta_K=L_(peso)+L_(reaz.vinc)+L_(attri)$, ma non so a che strada mi porti
Spero nel vostro aiuto, sto impazzendo
1-Se il corpo è spinto, vuol dire che questo non parte da fermo giusto? Perchè se partisse da fermo e poi per calcolarci la Forza $F_0$ nell'equazione impostiamo $a=0$
2-Quando provo a calcolare il lavoro Fatto da $F_O$ in $10s$, io dovrei conoscere lo spazio percorso in 10sec a velocità costante,ma non so come fare.
Poi non posso calcolare la velocità nemmeno con la conservazione dell'energia meccanica, per la presenza della forza d'attrito, non conservativa.
Ho provato così:
$\Delta_K=L_(peso)+L_(reaz.vinc)+L_(attri)$, ma non so a che strada mi porti
Spero nel vostro aiuto, sto impazzendo
"75america":
Un corpo di massa 10kg, posto su un piano inclinato di 30° con l'orizzontale con un coefficiente d'attrito di 0.2, è spinto da una forza orizzontale fo. Calcolare il valore di fo per il quale il corpo sale con velocità costante. Calcolare il lavoro fatto da fo in 10s.

$F_O-mgsentheta-udmgcostheta=0$
$F_O=49+19.6*0.866=65.97N$
Ma il lavoro non riesco a calcolarmelo, perchè il teorema dell'energia cinetica parla di risultante delle forze agenti sul corpo ma è 0
La soluzione che dai ($F_0-mgsentheta-udmgcostheta=0$" e' completamente sballata,
La soluzione corretta e' \( F_0 = \frac{mgsin \vartheta +\mu mg\cos \vartheta }{\cos \vartheta -\mu \sin \vartheta } \)
Non ti scervellare con la ricerca del lavoro fatto da $F_0$, perche, per come e' impostato il problema, non si puo' risolvere (manca la velocita' o lo spostamento in 10 secondi).
Non va bene.
La forza $F_O$ ha una componente parallela al piano $F_P = F_O cos \theta$ e una componente perpendicolare al piano $F_N = F_Osen\theta$ , la quale preme sul piano e quindi aumenta la reazione normale del piano sul corpo, che ammonta in modulo a :
$mgcos\theta + F_Osen\theta$.
Percio la forza di attrito, resistente, diretta verso il basso, vale in modulo: $F_a = \mu(mgcos\theta + F_Osen\theta)$
Inoltre c'è ancora la componente del peso, resistente, diretta verso il basso , data in modulo da : $mgsen\theta$
Pertanto, il moto avviene a velocità costante quando : $F_O cos \theta - \mu(mgcos\theta + F_Osen\theta)-mgsen\theta = 0 $
Il che vuol dire : $F_O = (\mu(mgcos\theta + F_Osen\theta)+mgsen\theta)/(cos\theta) $
Il lavoro si può calcolare solo se si sa lo spostamento in 10 s, quindi sono d'accordo che con i dati del problema non è possibile.
La forza $F_O$ ha una componente parallela al piano $F_P = F_O cos \theta$ e una componente perpendicolare al piano $F_N = F_Osen\theta$ , la quale preme sul piano e quindi aumenta la reazione normale del piano sul corpo, che ammonta in modulo a :
$mgcos\theta + F_Osen\theta$.
Percio la forza di attrito, resistente, diretta verso il basso, vale in modulo: $F_a = \mu(mgcos\theta + F_Osen\theta)$
Inoltre c'è ancora la componente del peso, resistente, diretta verso il basso , data in modulo da : $mgsen\theta$
Pertanto, il moto avviene a velocità costante quando : $F_O cos \theta - \mu(mgcos\theta + F_Osen\theta)-mgsen\theta = 0 $
Il che vuol dire : $F_O = (\mu(mgcos\theta + F_Osen\theta)+mgsen\theta)/(cos\theta) $
Il lavoro si può calcolare solo se si sa lo spostamento in 10 s, quindi sono d'accordo che con i dati del problema non è possibile.
"navigatore":
Non va bene.
La forza $F_O$ ha una componente parallela al piano $F_P = F_O cos \theta$ e una componente perpendicolare al piano $F_N = F_Osen\theta$ , la quale preme sul piano e quindi aumenta la reazione normale del piano sul corpo, che ammonta in modulo a :
$mgcos\theta + F_Osen\theta$.
Percio la forza di attrito, resistente, diretta verso il basso, vale in modulo: $F_a = \mu(mgcos\theta + F_Osen\theta)$
Inoltre c'è ancora la componente del peso, resistente, diretta verso il basso , data in modulo da : $mgsen\theta$
Pertanto, il moto avviene a velocità costante quando : $F_O cos \theta - \mu(mgcos\theta + F_Osen\theta)-mgsen\theta = 0 $
Il che vuol dire : $F_O = (\mu(mgcos\theta + F_Osen\theta)+mgsen\theta)/(cos\theta) $
Il lavoro si può calcolare solo se si sa lo spostamento in 10 s, quindi sono d'accordo che con i dati del problema non è possibile.
Navigatore, attento, stai esprimendo $F_0$ in funzione di $F_0$.
Se raccogli $F_0$ arrivi alla mia soluzione.
PK
Hai ragione tu PK, ho mancato il passaggio finale per isolare $F_O$ .
Comunque il ragionamento per 75america è quello.
Comunque il ragionamento per 75america è quello.
Eh, lo so, e' quello che ho fatto io, tanto e' vero che il risultato e' lo stesso (a meno dell'errorino che hai fatto su $F_0$).
Pero' se glieli risolvi tu.......quando imparano sti ragazzi?
Pero' se glieli risolvi tu.......quando imparano sti ragazzi?
-Vi ringrazio per le risposte, così ho capito il problema,in effetti avevo il dubbio che la forza pur essendo orizzontale andasse vista rispetto le sue componenti parallela al piano e una normale al piano, però pur vedendo le proprietà di due rette tagliate da una trasversale, come fate a dire che l'angolo che $F_O$ forma con la retta parallela al piano sia uguale a $theta$?
-Poi considerando la vostra osservazione che nella conservazione dell'energia meccanica avendo due incognite,o lo spostamento o la velocità che manca, io avrei cmq impostato così:
$0=mgh-LF_o$ sarebbe corretto, considerando che il lavoro svolto da una forza è l'opposto della sua energia potenziale è corretto?
-Infine se la velocità deve essere costante, il corpo doveva essere già in movimento, perchè se partisse da 0 e assumesse una velocità costante non sarebbe comunque un moto accelerato?
-Poi considerando la vostra osservazione che nella conservazione dell'energia meccanica avendo due incognite,o lo spostamento o la velocità che manca, io avrei cmq impostato così:
$0=mgh-LF_o$ sarebbe corretto, considerando che il lavoro svolto da una forza è l'opposto della sua energia potenziale è corretto?
-Infine se la velocità deve essere costante, il corpo doveva essere già in movimento, perchè se partisse da 0 e assumesse una velocità costante non sarebbe comunque un moto accelerato?
Angoli alterni interni di due rette tagliate da una trasversale sono congruenti.
La trasversale è il piano inclinato, le parallele sono il piano orizzontale e la direzione della forza ...
La trasversale è il piano inclinato, le parallele sono il piano orizzontale e la direzione della forza ...
"75america":
-Poi considerando la vostra osservazione che nella conservazione dell'energia meccanica avendo due incognite,o lo spostamento o la velocità che manca, io avrei cmq impostato così:
$0=mgh-LF_o$ sarebbe corretto, considerando che il lavoro svolto da una forza è l'opposto della sua energia potenziale è corretto?
No, non e' corretto. I principi sono 2 da ricordare come il vangelo
(1) In assenza di forze dissipative si conserva la somma di U + $E_k$. Non e' il tuo caso, perche c'e' attrito.
(2) Il lavoro di tutte le forze applicate (incluse le forze dissipative e' uguale alla variazione di $E_k$.
Questo e' il tuo caso. in questo caso la variazione di $E_k$
"75america":
-Infine se la velocità deve essere costante, il corpo doveva essere già in movimento, perchè se partisse da 0 e assumesse una velocità costante non sarebbe comunque un moto accelerato?
Infatti. Se il corpo e' fermo, la $F_0$ lo mantiene fermo (aumenta l'attrito). Se il corpo si fosse mosso con velocita v, la forza non varierebbe quella velocita' INDIPENDENTEMENTE DA v. Quindi non sei in grado di sapere qual e' lo spostamento in un qualsiasi lasso di tempo, ergo non puoi calcolare il lavoro fatto.
"professorkappa":
Infatti. Se il corpo e' fermo, la $F_0$ lo mantiene fermo (aumenta l'attrito). Se il corpo si fosse mosso con velocita v, la forza non varierebbe quella velocita' INDIPENDENTEMENTE DA v. Quindi non sei in grado di sapere qual e' lo spostamento in un qualsiasi lasso di tempo, ergo non puoi calcolare il lavoro fatto.
Professore nn riesco a capire:
1-allora se il corpo è fermo, la $F_0$ lo mantiene fermo,perchè noi abbiamo imposto che il corpo si muova con velocità costante, cioè in questo caso nulla,oppure se si muoveva già con velocità v, questa doveva rimanere tale nel tempo, giusto?
2-Il fatto di non poter sapere qual è lo spostamento in un qualsiasi lasso di tempo è dovuto semplicemente al fatto che non non conosciamo nemmeno un valore di velocità (se 0 o >0), quindi non possiamo conoscere il lavoro fatto.
Poi ha detto che in questo problema è valido il Teorema dell'Energia Cinetica,l'avevo capito anch'io:
$L_(Tot)=\DeltaK$
$LF_0cos30°-LF_(ad)$ (sec.membro =0, perchè la velocità è costante)
$F_0cos30°*s-ud(mgcostheta+F0sentheta)=0$ ,volevo sapere se come avevo scritto fosse valido, pur sapendo che il $LF_(ad)=-F_d*\DeltaS$
Poi
"professorkappa":, se il corpo si fosse mosso con velocità v, la Forza avrebbe un'intensità per cui la velocità rimanga costante, quindi il suo modulo a un certo punto si ferma per far proseguire il corpo a vel costante,spero che intendiamo la stessa cosa
Se il corpo si fosse mosso con velocita v, la forza non varierebbe quella velocita' INDIPENDENTEMENTE DA v
"75america":
Professore nn riesco a capire:
1-allora se il corpo è fermo, la $F_0$ lo mantiene fermo,perchè noi abbiamo imposto che il corpo si muova con velocità costante, cioè in questo caso nulla,oppure se si muoveva già con velocità v, questa doveva rimanere tale nel tempo, giusto?
2-Il fatto di non poter sapere qual è lo spostamento in un qualsiasi lasso di tempo è dovuto semplicemente al fatto che non non conosciamo nemmeno un valore di velocità (se 0 o >0), quindi non possiamo conoscere il lavoro fatto.
Risposta alla domanda (1) e (2) - Si, giusto.
"75america":
Poi ha detto che in questo problema è valido il Teorema dell'Energia Cinetica,l'avevo capito anch'io:
$L_(Tot)=\DeltaK$
$LF_0cos30°-LF_(ad)$ (sec.membro =0, perchè la velocità è costante)
$F_0cos30°*s-ud(mgcostheta+F0sentheta)=0$ ,volevo sapere se come avevo scritto fosse valido, pur sapendo che il $LF_(ad)=-F_d*\DeltaS$
Qui sbagli, (a) perche anche la componente della forza peso fa lavoro, quindi devi metterci dentro il termine
\( -mgsin\vartheta \) e (b) per lo spostamento una volta usi s e una volta d. Se correggi tenendo conto di a e b, ti rona esattamente il risultato gia' trovato in un post precedente.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo