Corpo spinto su pavimento scabro

[75america]

Un ragazzo tira un blocco di massa 10kg su un pavimento scabro (coeff. attrito statico us=0.3 e dinamico ud=0.2). Se il ragazzo applica una forza formante un angolo di 40° con l'orizzontale, calcolare la massima forza in modulo da applicare senza che il blocco si muova. Se il ragazzo raddoppia la forza con cui tira, calcolare l'accelerazione del blocco. Calcolare il lavoro fatto dal ragazzo dopo 1 min.



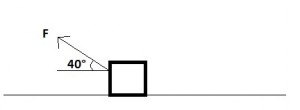
Allora qui il mio dubbio è di base, io ho usato la componente orizzontale della forza, quidi $F_x$ e usando solo questa nella condizione per l'equilibrio statico, quindi $F_x<=usN$, ma il problema chiede il modulo della forza, quindi vuole che usi anche la componente verticale, ma anche la componente verticale subisce la forza d'attrito?
Non ho capito se devo usare entrambe le componenti al fine del calcolo.

[axpgn]

Affinché il blocco non si muova la forza orizzontale applicata dal ragazzo deve essere inferiore alla massima forza esercitabile dall'attrito statico, quindi avremo

$F_x<=F_(s_(max))=mu_sN=mu_s(mg-F_y)$

$F(cos40°+mu_ssen40°)<=mu_smg$

$F<=(mu_smg)/(cos(40°)+mu_ssen(40°))$


Cordialmente, Alex