Carica e scarica di un condensatore
Ecco i grafici che trovo in giro
(anche sul libro di testo che sto usando sono così)
Carica di un condensatore
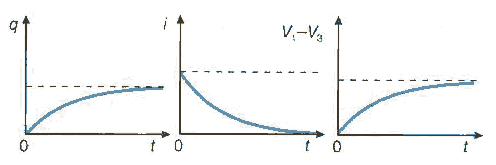
Scarica di un condensatore
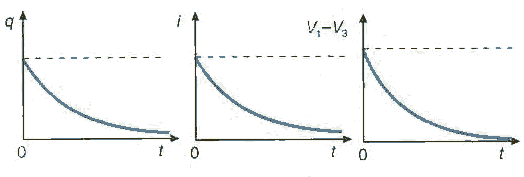
Perché il grafico dell'intensità di corrente è uguale sia nel caso della scarica che nel caso della carica?
Anche perché $i={dQ}/{dt}$ e se vado a vedere la pendenza della curva $q(t)$ ho che è negativa, quindi $i$ non dovrebbe essere a valori negativi?
E poi mi sembra di aver capito che quando il condensatore si scarica il verso della corrente è opposto al verso della carica, giusto?
(anche sul libro di testo che sto usando sono così)
Carica di un condensatore
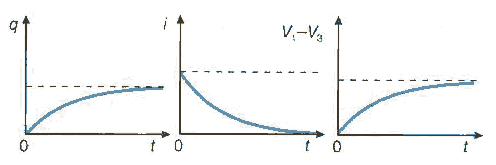
Scarica di un condensatore
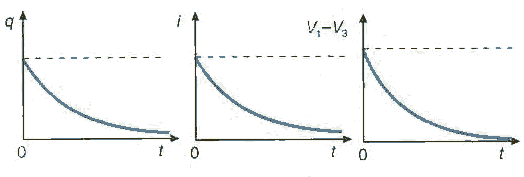
Perché il grafico dell'intensità di corrente è uguale sia nel caso della scarica che nel caso della carica?
Anche perché $i={dQ}/{dt}$ e se vado a vedere la pendenza della curva $q(t)$ ho che è negativa, quindi $i$ non dovrebbe essere a valori negativi?
E poi mi sembra di aver capito che quando il condensatore si scarica il verso della corrente è opposto al verso della carica, giusto?
Risposte
Si, hai perfettamente ragione. Direi che danno per scontato che uno capisca il verso della corrente.
Vedilo come il modulo della corrente, ...
Vedilo come il modulo della corrente, ...
Il fatto è che per convenzione:
1) la corrente ha il verso che va dal potenziale maggiore a quello minore;
2) l'intensità di corrente in una sezione di un conduttore è definita come la derivata temporale della carica elettrica che si trova a valle (rispetto al verso della corrente stessa) della sezione stessa.
Nel caso di un generatore che carica il condensatore, la corrente ha il verso che va dal morsetto positivo del generatore verso quello negativo, andando così a caricare positivamente l'armatura del condensatore a contatto col morsetto positivo. In tal caso, la carica che si trova a valle dei qualsiasi punto del ramo di circuito connesso all'elettrodo positivo del generatore è $+Q(t)$ e dunque la corrente è $i(t)=(dQ)/(dt)$.
Nel caso di scarica di un condensatore, questo si comporta istantaneamente come un generatore, la corrente ha il verso che va dall'armatura positiva a quella negativa, la carica a valle di qualsiasi punto è quindi quella, $-Q(t)$, dell'armatura caricata negativamente e in questo caso si ha quindi: $i(t)=-(dQ)/(dt)$.
Se provi a farti un disegno del circuito (cosa che in questo momento non riesco a fare) forse la cosa ti risulterà più comprensibile.
1) la corrente ha il verso che va dal potenziale maggiore a quello minore;
2) l'intensità di corrente in una sezione di un conduttore è definita come la derivata temporale della carica elettrica che si trova a valle (rispetto al verso della corrente stessa) della sezione stessa.
Nel caso di un generatore che carica il condensatore, la corrente ha il verso che va dal morsetto positivo del generatore verso quello negativo, andando così a caricare positivamente l'armatura del condensatore a contatto col morsetto positivo. In tal caso, la carica che si trova a valle dei qualsiasi punto del ramo di circuito connesso all'elettrodo positivo del generatore è $+Q(t)$ e dunque la corrente è $i(t)=(dQ)/(dt)$.
Nel caso di scarica di un condensatore, questo si comporta istantaneamente come un generatore, la corrente ha il verso che va dall'armatura positiva a quella negativa, la carica a valle di qualsiasi punto è quindi quella, $-Q(t)$, dell'armatura caricata negativamente e in questo caso si ha quindi: $i(t)=-(dQ)/(dt)$.
Se provi a farti un disegno del circuito (cosa che in questo momento non riesco a fare) forse la cosa ti risulterà più comprensibile.
Grazie ad entrambi per le risposte 
Vediamo se ho capito , quando il condensatore si carica io calcolo la d.d.p. percorrendo il circuito nel verso della corrente, diciamo orario. Quando invece si sta scaricando cambio il verso e assumo positivo quello antiorario, e calcolo la d.d.p. in senso antiorario.
Solo che avendo assunto $i$ positiva ho che la carica sull'armatura diminuisce nel tempo.
$i$ è positiva per il senso scelto mentre ${dq}/{dt}$ è negativa quindi $i=-dq/dt$, l'importante è che una sia positiva e l'altra negativa, giusto?
Quindi tornando al grafico o lo disegno nell'altro modo, cioè con la corrente negativa, oppure assumo che la corrente è presa in modulo .
"Palliit":
Il fatto è che per convenzione:
1) la corrente ha il verso che va dal potenziale maggiore a quello minore;
2) l'intensità di corrente in una sezione di un conduttore è definita come la derivata temporale della carica elettrica che si trova a valle (rispetto al verso della corrente stessa) della sezione stessa.
Nel caso di un generatore che carica il condensatore, la corrente ha il verso che va dal morsetto positivo del generatore verso quello negativo, andando così a caricare positivamente l'armatura del condensatore a contatto col morsetto positivo. In tal caso, la carica che si trova a valle dei qualsiasi punto del ramo di circuito connesso all'elettrodo positivo del generatore è $+Q(t)$ e dunque la corrente è $i(t)=(dQ)/(dt)$.
Nel caso di scarica di un condensatore, questo si comporta istantaneamente come un generatore, la corrente ha il verso che va dall'armatura positiva a quella negativa, la carica a valle di qualsiasi punto è quindi quella, $-Q(t)$, dell'armatura caricata negativamente e in questo caso si ha quindi: $i(t)=-(dQ)/(dt)$.
Se provi a farti un disegno del circuito (cosa che in questo momento non riesco a fare) forse la cosa ti risulterà più comprensibile.
Vediamo se ho capito , quando il condensatore si carica io calcolo la d.d.p. percorrendo il circuito nel verso della corrente, diciamo orario. Quando invece si sta scaricando cambio il verso e assumo positivo quello antiorario, e calcolo la d.d.p. in senso antiorario.
Solo che avendo assunto $i$ positiva ho che la carica sull'armatura diminuisce nel tempo.
$i$ è positiva per il senso scelto mentre ${dq}/{dt}$ è negativa quindi $i=-dq/dt$, l'importante è che una sia positiva e l'altra negativa, giusto?
Quindi tornando al grafico o lo disegno nell'altro modo, cioè con la corrente negativa, oppure assumo che la corrente è presa in modulo .


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo