Blocco-molla su piano inclinato
Questo problema è già stato risolto, ma nell'ultimo passaggio ho qualche problema
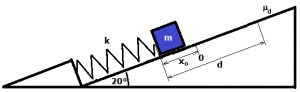
Un blocco di massa pari a m = 3,00 Kg è tenuto appoggiato contro una molla di costante elastica k = 25,00 N / cm comprimendo la molla di x0 = 3,00 cm dalla sua posizione di riposo.
Quando il blocco è rilasciato, la molla spinge il blocco verso l’alto lungo una superficie ruvida inclinata di un angolo di α = 20°.
Il coefficiente di attrito dinamico tra il blocco e la superficie è μd = 0,100.
Si determini la distanza d di quanto scivolerà il blocco sul piano inclinato prima che si fermi.
Allora:
L'nergia potenziale elastica $U_k$ accumulata dala molla:
$U_K=25N/cm=2500N/m $
$x_0=3cm=0.03m$
Calcolo COMP. Tang. e Normale al P.Inclinato della Forza Peso
$F_T=mgsentheta=3*9.8*0.34=10N$
$F_N=mgcostheta=29.4*0.93=27.34N$
Forza di Attrito Dinamico:
$F_d=u_dN=umgcostheta=2.76N$
Dato che sia la Forza d'attrito che la Componente della Forza Peso parallela al Piano Inclinato, si oppongono al moto del blocco
$F=F_d+F_T=2.76+10=12.76N$
Adesso per calcolarsi la distanza d percorsa dal blocco prima di fermarsi dicono che U_K si trasformi in lavoro fatto contro queste due forze , ma come facciamo a paragonare Energia Potenziale Elastica=Forza Peso+F.Attrito(considerando per giunta la Forza d'attrito non è conservativa),mah.
Un blocco di massa pari a m = 3,00 Kg è tenuto appoggiato contro una molla di costante elastica k = 25,00 N / cm comprimendo la molla di x0 = 3,00 cm dalla sua posizione di riposo.
Quando il blocco è rilasciato, la molla spinge il blocco verso l’alto lungo una superficie ruvida inclinata di un angolo di α = 20°.
Il coefficiente di attrito dinamico tra il blocco e la superficie è μd = 0,100.
Si determini la distanza d di quanto scivolerà il blocco sul piano inclinato prima che si fermi.

Allora:
L'nergia potenziale elastica $U_k$ accumulata dala molla:
$U_K=25N/cm=2500N/m $
$x_0=3cm=0.03m$
Calcolo COMP. Tang. e Normale al P.Inclinato della Forza Peso
$F_T=mgsentheta=3*9.8*0.34=10N$
$F_N=mgcostheta=29.4*0.93=27.34N$
Forza di Attrito Dinamico:
$F_d=u_dN=umgcostheta=2.76N$
Dato che sia la Forza d'attrito che la Componente della Forza Peso parallela al Piano Inclinato, si oppongono al moto del blocco
$F=F_d+F_T=2.76+10=12.76N$
Adesso per calcolarsi la distanza d percorsa dal blocco prima di fermarsi dicono che U_K si trasformi in lavoro fatto contro queste due forze , ma come facciamo a paragonare Energia Potenziale Elastica=Forza Peso+F.Attrito(considerando per giunta la Forza d'attrito non è conservativa),mah.
Risposte
Prima di tutto, la forza $F$ deve avere la forza della molla.
Quindi l'ultima equazione va scritta come:
\( F = -12.76N + kx = m\ddot{x} \) (il segno meno tiene conto del fatto che attrito e forza peso sono discordi con il sistema di riferimento scelto
x = 0 quando la molla e' scarica.
Da qui puoi ricavare la velocita \( \dot{x} \) in x=0, cioe' quando il corpo abbaonda la molla.
Da quel punto in poi, le uniche forze agenti sono la forza peso e la resistenza del piano, quindi puoi calcolare l'accelerazione del corpo.
\( -12.76 = m\ddot{x} \)
Avendo l'accelerazione, sei in grado per integrazione di calcolare velocita' e spazio (tenendo conto delle condizioni al contorno, cioe' posizione e velocita del corpo all'istante t=0).
Risalire allo spazio percorso risulta banale, basta annullare la \( \dot{x}(t) \) , ricavando un tempo di frenata $t_f$ che sostituito in x(t) ti da $x_f$ spazio di frenata.
Usando le energie, tutta la pappardella sopra si semplifica enormemente!
Quindi l'ultima equazione va scritta come:
\( F = -12.76N + kx = m\ddot{x} \) (il segno meno tiene conto del fatto che attrito e forza peso sono discordi con il sistema di riferimento scelto
x = 0 quando la molla e' scarica.
Da qui puoi ricavare la velocita \( \dot{x} \) in x=0, cioe' quando il corpo abbaonda la molla.
Da quel punto in poi, le uniche forze agenti sono la forza peso e la resistenza del piano, quindi puoi calcolare l'accelerazione del corpo.
\( -12.76 = m\ddot{x} \)
Avendo l'accelerazione, sei in grado per integrazione di calcolare velocita' e spazio (tenendo conto delle condizioni al contorno, cioe' posizione e velocita del corpo all'istante t=0).
Risalire allo spazio percorso risulta banale, basta annullare la \( \dot{x}(t) \) , ricavando un tempo di frenata $t_f$ che sostituito in x(t) ti da $x_f$ spazio di frenata.
Usando le energie, tutta la pappardella sopra si semplifica enormemente!
Ciao America, ho visto il PM ma per qualche motivo non riesco a rispondere.
Certamente ti posso dare una mano, siamo tutti qui per questo, ma a volte scrivere diventa complicato. Vediamo se mi riesce passaggio per passaggio.
Innanzitutto, il sistema di riferimento e' tale che l'origine e' nel punto in cui la molla e' rilassata e diretto verso l'alto, parallelamente al piano. Con questo riferimento, la posizione del blocco $x(0) = -x_0$. Nota il segno negativo!
in un generico punto $x$ compreso tra $x=-x_0$ e $x=0$ sul corpo agiscono
La forza della molla (positiva, perche tende a spingere il corpo nel senso delle x crescenti) $F_m = kx$
La componente forza peso (negativa, perche diretta nel verso dell x negative): \( F_p=-mgsin\vartheta \)
E la forza di attrito (negativa, i.c.s): \( F_a=-\mu mgcos\vartheta \)
Pertanto, basta sommare le forze sopra per avere che:
\( kx-mgsin\vartheta -\mu mgcos\vartheta =kx-mg(sin\vartheta -\mu cos\vartheta )=m\ddot{x} \)
Riarrangiando i termini:
\( m\ddot{x-}kx+mg(sin\vartheta -\mu cos\vartheta )=0 \)
RIPETO: valida solo tra $x=-x_0$ e $x=0$
Equazione differenziale che lascio risolvere a te prima di continuare.
Certamente ti posso dare una mano, siamo tutti qui per questo, ma a volte scrivere diventa complicato. Vediamo se mi riesce passaggio per passaggio.
Innanzitutto, il sistema di riferimento e' tale che l'origine e' nel punto in cui la molla e' rilassata e diretto verso l'alto, parallelamente al piano. Con questo riferimento, la posizione del blocco $x(0) = -x_0$. Nota il segno negativo!
in un generico punto $x$ compreso tra $x=-x_0$ e $x=0$ sul corpo agiscono
La forza della molla (positiva, perche tende a spingere il corpo nel senso delle x crescenti) $F_m = kx$
La componente forza peso (negativa, perche diretta nel verso dell x negative): \( F_p=-mgsin\vartheta \)
E la forza di attrito (negativa, i.c.s): \( F_a=-\mu mgcos\vartheta \)
Pertanto, basta sommare le forze sopra per avere che:
\( kx-mgsin\vartheta -\mu mgcos\vartheta =kx-mg(sin\vartheta -\mu cos\vartheta )=m\ddot{x} \)
Riarrangiando i termini:
\( m\ddot{x-}kx+mg(sin\vartheta -\mu cos\vartheta )=0 \)
RIPETO: valida solo tra $x=-x_0$ e $x=0$
Equazione differenziale che lascio risolvere a te prima di continuare.
professore allora con tutta la buona volontà non la capisco,
allora quell' $mx:$ che cosa rapprensenta?
poi in due parole al momento che la molla rilascia, spingendo il blocco verso l'alto come devo impostare le energie per conoscere la distanza percorsa dal blocco?
allora quell' $mx:$ che cosa rapprensenta?
poi in due parole al momento che la molla rilascia, spingendo il blocco verso l'alto come devo impostare le energie per conoscere la distanza percorsa dal blocco?
x e' la posizione del blocco
\( \ddot{x} \) e' la derivata seconda rispetto al tempo della posizione, cioe' e' l'accelerazione del blocco.
\( m\ddot{x} \) e' di conseguenza la risultante di tutte le forze agenti sul blocco.
Dov'e' il problema?
Questo problema lo puoi risolvere in 2 modi: con le equazioni cardinali (F=ma) o con i bilanci energetici.
Io ti sto spiegando come risolverlo con le equazioni cardinali, che e' il metodo che hai scelto tu all'inizio dell'esercizio, salvo poi tirare in ballo i bilanci energetici.
Sei in grado di calcolare x(t) risolvendo quel'equazione cardinale?
\( \ddot{x} \) e' la derivata seconda rispetto al tempo della posizione, cioe' e' l'accelerazione del blocco.
\( m\ddot{x} \) e' di conseguenza la risultante di tutte le forze agenti sul blocco.
Dov'e' il problema?
Questo problema lo puoi risolvere in 2 modi: con le equazioni cardinali (F=ma) o con i bilanci energetici.
Io ti sto spiegando come risolverlo con le equazioni cardinali, che e' il metodo che hai scelto tu all'inizio dell'esercizio, salvo poi tirare in ballo i bilanci energetici.
Sei in grado di calcolare x(t) risolvendo quel'equazione cardinale?
prof allora ho provato(nn avevo capito che quell'$x:$ fosse $x"$ dell'equ. diffirenziale di sec. gradio ordinaria)
3x"-2500x+29.4(0.34-0.0939)=0
allora credo si andrà con soluzioni con $e^(....)$,decisamente troppo complicato, se volessimo fare invece come lei suggerisce con i bilanci energetici come si potrebbe fare?
grazie sempre
3x"-2500x+29.4(0.34-0.0939)=0
allora credo si andrà con soluzioni con $e^(....)$,decisamente troppo complicato, se volessimo fare invece come lei suggerisce con i bilanci energetici come si potrebbe fare?
grazie sempre
Con il prinicipio di NON conservazione dell'energia meccanica.
Se non ci fosse attrito, prendendo come istanto 0 la molla compressa, e come istante 1 il blocco fermo, si dovrebbe verificare che:
\( E_{ko}+U_0=E_{k1}+U_1 \)
Cioe' la somma di Energia cinetica e Energia potenziale nella posizione 0 deve eguagliare la somma Energia cinetica e Energia potenziale nella posizione 1.
Calcoliamo questi termini.
$E_{k0}$ = 0 Il corpo e' fermo.
L'energia potenziale ha due componenti: l'energia potenziale dovuta al campo gravitazionale e l'energia potenziale della molla. Se sceglo come riferimento per l'energia potenziale gravitazionale il punto a molla compressa, mi rimane solo l'energia potenziale della molla, qundi:
\( U_0=\frac{1}{2}kx^2_0 \)
Nel punto di arrivo, dopo che il corpo ha percorso un tratto d (misurato dall'origine che e' nel punto a molla scarica) vale la relazione analoga.
$E_{k1}$ = 0 Il corpo e' fermo.
L'energia potenziale e' solo dovuta al campo gravitazionale. E siccome il corpo si trova ad altezza \( (d+x_0)sin\alpha \) rispetto allo 0 potenziale, la sua energia potenziale sara'
\( U_1 = mg(d+x_0)sin\alpha \)
Eguagliando membro a membro ottieni
\( mg(d+x_0)sin\alpha = \frac{1}{2}kx^2_0 \)
Cioe' l'energia totale in 1 (membro a sinistra), eguaglia l'energia totale in 0 (membro a destra).
Questo varrebbe se non ci fosse attrito.
Ma siccome l'attrito c'e', nel passare da 0 a 1 il corpo deve lasciare un po di soldini al tavolo del black jack dell'energia. Ne consegue che l'energia in 1 sara uguale a quella in 0 meno l'energia dissipata per attrito.
L'energia dissipata per attrito (in modulo) e' data dal lavoro della forza d'attrito lungo il tratto $(x_0+d)$, cioe:
\( E=F_a(x_0+d) \)
Quindi
\( mg(d+x_0)sin\alpha = \frac{1}{2}kx^2_0 - \mu \cdot mgcos\vartheta(x_0+d) \) \) , avendo tenuto conto che
\( F_a=\mu\cdot mgcos\vartheta \).
dall'ultima equazione risulta facile trovare d.
Spero sia sufficiente chiaro.
saluti
PK
Se non ci fosse attrito, prendendo come istanto 0 la molla compressa, e come istante 1 il blocco fermo, si dovrebbe verificare che:
\( E_{ko}+U_0=E_{k1}+U_1 \)
Cioe' la somma di Energia cinetica e Energia potenziale nella posizione 0 deve eguagliare la somma Energia cinetica e Energia potenziale nella posizione 1.
Calcoliamo questi termini.
$E_{k0}$ = 0 Il corpo e' fermo.
L'energia potenziale ha due componenti: l'energia potenziale dovuta al campo gravitazionale e l'energia potenziale della molla. Se sceglo come riferimento per l'energia potenziale gravitazionale il punto a molla compressa, mi rimane solo l'energia potenziale della molla, qundi:
\( U_0=\frac{1}{2}kx^2_0 \)
Nel punto di arrivo, dopo che il corpo ha percorso un tratto d (misurato dall'origine che e' nel punto a molla scarica) vale la relazione analoga.
$E_{k1}$ = 0 Il corpo e' fermo.
L'energia potenziale e' solo dovuta al campo gravitazionale. E siccome il corpo si trova ad altezza \( (d+x_0)sin\alpha \) rispetto allo 0 potenziale, la sua energia potenziale sara'
\( U_1 = mg(d+x_0)sin\alpha \)
Eguagliando membro a membro ottieni
\( mg(d+x_0)sin\alpha = \frac{1}{2}kx^2_0 \)
Cioe' l'energia totale in 1 (membro a sinistra), eguaglia l'energia totale in 0 (membro a destra).
Questo varrebbe se non ci fosse attrito.
Ma siccome l'attrito c'e', nel passare da 0 a 1 il corpo deve lasciare un po di soldini al tavolo del black jack dell'energia. Ne consegue che l'energia in 1 sara uguale a quella in 0 meno l'energia dissipata per attrito.
L'energia dissipata per attrito (in modulo) e' data dal lavoro della forza d'attrito lungo il tratto $(x_0+d)$, cioe:
\( E=F_a(x_0+d) \)
Quindi
\( mg(d+x_0)sin\alpha = \frac{1}{2}kx^2_0 - \mu \cdot mgcos\vartheta(x_0+d) \) \) , avendo tenuto conto che
\( F_a=\mu\cdot mgcos\vartheta \).
dall'ultima equazione risulta facile trovare d.
Spero sia sufficiente chiaro.
saluti
PK


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo