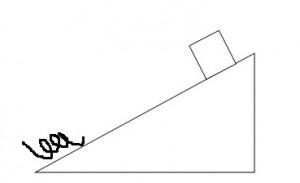
Blocco lasciato cadere su piano inclinato che tocca molla
Una molla sottoposta ad una forza di 100N si comprime di 20 cm. Un blocco di massa 3kg è lasciato da fermo dalla cima di un piano inclinato di 30° ad una distanza di 1.5m dalla molla non compressa. Calcolare la massima compressione della molla e la velocità del blocco nell'istante in cui tocca la molla.
Allora in questo problema riesco a calcolarmi solo la velocità d'impatto con la molla.
Diagramma forze:
$mgsentheta=ma==>a=4.9m/s^2$
La molla essendo compressa di $20cm=0.2m$, quindi il corpo si trova a $1.7m$ di distanza dalla molla
Quindi toccherà la molla con questa velocità:
$v^2=v_0^2+2a(x-x_0)$
$v^2=9.8*1.7==>v=sqrt(16.66)=4.08m/s$

Allora in questo problema riesco a calcolarmi solo la velocità d'impatto con la molla.
Diagramma forze:
$mgsentheta=ma==>a=4.9m/s^2$
La molla essendo compressa di $20cm=0.2m$, quindi il corpo si trova a $1.7m$ di distanza dalla molla
Quindi toccherà la molla con questa velocità:
$v^2=v_0^2+2a(x-x_0)$
$v^2=9.8*1.7==>v=sqrt(16.66)=4.08m/s$
Risposte
Leggi attentamente il testo.
La prima frase serve solo per dirti la costante $k$, non afferma che la molla è già compressa.
La velocità la puoi trovare con la conservazione dell'energia: in alto solo energia potenziale, in basso solo energia cinetica (ovviamente ipotizzando che la quota zero sia il punto di contatto con la molla).
Allo stesso modo calcoli la compressione della molla, è solo un filino più complicato perché al momento dell'impatto hai solo energia cinetica ma quando la molla è compressa avrai energia potenziale elastica ed energia potenziale gravitazionale.
Cordialmente, Alex
La prima frase serve solo per dirti la costante $k$, non afferma che la molla è già compressa.
La velocità la puoi trovare con la conservazione dell'energia: in alto solo energia potenziale, in basso solo energia cinetica (ovviamente ipotizzando che la quota zero sia il punto di contatto con la molla).
Allo stesso modo calcoli la compressione della molla, è solo un filino più complicato perché al momento dell'impatto hai solo energia cinetica ma quando la molla è compressa avrai energia potenziale elastica ed energia potenziale gravitazionale.
Cordialmente, Alex
Alex allora, ho iniziato:
$F_el=100N$
$F_el=-kx$, in uqesto caso prendendo la quota 0 il punto di contatto con la molla
$K=F_el/-x=100/0.2=500N/m$
Però poi mi devi spiegare l'utilità di prendere la quota 0 in quel punto, perchè non mi è chiara
se faccio la conser dell'energia meccanica $E_(p,A)=E_(K,B)$, io l'energia potenziale in A, dato che agisce solo la potenziale della forza peso lì serve la quota y, e io da dove le ricavo?
$F_el=100N$
$F_el=-kx$, in uqesto caso prendendo la quota 0 il punto di contatto con la molla
$K=F_el/-x=100/0.2=500N/m$
Però poi mi devi spiegare l'utilità di prendere la quota 0 in quel punto, perchè non mi è chiara
se faccio la conser dell'energia meccanica $E_(p,A)=E_(K,B)$, io l'energia potenziale in A, dato che agisce solo la potenziale della forza peso lì serve la quota y, e io da dove le ricavo?
Hai ricavato $k$ ed è ok.
L'utilità di avere quota zero all'imbocco della molla sta nel fatto che conosci la distanza tra molla e blocco (sul piano inclinato), quindi dato l'angolo conosci anche la quota del blocco che è $h=L*sin(30°)=0.75\ m$.
A sto punto ... prosegui tu per adesso ...
Cordialmente, Alex
P.S.:
Consiglio: quando parli di punti $A, B, ...$ facci sapere anche a noi dove sono (oltreché nella tua testa ... .
.
Nota: quando calcoli la costante elastica non ti serve nessuna quota! Tu sai che per comprimere la molla di $20\ cm$ occorre una forza di $100\ N$, quindi basta fare una divisione ...
L'utilità di avere quota zero all'imbocco della molla sta nel fatto che conosci la distanza tra molla e blocco (sul piano inclinato), quindi dato l'angolo conosci anche la quota del blocco che è $h=L*sin(30°)=0.75\ m$.
A sto punto ... prosegui tu per adesso ...

Cordialmente, Alex
P.S.:
Consiglio: quando parli di punti $A, B, ...$ facci sapere anche a noi dove sono (oltreché nella tua testa ...
 .
.Nota: quando calcoli la costante elastica non ti serve nessuna quota! Tu sai che per comprimere la molla di $20\ cm$ occorre una forza di $100\ N$, quindi basta fare una divisione ...
Allora ho provato a calcolarmi la misura della compressione all'impatto tra la massa e la molla
$F_B=ma =>$ $mgsentheta=ma$
$F_B=14,7N=500x=>x=0.03m$
Però ho paura di aver sbagliato e soprattutto di aver usato il metodo di calcolo sbagliato
La paura..
$F_B=ma =>$ $mgsentheta=ma$
$F_B=14,7N=500x=>x=0.03m$
Però ho paura di aver sbagliato e soprattutto di aver usato il metodo di calcolo sbagliato
La paura..
La paura, ma anche la mancanza di teoria, pero'.
Riguardati la parte relativa alla conservazione dell'energia meccanica. Non ha senso svolgere i problemi senza toeria. E' come mettere un tetto a una casa senza muri.
La soluzione te l'ha data axpgn
Riguardati la parte relativa alla conservazione dell'energia meccanica. Non ha senso svolgere i problemi senza toeria. E' come mettere un tetto a una casa senza muri.
La soluzione te l'ha data axpgn
Allora partendo dalla teoria:
Conserv. Energia Meccanica, (in presenza di forze conservative)
$K(A)+U(A)=K(B)+U(B)$
Energia Poten. Elastica-Energia Pot.Forza Peso=En.Cinet
$1/2kx^2-mgh=1/2mv_B^2$
considerando che $h=Lsen30°=1.5/2=0.75m$
-Con questa formula riuscirei a calcolarmi la massima compressione possibile della molla?
Perchè io la velocità d'impatto la conosco per mezzo di $v^2=v_0^2+2a(x-x_0)$ cioè 3.83 m/s
-Poi non è che l'energia pot della forza peso andava sommata e non sottratta a quella potenziale elastica?
Cioè io non capisco, prima agisce l'energia potenziale della forza peso, però al momento dell'impatto non dovrebbero agire entrambe quindi chi sono U(A) e (B)?
Conserv. Energia Meccanica, (in presenza di forze conservative)
$K(A)+U(A)=K(B)+U(B)$
Energia Poten. Elastica-Energia Pot.Forza Peso=En.Cinet
$1/2kx^2-mgh=1/2mv_B^2$
considerando che $h=Lsen30°=1.5/2=0.75m$
-Con questa formula riuscirei a calcolarmi la massima compressione possibile della molla?
Perchè io la velocità d'impatto la conosco per mezzo di $v^2=v_0^2+2a(x-x_0)$ cioè 3.83 m/s
-Poi non è che l'energia pot della forza peso andava sommata e non sottratta a quella potenziale elastica?
Cioè io non capisco, prima agisce l'energia potenziale della forza peso, però al momento dell'impatto non dovrebbero agire entrambe quindi chi sono U(A) e (B)?
Non proprio.
Stabilito k come hai fatto tu applichiamo il teorema di conservazione dell'energia.
Chiamiamo A la condizione iniziale quando il blocco e' a 1.5m dalla molla compressa.
Se il riferimento per il calcolo dell'energia potenziale e' (arbirtrariamente) l'estremita della molla, il Sistema che energia meccanica (intesa come $E_K$+U) avra' in quel punto?
Seconda posizione (B), che' quella che cerca il problema (massimia compressione). Che energia meccanica ha ora il sistema? (non cambiare il riferimento per l'energia potenziale, eh?
Terza posizione: (C): Istante in cui il punto impatta la molla. Che energia meccanica ha ora il sistema? (non cambiare il riferimento per l'energia potenziale, eh?
Se scrivi queste 3 equazioni correttamente hai le risposte al problema.
Vai, attacca a scrivere!
Ciao
PK
Stabilito k come hai fatto tu applichiamo il teorema di conservazione dell'energia.
Chiamiamo A la condizione iniziale quando il blocco e' a 1.5m dalla molla compressa.
Se il riferimento per il calcolo dell'energia potenziale e' (arbirtrariamente) l'estremita della molla, il Sistema che energia meccanica (intesa come $E_K$+U) avra' in quel punto?
Seconda posizione (B), che' quella che cerca il problema (massimia compressione). Che energia meccanica ha ora il sistema? (non cambiare il riferimento per l'energia potenziale, eh?

Terza posizione: (C): Istante in cui il punto impatta la molla. Che energia meccanica ha ora il sistema? (non cambiare il riferimento per l'energia potenziale, eh?

Se scrivi queste 3 equazioni correttamente hai le risposte al problema.
Vai, attacca a scrivere!
Ciao
PK


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo