Blocco lanciato su un piano inclinato

[angelox9]

Un blocco di massa m =1 kg viene lanciato su per un piano inclinato scabro (μ=0.2) con velocità v0=3 m/s.
Se l'angolo di inclinazione è α=30°, calcolare:
(a) la distanza s percorsa dal blocco lungo il piano;
(b) il tempo impiegato a percorrerla, nonché‚ il tempo complessivo di andata e ritorno;
(c) l'energia trasformata in calore lungo l'intero percorso.

Potete dirmi se i passaggi sono corretti?

Come calcolare il punto c?





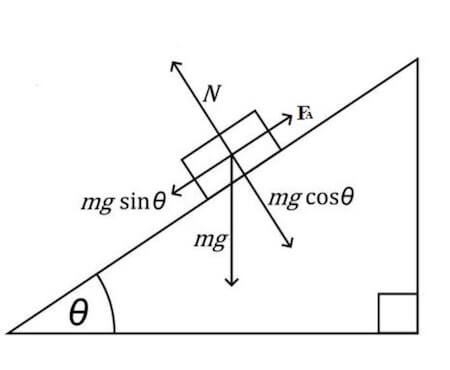
Disegno:


Dati:
$ m = 1 kg $

$ μ=0.2$

$ v_{0}=3 m/s $

$ α=30° $

a) Calcoliamo lo spazio percorso:

$ F_{\text{tot}} = vecF_{\text{att}}+vecN+vecP = mveca $

$ { ( F_{k} = μ_{k}N ),( F_{\text{attx}}+N_{x}+P_{x} = ma_{x} ),( F_{\text{atty}}+N_{y}+P_{y} = ma_{y} ):} $

$ { ( F_{k} = μ_{k}N ),( -F_{\text{attx}}-P_{x} = ma_{x} ),( N_{y}-P_{y} = 0 ):} $

$ { ( F_{k} = μ_{k}N ),( -F_{\text{attx}}-P sin \theta = ma_{x} ),( N_{y}-P cos \theta = 0 ):} $

$ { ( F_{k} = μ_{k}N ),( -F_{\text{k}} = ma +P sin \theta ),( N = P cos \theta ):} $

$ { ( F_{k} = μ_{k}N ),( -F_{\text{k}} = ma +mg sin \theta ),( N = mg cos \theta ):} $

$ { ( F_{k} = μ_{k}mg cos \theta ),( F_{\text{k}} = -m(a +g sin \theta) ),( N = mg cos \theta ):} $

Calcoliamo a:
$ -m(a + g sin \theta ) = μ_{k}mg cos \theta $
$ a + g sin \theta = -μ_{k}g cos \theta $
$ a = - g sin \theta -μ_{k}g cos \theta $
$ a = -g( sin \theta + μ_{k} cos \theta ) $

$ a = -g( sin \theta + μ_{k} cos \theta ) = -9.8(sin 30+0.2*cos 30) = -6.60 m/s^2$

$ v^2-v_{0}^2 = 2aS $

$ -v_{0}^2 = 2aS $

$ S = (-v_{0}^2)/(2a) = (-(3 m/s)^2)/(2*-6.60 m/s^2) = 0.68 m$

b)

Calcoliamo il tempo di salita:

$ v(t) = v_{0}+at = v_{0}-g( sin \theta + μ_{k} cos \theta )t $
$ v_{0}-g( sin \theta + μ_{k} cos \theta )t = 0 $
$ -g( sin \theta + μ_{k} cos \theta )t = - v_{0} $
$ t = v_{0}/(g( sin \theta + μ_{k} cos \theta )) = (3 m/s) / (9.8m/s^2+(sin 30 * 0.2 * cos 30)) = 0.4547 s = 0.455 s = 0.46 s $

Calcoliamo il tempo di discesa:
$ { ( F_{k} = μ_{k}mg cos \theta ),( N = mg cos \theta ), ( F_{\text{k}} -mg sin \theta = -ma ):} $
$ { ( F_{k} = μ_{k}mg cos \theta ),( N = mg cos \theta ), ( μ_{k}mg cos \theta -mg sin \theta = -ma ):} $

$ μ_{k}mg cos \theta -mg sin \theta = -ma $
$ - ma = μ_{k}mg cos \theta -mg sin \theta $
$ a = g (sin \theta -μ_{k} cos \theta) $


$ x(t) = x_{0}+v_{0}t+1/2at^2 $
$ 0 = 0,68m - 1/2at^2 $
$ - 0,68m = - 1/2at^2 $
$ 2 * 0,68m = at^2 $
$ t^2 = (2 * 0,68m)/a $
$ t = sqrt((2 * 0,68)/a) = sqrt((2 * 0,68m)/g (sin \theta -μ_{k} cos \theta)) = sqrt((2 * 0,68m)/((9.8 m/s^2) (sin 30 -0.2 cos 30))) = sqrt((1.36m)/(3.20 m/s^2)) = 0.65 s $

[Shackle]

L’energia che si trasforma in calore in tutto il tragitto è uguale al lavoro totale della forza di attrito, che è non conservativa.

[angelox9]

Dici cosi:

$ \DeltaE_{1} = E_{f}-E_{i} = U_{f}+K_{f}-(U_{i}+K_{i}) = mgh + 0 - 0 - 1/2 mv_{o}^2$
$ \DeltaE_{2} = E_{f}-E_{i} = U_{f}+K_{f}-(U_{i}+K_{i}) = 0 + 1/2 mv^2 - mgh - 0$
$ W_{\text{nc}}= \DeltaE_{t} = \DeltaE_{1}+\DeltaE_{2} = mgh - 1/2 mv_{o}^2 + 1/2 mv^2 - mgh = 1/2 mv^2 - 1/2 mv_{o}^2 = 1/2 m(v^2 - v_{o}^2)$

[Shackle]

Intendo l’applicazione del principio della fisica, in base al quale il lavoro delle forze non conservative è uguale alla variazione di energia meccanica del sistema. Se i passaggi sono quelli giusti, è quello che hai scritto ( non li ho verificati).

Però toglimi un dubbio. Se poni l’energia potenziale finale uguale a zero : $U_f = 0 $ , vuol dire che il corpo alla fine si ritrova a livello zero, da dove era partito con velocità $v_0$ . E come mai lo spostamento da te determinato in discesa non è uguale, in modulo, allo spostamento in salita?
Non puoi trovare il lavoro della forza d’attrito nei due tragitti come prodotto scalare $vecF*vecs $ ?