Asta orizzontale sorregge carico

[75america]

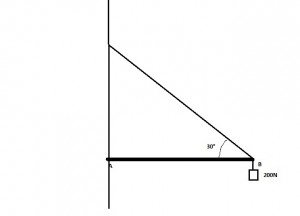
Un'asta orizzontale omogenea AB di lunghezza l=2m e massa M=1kg sorregge un carico di 200N. L'asta è collegata alla parete da un perno in A. Determinare la tensione del cavo e la reazione del perno.

[75america]

Allora provato a risolverlo, ma facendo i calcoli mi trovo con la resistenza del Perno $R_(py)$ non mi viene uguale a 0, come io penso che invece debba essere

$mg+T+Rp+Mg=0$
da cui proiettando sugli assi X, orizzontale parallelo e concorde con $AB$, e Y verticale verso l'alto, si ha:
$R_(px)-Tcostheta=0$
$R_(py)-mg-Mg+Tsentheta=0$

$M=0$ 2°Eq. cardinale statica: assunto polo P
$T_b-mgL-Mg(L/2)=0$

Ma il braccio $b$ della tensione è l'altezza relativa all'ipotenusa del triangolo
$b=Lsentheta$
Sostituendo otteniamo:
$TLsentheta-mgL-Mg(L/2)=0$
Semplificando L, ottengo:
$Tsentheta-mg-(Mg)/2=0$
$T=(mg+(Mg)/2)/(sentheta)$

Dalle proiezioni:
$R_(px)=(mg+(Mg)/2) cotg\theta$
$R_(py)=(Mg)/2$

secondo me,però $R_(py)$ dovrebbe essere $=0$, perchè la resistenza del perno non forma angoli, quindi dovrebbe esserci solo lungo l'asse $x$

[Rob995]

Ahah figurati assolutamente non per critica però gli esercizi di isostatica ti stanno proprio antipatici eh 75america? poi figurati ne capisco quanto te, penso tu sia al primo anno di università come me. Detto questo mi sembra tu abbia fatto tutto giusto tranne la considerazione che un vincolo non può esercitare forze. Scusa se tu prendi un bastone in mano, tipo della scopa, e ci appendi all'estremo una bottiglia d'acqua non devi esercitare una forza, e pure abbastanza intensa, per sorreggere il tutto? A maggior ragione qui la tensione ha una componente orizzontale che come giustamente hai scritto deve essere controbilanciata da un'altra componente orizzontale, quindi già da questo sei sicuro che il vincolo una corza orizzontale la esercita. In più sappi che una corda, che tipo ho letto ieri si chiama vincolo unilaterale, può esercitare solo forze lungo la direzione in cui è tesa. Una sbarra o qualunque altra cosa, può avere reazioni anche fuori dalla direzione in cui è posta. Spero di aver chiarito il dubbio..

[axpgn]

"75america":... ma facendo i calcoli mi trovo con la resistenza del Perno $R_(py)$ non mi viene uguale a 0, come io penso che invece debba essere ...
secondo me,però $R_(py)$ dovrebbe essere $=0$, perchè la resistenza del perno non forma angoli, quindi dovrebbe esserci solo lungo l'asse $x$

Ma perché? Se rileggi l'esempio che ti ho fatto ieri per un esercizio simile forse ti convincerai ... oppure mettiamo che la fune sia verticale (questa sì può avere solo la componente verticale ...), se togli il muro che fine fa l'estremo A? Mentre l'altro estremo B rimane dov'è grazie alla fune, l'estremo A cade giù ... e se prima stava su una qualche forza verticale il perno la esercitava

[75america]

axpgn sarà che so di coccio, ma allora il perno (cioè sto pezzo di muro) esercita una resistenza nel tenere il punto A (cioè la sbarra) attaccata nel punto A, te mi devi dire perchè deve compiere una resistenza anche lungo la verticale per poterla mantere in orizzontale?

Poi io se dico che per me non devono esserci componenti è perchè (così ho capito, sicuramente in modo sbgliato) che i vettori si scompongono in componenti però deve esserci l'angolo altrimenti o sono solo presenti su x o solo su y

[axpgn]

Nel mio esempio probabilmente (ma andrebbe calcolato caso per caso) il perno non avrà componente verticale, mentre in questo caso (quasi) sicuramente sì dato che la fune è obliqua.
Anche oggi ti stai fissando su cose che non esistono ... non confondere l'angolo formato dall'asta e dal muro con l'angolo che forma la reazione del perno con l'asta: tu NON VEDI in quale direzione agisce la forza di reazione; solo dopo averla calcolata saprai dove va ... detto in altro modo, oggi come ieri, continui a confondere le direzioni delle forze con linee geometriche, ma questo è vero solo in alcuni casi, come le funi per esempio, in generale non è detto ...
Detto in altro modo ancora: tu puoi farti tutte le idee che vuoi (ed anche giusto che sia così, anzi fai bene a farlo), però poi parti da quello che conosci, cerca di trovare le soluzioni e alla fine, criticamente, discuti (con te stesso ) se quello che hai trovato è coerente con quello che sai ed hai imparato; non porre però per dato quello che tu pensi sia giusto, ma mettilo in discussione con quello che trovi.

[75america]

axpgn ho ragionato così perchè nei diagrammi delle forze nei piani inclinati ragionavo così e trovandomi con gli esercizi, pernso di aver ragionato bene, ma a quanto vedo, per queste aste non è valido il mio ragionamento, allora ti pongo l'ennesima domanda, in quali casi è valido il mio ragionamento, molto ragionato sulla figura??
grazie per tutte le info, dico davvero

[75america]

allora ho continuato i calcoli, ma credo che non siano corretti perchè il carico appeso è 200N,potete controllare voi?
$R_(py)=4,9N$
$R_(px)=(200*9.8+4.9)=1964.9N$

Tensione T:
$T=(mg+(Mg)/2)/(sentheta)$
$T=(200*9.8+4.9)/(sen30°)$=1964.9/0.5=3929,8N$

ho paura che non abbia considerato la massa (200N in kg, anche se ho moltiplicato per 9.8...sto impazzendo)

[axpgn]

"75america":axpgn ho ragionato così perchè nei diagrammi delle forze nei piani inclinati ragionavo così ...

Con i piani inclinati di solito è più semplice, le forze sono tutte "visibili" di solito ...

Qui è lo stesso ... se appoggi un'asta su di un piano inclinato tu scomponi l'eventuale forza che questa esercita sul piano nelle due componenti (parallela al piano e normale al piano). Anche in questo caso puoi fare la stessa cosa, ma c'è una differenza che non cogli: mentre qui è sempre il perno che reagisce ad entrambe le componenti, sul piano inclinato la forza normale reagisce SOLO alla componente normale, mentre alla componente parallela reagisce eventualmente l'attrito, o una fune, od anche niente e l'asta ... scivola.
Confondi la forza normale di reazione del piano (che, lo dice la parola, è sempre normale al piano) con la reazione del perno che invece reagisce ad entrambe le componenti. Più chiaro così?

L'equazione relativa ai momenti (usando il perno come asse) è la seguente:

$(Mgl)/2+C*l-T*l*sin(alpha)=0$ e sostituendo abbiamo $(1*9.8*2)/2+200*2-T*2/2=0$.
Come vedi hai una sola incognita e risolvendo trovi che $9.8+400=T$ ed infine $T=409.8 N$.
Ti torna? Poi prosegui ...
Cordialmente, Alex

[75america]

axpgn giusto per compliecarti la vita, pensavo che l'asta rispetto al muro potesse muoversi solamente in orizzontale e quindi esserci solo l'asse x, si mi è più chiaro, ma trovare una spiegazione reale(dimostrata che deve esserci per forza anch una componente y in questo caso mi fa comunque strano.., lo prendo per dato di fatto, quindi il perno la mantiene anche in verticale)

poi te hai considerato la massa del corpo appeso direttamente in N(perchè F=m*a), quindi dovrebbe già comprendere i 9,8(g), giusto?

[axpgn]

"75america":poi te hai considerato la massa del corpo appeso direttamente in N(perchè F=m*a), quindi dovrebbe già comprendere i 9,8(g), giusto?

Non l'ho proprio considerata la massa di quel corpo, non mi serve ...
L'equazione è una sommatoria di momenti cioè forze per distanze (vettoriali); se una forza ce l'ho già, perché mi devo preoccupare della massa?

L'asta si muove a seconda della forze che agiscono su di essa ed il perno (più del muro) reagisce alle forze che agiscono su di esso; quindi a priori non sai come si muoveranno; io ti facevo l'esempio di "togliere il muro" per darti un'idea intuitiva del fatto che ci siano forze esercitate dal perno, sia orizzontali che verticali.

[75america]

mettiamo il caso di una sollecitazione in verticale sull'asta sicurmante esercitata dal blocchetto di 200N, quindi il perno(non il muro) reagisce con la sua componente $R_(py)$, credo di aver capito

[Rob995]

Posso solo confermare quello che dice axpgn: sì il vincolo reagisce con una forza a due componenti, x e y. Ti ripeto se prendi un bastone in mano e appendi qualcosa all'estremo dovrai esercitare una forza verticale per mantenerlo stabile. La orizzontale entra il gioco se, come qui, un altro perno è in grado di supportare il tuo sforzo, esercitando però una forza che abbia una componente orizzontale. Come diceva axpgn se però avessi attaccato all'estremo del bastone un filo perfettamente verticale, la forza esercitata da te all'estremo sarebbe stata solo verticale; perché? Poi per concludere, una corda ideale esercita forze solo ed esclusivamente lungo la direzione in cui è tesa. Un asta di ferro o un qualunque altro vincolo esulano da questa regola. Spero di essere stato d'aiuto nella discussione..