Integrale reale improprio da risolvere col teorema dei residui
$int_{RR} (cos(x)+1)/(1+x^2) dx$
la funzione integranda ha ordine di infinitesimo 2, pertanto l'integrale converge, provo a calcolarlo usando il teorema dei residui, cioè l'integrale deve essere uguale al prodotto del fattore $2 pi i$ per la sommatoria dei residui delle singolarità con parte immaginaria positiva della funzione integranda estesa al campo complesso.
$f(z)=(cos(z)+1)/(1+z^2) $
le singolarità sono due $z=+-i$, per quanto sopra detto considero solamente $z=i$, è un polo semplice, ne calcolo il residuo:
$Res f(z)|_(z=i) = lim_(z->i) (z-i) (cos(z)+1)/((z-i) (z+i))=1/(2i) (e^(i^2)+e^(-i^2)+2)/2=1/(2i) (e^2+1+2 e )/(2e)$
da cui:
$int_{RR} (cos(x)+1)/(1+x^2) dx= 2 pi i (1/(2i) (e^2+1+2 e )/(2e))= pi (e^2+1+2 e )/(2e)$
ma il mio risultato per wolfram è sbagliato, pur non essendo molto diverso da quello corretto
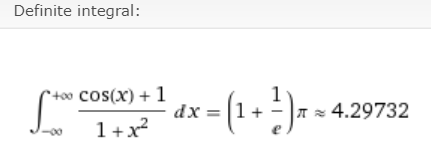
non riesco a capire dove ho sbagliato, perché wolfram al tempo stesso conferma il mio calcolo del residuo
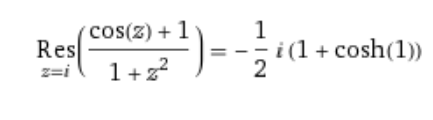
mi sfugge qualche altro punto di singolarità?
la funzione integranda ha ordine di infinitesimo 2, pertanto l'integrale converge, provo a calcolarlo usando il teorema dei residui, cioè l'integrale deve essere uguale al prodotto del fattore $2 pi i$ per la sommatoria dei residui delle singolarità con parte immaginaria positiva della funzione integranda estesa al campo complesso.
$f(z)=(cos(z)+1)/(1+z^2) $
le singolarità sono due $z=+-i$, per quanto sopra detto considero solamente $z=i$, è un polo semplice, ne calcolo il residuo:
$Res f(z)|_(z=i) = lim_(z->i) (z-i) (cos(z)+1)/((z-i) (z+i))=1/(2i) (e^(i^2)+e^(-i^2)+2)/2=1/(2i) (e^2+1+2 e )/(2e)$
da cui:
$int_{RR} (cos(x)+1)/(1+x^2) dx= 2 pi i (1/(2i) (e^2+1+2 e )/(2e))= pi (e^2+1+2 e )/(2e)$
ma il mio risultato per wolfram è sbagliato, pur non essendo molto diverso da quello corretto
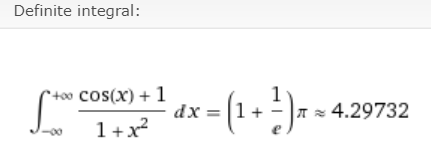
non riesco a capire dove ho sbagliato, perché wolfram al tempo stesso conferma il mio calcolo del residuo
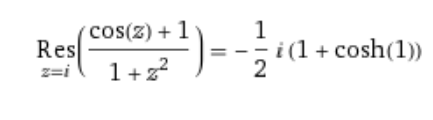
mi sfugge qualche altro punto di singolarità?
Risposte
Il problema è proprio la scelta di $cos z$ come funzione complessa ausiliaria.
Non va bene.
Devi usare un esponenziale, perché altrimenti il lemma di Jordan non funziona.
Non va bene.
Devi usare un esponenziale, perché altrimenti il lemma di Jordan non funziona.
"gugo82":
Il problema è proprio la scelta di $cos z$ come funzione complessa ausiliaria.
Non va bene.
Devi usare un esponenziale, perché altrimenti il lemma di Jordan non funziona.
grazie, con questo tuo suggerimento credo ora d'aver capito.
sfruttando la formula di Eulero, come funzione complessa ausiliaria considero:
$f(z)= (e^(iz)+1)/((z-i)(z+i))$
data la singolarità in $z=i$, considero l'integrale di $f(z)$ sulla frontiera percorsa in senso antiorario della metà superiore di un cerchio di raggio $R>|i|$ e centrato nell'origine del piano complesso, scompongo il dominio di integrazione in due: la semicirconferenza e l'intervallo appartenente all'asse reale $[-R,R]$ (cioè un diametro)
$int_{delSemiCer(R)} f(z) dz=int_{SemiCir(R)} f(z) dz+int_{-R}^{R} f(x) dx $
analizzo i 3 integrali nella precedente equazione:
$(*)$ l'integrale a primo membro si può calcolare col teorema dei residui:
$int_{delSemiCer(R)} (e^(iz)+1)/((z-i)(z+i)) dz= 2 pi i Res(f(z))|_(z=i) =pi (1 + e^-1)$
$(*)$ Considerando il limite $R->+infty$, per il lemma di Jordan il primo integrale a secondo membro diviene nullo.
$(*)$ il secondo integrale a secondo membro si scompone mediante la formula di eulero:
$int_{-R}^{R} (e^(ix)+1)/((x-i)(x+i)) dx=int_{-R}^{R} (cos(x)+1)/((x-i)(x+i)) dx+i int_{-R}^{R} sin(x)/((x-i)(x+i)) dx$
l'integrale col seno è nullo in quanto integrale su un dominio simmetrico di una funzione dispari, invece l'integrale col coseno è proprio ciò che sto cercando.
Quindi, passando al limite $R->+infty$ si ha:
$int_{-infty}^{+infty} (cos(x)+1)/((x-i)(x+i))= int_{delSemiCer(R)} (e^(iz)+1)/((z-i)(z+i)) dz =pi (1 + e^-1) $
che è lo stesso risultato risultato di Wolfram.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo