Integrale con funzioni polidrome
Utilizzando il teorema dei residui calcolare $\int_{0}^{+\infty}\frac{\sqrt{x}\log(x)}{x^3-1}dx$.
Questo è il mio tentativo.
La prima osservazione è che l'integranda è sommabile su $(0,+\infty)$.
Poniamo $f(z)=\frac{\sqrt{z}\log(z)}{z^3-1}$ dove per $\sqrt{z}$ e $\log(z)$ scegliamo la stessa determinazione, imponendo $\arg(z)\in [0,2\pi)$.
Ora, $f(z)$ ha in $z=0$ un punto di diramazione (non credo sia ulteriormente classificabile), in $z=1$ una singolarità eliminabile, in $z=e^{\frac{i2\pi}{3}},e^{\frac{i4\pi}{3}}$ due poli semplici.
Consideriamo il seguente dominio:
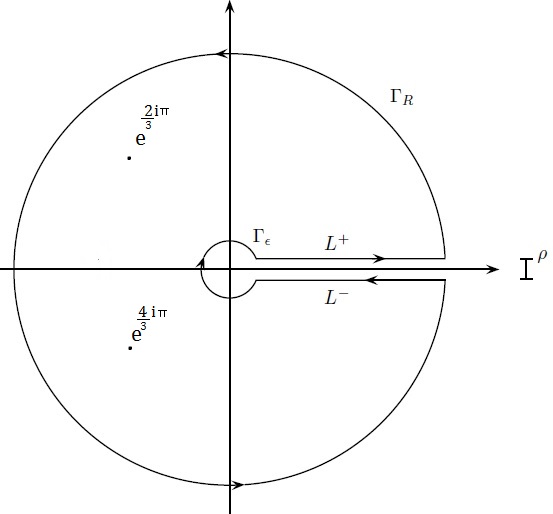
Quindi
$\lim_{\rho \to 0} \int_{L^+}\frac{\sqrt{z}\log(z)}{z^3-1}dz=\int_{\epsilon}^{R}\frac{\sqrt{x}\log(x)}{x^3-1}dx$,
$\lim_{\rho \to 0} \int_{L^-}\frac{\sqrt{z}\log(z)}{z^3-1}dz=-\int_{\epsilon}^{R}\frac{\sqrt{xe^{i2\pi}}(\log(x)+i2\pi)}{x^3-1}dx=\int_{\epsilon}^{R}\frac{\sqrt{x}(\log(x)+i2\pi)}{x^3-1}dx$.
Applicando rispettivamente i lemmi del piccolo e grande cerchio, otteniamo che gli integrali estesi a $\Gamma_{\epsilon}$ e $\Gamma_{R}$, valutati al limite, sono nulli.
In conclusione, applichiamo il teorema dei residui (passando al limite per $\epsilon$ che tende a $0$, $R$ che tende a $+\infty$:
$\int_{0}^{+\infty}\frac{\sqrt{x}\log(x)}{x^3-1}dx+\int_{0}^{+\infty}\frac{\sqrt{x}(\log(x)+i2\pi)}{x^3-1}dx=i2\pi(R[e^{\frac{i2\pi}{3}}]+R[e^{\frac{i4\pi}{3}}]).$
Ora passiamo a calcolare i residui (poniamo $z_0=e^{\frac{i2\pi}{3}}$):
$R[z_0]=\lim_{z \to z_0}(z-z_0) \frac{\sqrt{z}\log(z)}{z^3-1}= \frac{\sqrt{z_0}\log(z_0)}{3{z_0}^2}=\frac{z_0\sqrt{z_0}\log(z_0)}{3}=-i\frac{2\pi}{9}.$
In maniera simile
$R[z_0^2]=i\frac{4\pi}{9}.$
In conclusione
$2\int_{0}^{+\infty}\frac{\sqrt{x}\log(x)}{x^3-1}dx+i2\pi\int_{0}^{+\infty}\frac{\sqrt{x}}{x^3-1}dx=-\frac{4\pi^2}{9}$
Prendendo la parte reale si ha
$\int_{0}^{+\infty}\frac{\sqrt{x}\log(x)}{x^3-1}dx=-\frac{2\pi^2}{9}$.
che è palesemente sbagliato!!! Il risultato non può essere negativo! La risposta corretta è $\frac{\pi^2}{9}$. Qualcuno può aiutarmi a trovare l'errore? Non lo riesco a trovare.
Questo è il mio tentativo.
La prima osservazione è che l'integranda è sommabile su $(0,+\infty)$.
Poniamo $f(z)=\frac{\sqrt{z}\log(z)}{z^3-1}$ dove per $\sqrt{z}$ e $\log(z)$ scegliamo la stessa determinazione, imponendo $\arg(z)\in [0,2\pi)$.
Ora, $f(z)$ ha in $z=0$ un punto di diramazione (non credo sia ulteriormente classificabile), in $z=1$ una singolarità eliminabile, in $z=e^{\frac{i2\pi}{3}},e^{\frac{i4\pi}{3}}$ due poli semplici.
Consideriamo il seguente dominio:

Quindi
$\lim_{\rho \to 0} \int_{L^+}\frac{\sqrt{z}\log(z)}{z^3-1}dz=\int_{\epsilon}^{R}\frac{\sqrt{x}\log(x)}{x^3-1}dx$,
$\lim_{\rho \to 0} \int_{L^-}\frac{\sqrt{z}\log(z)}{z^3-1}dz=-\int_{\epsilon}^{R}\frac{\sqrt{xe^{i2\pi}}(\log(x)+i2\pi)}{x^3-1}dx=\int_{\epsilon}^{R}\frac{\sqrt{x}(\log(x)+i2\pi)}{x^3-1}dx$.
Applicando rispettivamente i lemmi del piccolo e grande cerchio, otteniamo che gli integrali estesi a $\Gamma_{\epsilon}$ e $\Gamma_{R}$, valutati al limite, sono nulli.
In conclusione, applichiamo il teorema dei residui (passando al limite per $\epsilon$ che tende a $0$, $R$ che tende a $+\infty$:
$\int_{0}^{+\infty}\frac{\sqrt{x}\log(x)}{x^3-1}dx+\int_{0}^{+\infty}\frac{\sqrt{x}(\log(x)+i2\pi)}{x^3-1}dx=i2\pi(R[e^{\frac{i2\pi}{3}}]+R[e^{\frac{i4\pi}{3}}]).$
Ora passiamo a calcolare i residui (poniamo $z_0=e^{\frac{i2\pi}{3}}$):
$R[z_0]=\lim_{z \to z_0}(z-z_0) \frac{\sqrt{z}\log(z)}{z^3-1}= \frac{\sqrt{z_0}\log(z_0)}{3{z_0}^2}=\frac{z_0\sqrt{z_0}\log(z_0)}{3}=-i\frac{2\pi}{9}.$
In maniera simile
$R[z_0^2]=i\frac{4\pi}{9}.$
In conclusione
$2\int_{0}^{+\infty}\frac{\sqrt{x}\log(x)}{x^3-1}dx+i2\pi\int_{0}^{+\infty}\frac{\sqrt{x}}{x^3-1}dx=-\frac{4\pi^2}{9}$
Prendendo la parte reale si ha
$\int_{0}^{+\infty}\frac{\sqrt{x}\log(x)}{x^3-1}dx=-\frac{2\pi^2}{9}$.
che è palesemente sbagliato!!! Il risultato non può essere negativo! La risposta corretta è $\frac{\pi^2}{9}$. Qualcuno può aiutarmi a trovare l'errore? Non lo riesco a trovare.
Risposte
Ciao Phantom96,
Non mi pare, mi risulta invece che si ha:
$R[e^{\frac{i4\pi}{3}}] = (2i\pi)/9 $
Hai tenuto conto del fatto che anche la radice quadrata cambia argomento di $2\pi $ sul bordo inferiore?
Ora non ho tempo di guardarci, ma mi pare che anche questo integrale possa risolversi in modo analogo a quello già visto qui.
"Phantom96":
In maniera simile
$R[z_0^2]=i\frac{4\pi}{9}$.
Non mi pare, mi risulta invece che si ha:
$R[e^{\frac{i4\pi}{3}}] = (2i\pi)/9 $
Hai tenuto conto del fatto che anche la radice quadrata cambia argomento di $2\pi $ sul bordo inferiore?
Ora non ho tempo di guardarci, ma mi pare che anche questo integrale possa risolversi in modo analogo a quello già visto qui.
$ 2\int_{0}^{+\infty}\frac{\sqrt{x}\log(x)}{x^3-1}dx+i2\pi\int_{0}^{+\infty}\frac{\sqrt{x}}{x^3-1}dx=-\frac{4\pi^2}{9} $
Prendendo la parte reale si ha ...
Non puoi liberarti cosi' facilmente della parte immaginaria.* Purtroppo anche quel pezzo li fa parte del risultato. Occorre calcolare anche l'integrale della parte "immaginaria" (in modo uguale a quello gia' fatto) e quindi includere anche il suo risultato.
Alla fine il risultato complessivo deve essere puramente reale.
* Ammesso che sia veramente immaginaria !
In realtà sono riuscito a risolvere.
Il problema è che $z=1$ diventa polo semplice quando cambio ramo. Quindi a $L^-$ va aggiunta una semicirconferenza sotto $z=1$. Facendo così il risultato viene. L'altro integrale, con questa osservazione, ha perfettamente senso perchè è inteso nel senso del valor principale di Cauchy (viene 0).
Volendo c'era un modo più semplice di scegliere il dominio, ma ci ho pensato solo dopo. Ovvero un settore circolare di centro l'origine e ampiezza $\frac{2\pi}{3}$ "aggiungendo" una semcirconferenza in corrispondenza di $z=e^{\frac{12\pi}{3}}$.
Il problema è che $z=1$ diventa polo semplice quando cambio ramo. Quindi a $L^-$ va aggiunta una semicirconferenza sotto $z=1$. Facendo così il risultato viene. L'altro integrale, con questa osservazione, ha perfettamente senso perchè è inteso nel senso del valor principale di Cauchy (viene 0).
Volendo c'era un modo più semplice di scegliere il dominio, ma ci ho pensato solo dopo. Ovvero un settore circolare di centro l'origine e ampiezza $\frac{2\pi}{3}$ "aggiungendo" una semcirconferenza in corrispondenza di $z=e^{\frac{12\pi}{3}}$.
La situazione è analoga a quella che si può osservare ad esempio qui.
Più in generale si ha:
\begin{equation}
\boxed{\int_0^{+\infty} \frac{x^{a + \frac{1}{2}} \log(x)}{x^3 - 1} \,\text{d}x = \frac{\pi^2}{9} \sec^2 \bigg(\frac{a \pi}{3}\bigg) }
\end{equation}
per $\text{Re}[a] > - 3/2 $
Nel caso particolare $a = 0 > - 3/2 $ si ottiene il risultato dell'integrale proposto:
\begin{equation}
\boxed{\int_0^{+\infty} \frac{\sqrt{x} \log(x)}{x^3 - 1} \,\text{d}x = \frac{\pi^2}{9} }
\end{equation}
Più in generale si ha:
\begin{equation}
\boxed{\int_0^{+\infty} \frac{x^{a + \frac{1}{2}} \log(x)}{x^3 - 1} \,\text{d}x = \frac{\pi^2}{9} \sec^2 \bigg(\frac{a \pi}{3}\bigg) }
\end{equation}
per $\text{Re}[a] > - 3/2 $
Nel caso particolare $a = 0 > - 3/2 $ si ottiene il risultato dell'integrale proposto:
\begin{equation}
\boxed{\int_0^{+\infty} \frac{\sqrt{x} \log(x)}{x^3 - 1} \,\text{d}x = \frac{\pi^2}{9} }
\end{equation}


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo