Minimi quadrati
Buongiorno, sono alle prese con un problema pratico dove devo utilizzare degli strumenti dell'analisi numerica, e vorrei chiedervi un consiglio su come fare.
Ho studiato in maniera analitica il rendimento di una turbina ed è emerso che la curva che ne descrive l'andamento in funzione della velocità di rotazione è una parabola passante per l'origine (a turbina frema il rendimento è nullo).
Poi in laboratorio ho raccolto dei dati sperimentali ed in effetti l'andamento rispecchia approssimativamente il modello teorico.
Vorrei trovare la curva che descrive il fenomeno e ho pensato di farlo in matlab utilizzando il metodo dei minimi quadrati. Ho delle coppie di punti $(x_n,y_n)$ nel piano cartesiano, e cerco di trovare il polinomio di secondo grado che più si avvicina al loro andamento.
Tutto ciò non è complicato e l'ho già fatto con il comando $"polyfit"(x,y,2)$, soltanto che la parabola trovata non passa per l'origine a causa di errori sperimentali.
Dunque vorrei imporre il passaggio per l'origine prima di trovare la soluzione ai minimi quadrati, ma non so come fare
Per caso sapete se in matlab esiste qualche funzione per questo, oppure qualche stratagemma per risolvere il problema?
Grazie in anticipo, Lorenzo
Ho studiato in maniera analitica il rendimento di una turbina ed è emerso che la curva che ne descrive l'andamento in funzione della velocità di rotazione è una parabola passante per l'origine (a turbina frema il rendimento è nullo).
Poi in laboratorio ho raccolto dei dati sperimentali ed in effetti l'andamento rispecchia approssimativamente il modello teorico.
Vorrei trovare la curva che descrive il fenomeno e ho pensato di farlo in matlab utilizzando il metodo dei minimi quadrati. Ho delle coppie di punti $(x_n,y_n)$ nel piano cartesiano, e cerco di trovare il polinomio di secondo grado che più si avvicina al loro andamento.
Tutto ciò non è complicato e l'ho già fatto con il comando $"polyfit"(x,y,2)$, soltanto che la parabola trovata non passa per l'origine a causa di errori sperimentali.
Dunque vorrei imporre il passaggio per l'origine prima di trovare la soluzione ai minimi quadrati, ma non so come fare
Per caso sapete se in matlab esiste qualche funzione per questo, oppure qualche stratagemma per risolvere il problema?
Grazie in anticipo, Lorenzo
Risposte
Io farei una semplice sottrazione. Proprio nel modo più brutale possibile:
zstar=polyfit(x, y, 2); z=zstar-zstar(1);
Haha, è vero, così passa di sicuro per l'origine 
Il problema è che il ragionamento dell'interpolazione ai minimi quadrati va un po'a farsi benedire
Comunque in questo caso la parabola trovata col metodo dei minimi quadrati per fortuna non si allontana molto dall'origine, quindi se uso questo stratagemma nessuno se ne accorgerà! Ti ringrazio molto perchè non ci avevo proprio pensato.
Ad ogni modo, se a qualcuno viene in mente un metodo rigoroso sarei curioso di capire come fare, anche per una questione di interesse mio personale
Il problema è che il ragionamento dell'interpolazione ai minimi quadrati va un po'a farsi benedire
Comunque in questo caso la parabola trovata col metodo dei minimi quadrati per fortuna non si allontana molto dall'origine, quindi se uso questo stratagemma nessuno se ne accorgerà! Ti ringrazio molto perchè non ci avevo proprio pensato.
Ad ogni modo, se a qualcuno viene in mente un metodo rigoroso sarei curioso di capire come fare, anche per una questione di interesse mio personale
Ma non stiamo barando, facendo così. E' una procedura che si usa, o almeno, così mi risulta (non ho mai studiato granché di matematica applicata, purtroppo). Il concetto è che c'è un "rumore di fondo" presente nelle misure e lo dobbiamo sottrarre via prima di potere usare i risultati.
Ho provato con il tuo metodo ma purtroppo non va bene 
Il fatto è che per x=0 il polinomio vale -0.4, e dal momento che la curva descrive un rendimento, compreso sempre tra 0 e 1, risulta essere troppo da aggiungere e "sballa" tutti i dati.
A questo punto penso toccherà fare un piccolo script. Il generico polinomio il cui grafico passa per l'origine è "ax^2+bx+0", e quindi in qualche modo dovrei andare a ricondurmi a risolvere un sistema ai minimi quadrati dove però le incognite sono soltanto $a$ e $b$.
Domani mattina cerco i quaderni di analisi numerica e provo a buttare giù qualcosa, che ora non mi ricordo le funzioni a memoria..
Il fatto è che per x=0 il polinomio vale -0.4, e dal momento che la curva descrive un rendimento, compreso sempre tra 0 e 1, risulta essere troppo da aggiungere e "sballa" tutti i dati.
A questo punto penso toccherà fare un piccolo script. Il generico polinomio il cui grafico passa per l'origine è "ax^2+bx+0", e quindi in qualche modo dovrei andare a ricondurmi a risolvere un sistema ai minimi quadrati dove però le incognite sono soltanto $a$ e $b$.
Domani mattina cerco i quaderni di analisi numerica e provo a buttare giù qualcosa, che ora non mi ricordo le funzioni a memoria..
Puoi usare un solver per l'ottimizzazione (es. AMPL o non so se anche matlab o mathematica possano farlo) che ti minimizzi lo scarto ai minimi quadrati:
$ min_{a,b} sum_(i) (y_i - (a*x_i^2 + b*x_i))^2 $
Così non hai bisogno di implementare algoritmi o cose del genere. Comunque in matlab ci saranno sicuramente librerie con all'interno metodi già implementati come ad es. Gauss–Newton.
$ min_{a,b} sum_(i) (y_i - (a*x_i^2 + b*x_i))^2 $
Così non hai bisogno di implementare algoritmi o cose del genere. Comunque in matlab ci saranno sicuramente librerie con all'interno metodi già implementati come ad es. Gauss–Newton.
Ho trovato che il comando per cercare il minimo di una funzione a più variabili è $"fminsearch(f,v)"$ con $f$ la funzione di cui cerco il minimo e $v$ un punto vicino al quale voglio cercare il minimo stesso.
Ho scritto la funzione utilizzando il prodotto riga colonna la posto della sommatoria:
Ora però se provo a minimizzare la funzione ottengo errori
Penso sia dovuto a come ho definito la funzione, perchè nell'esempio che ho trovato veniva usato il comando $"function"$, ma nel mio contesto se definivo la funzione $f$ col comando function mi venivano fuori altri errori :s
Ho scritto la funzione utilizzando il prodotto riga colonna la posto della sommatoria:
f=inline('(y-(a.*x.^2+b.*x).^2)*ones','a','b') dove x de y sono vettori riga 1x8 (devo inperpolare 8 valori) e ones è un vettore colonna 8x1 con tutti gli elementi che valgono 1.Ora però se provo a minimizzare la funzione ottengo errori
>> fminsearch(f,[0,0])
??? Error using ==> inline.subsref at 14
Not enough inputs to inline function.
Error in ==> fminsearch at 205
fv(:,1) = funfcn(x,varargin{:});
Penso sia dovuto a come ho definito la funzione, perchè nell'esempio che ho trovato veniva usato il comando $"function"$, ma nel mio contesto se definivo la funzione $f$ col comando function mi venivano fuori altri errori :s
No, no, non usare quella cosa là!!! 
Quel comando serve per minimizzare funzioni non lineari e usa algoritmi molto più incasinati del linearissimo metodo dei minimi quadrati. Guarda, secondo me fai prima a scriverti una piccola function che fa quello che vuoi tu. Risolvere il problema dei minimi quadrati è in ultima analisi risolvere un sistema di equazioni lineari, non occorrono grandi manovre.
Quel comando serve per minimizzare funzioni non lineari e usa algoritmi molto più incasinati del linearissimo metodo dei minimi quadrati. Guarda, secondo me fai prima a scriverti una piccola function che fa quello che vuoi tu. Risolvere il problema dei minimi quadrati è in ultima analisi risolvere un sistema di equazioni lineari, non occorrono grandi manovre.
Il fatto è che non so bene come fa matlab a risolvere i minimi quadrati. So che per risolvere un sistema $Ax=b$ la matrice $A$ viene divisa con la fattorizzazione QR, cioè $A=QR$ con Q quadrata e R rettangolare. Poi si calcola il residuo e lo si minimizza, ma a qual punto non so che algoritmo viene usato per minimizzarlo..
Ops, scusami ma non so perché ti ho indicato il metodo per risolvere i minimi quadrati in generale, ovviamente in un caso lineare come questo usare qualcosa come Gauss-Newton è fuori luogo come dice dissonance.
Supponiamo di avere $m$ coppie $(x_i,y_i)$; è sufficiente costruire la matrice $m times 2$ $X$ formata da elementi $X_{ij} = x_i^j$ (ovvero una matrice costituita da due colonne: la prima contente tutte le $x_i$ la seconda le $x_i$ elevate al quadrato) e il vettore delle incognite $beta = (b, a)^T$. Quello che vorresti fare è risolvere il sistema $X beta = y$ dove $y = (y_1, ... , y_m)^T$. Ovviamente tale sistema non avrà soluzione. Vuoi quindi trovare il vettore $beta$ che più si avvicina a tale soluzione (che minimizza gli scarti quadratici). Con qualche semplice passaggio algebrico si può dimostrare che tale vettore è $beta = (X^T X)^{-1} X^T y$.
Non c'è bisogno quindi di usare nessun algoritmo, costruisci la matrice $X$ e il vettore $y$ e sei a posto.
Supponiamo di avere $m$ coppie $(x_i,y_i)$; è sufficiente costruire la matrice $m times 2$ $X$ formata da elementi $X_{ij} = x_i^j$ (ovvero una matrice costituita da due colonne: la prima contente tutte le $x_i$ la seconda le $x_i$ elevate al quadrato) e il vettore delle incognite $beta = (b, a)^T$. Quello che vorresti fare è risolvere il sistema $X beta = y$ dove $y = (y_1, ... , y_m)^T$. Ovviamente tale sistema non avrà soluzione. Vuoi quindi trovare il vettore $beta$ che più si avvicina a tale soluzione (che minimizza gli scarti quadratici). Con qualche semplice passaggio algebrico si può dimostrare che tale vettore è $beta = (X^T X)^{-1} X^T y$.
Non c'è bisogno quindi di usare nessun algoritmo, costruisci la matrice $X$ e il vettore $y$ e sei a posto.
Grazie, diciamo che ho capito sino al penultimo passaggio
Da come ho capito io, se ad esempio i miei punti trovati sperimentalmente sono $(2,1)$, $(5,2)$ $(7,3)$ la matrice $X$ ed il vettore $y$ valgono:
$X=((2," "4),(5," "25),(7," "49))$
$y=(1,2,3)^T$
Ora risolvendo $beta = (X^T X)^{-1} X^T y$ la soluzione che ottengo è proprio quella ai minimi quadrati, senza risolvere priblemi di massimo e minimo o cose simili?
Ora comunque provo ad implementare tutto in Matlab e vedo come va
Da come ho capito io, se ad esempio i miei punti trovati sperimentalmente sono $(2,1)$, $(5,2)$ $(7,3)$ la matrice $X$ ed il vettore $y$ valgono:
$X=((2," "4),(5," "25),(7," "49))$
$y=(1,2,3)^T$
Ora risolvendo $beta = (X^T X)^{-1} X^T y$ la soluzione che ottengo è proprio quella ai minimi quadrati, senza risolvere priblemi di massimo e minimo o cose simili?
Ora comunque provo ad implementare tutto in Matlab e vedo come va
"anonymous_ed8f11":
Ora risolvendo $beta = (X^T X)^{-1} X^T y$ la soluzione che ottengo è proprio quella ai minimi quadrati, senza risolvere priblemi di massimo e minimo o cose simili?
Sì perché quella formula è già la soluzione del problema di minimo. Se tu derivi e poni uguale al vettore nullo otterrai quell'equazione. Guarda qui.
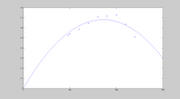
Ecco fatto, ho fatto il disegno della parabola 
I dati sperimentali sono quelli coi tondini, e la parabola non li segue molto a causa dei probabili errori sperimentali, comunque il risultato era quello che volevo!
Vi ringrazio di cuore per tutto l'aiuto fornitomi
I dati sperimentali sono quelli coi tondini, e la parabola non li segue molto a causa dei probabili errori sperimentali, comunque il risultato era quello che volevo!
Vi ringrazio di cuore per tutto l'aiuto fornitomi
"Deckard":
Ovviamente tale sistema non avrà soluzione. Vuoi quindi trovare il vettore $beta$ che più si avvicina a tale soluzione (che minimizza gli scarti quadratici). [...]
Su questo argomento tempo fa ho scritto un piccolo riassunto di teoria, magari ti può servire:
post388426.html#p388426
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo