Studio carattere serie

[rocco.g1]

ciao,
ragazzi purtroppo io non ho molte infos sul mio libro e quindi non so bene come fare lo studio del carattere della serie...

ad esempio io faccio di solito così:

avendo una serie di leibniz vedo se è decrescente ed il suo limite è convergente...

mi calcolo il segno della derivata e vedo se è positivo o negativo, in questo caso dico che cresce o decresce, e poi mi calcolo il limite...

inoltre verifico anke che A(n) > A(n+1) o meno...

e poi do le conclusioni... ma è corretto fare così ?

[rocco.g1]

help please

[Angela41]

sì ma il limite deve essere 0

[rocco.g1]

mmm si... hai ragione...

e per il resto ?

il fatto di usare la derivata per determinare la decrescenza o meno è fattibile ?

[Angela41]

secondo me derivare in N non è accettabile come dimostrazione,meglio farlo senza
ciao

[rocco.g1]

e senza come posso fare ?

cioè per studiare la decrescenza... non conosco altri metodi...

[Angela41]

devi vedere se è sempre verificata la disequazione a(n)>a(n+1)
per esempio se hai a(n)=1/n^2 devi risolvere (1/n^2)>(1/(n+1)^2) e vedere se vale per ogni n (o almeno da qualche n in poi)
ciao

[rocco.g1]

mm ok...

però per farlo, perchè anke io sapevo questo metodo, non capisco come si faccia a stabilire che an > a(n+1) ... ad esempio con questa serie:



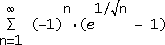
come faccio a sapere se è maggiore o minore ?

[Principe2]

quello che dice angela è corretto; se proprio vuoi derivare, potresti fare il seguente ragionamento; sostituisci x alla n e consideri la funzione che ottieni che puoi derivare; supponiamo che sia decrescente, allora è noto (ovvio più che noto!) che se una funzione è decrescente, allora è decrescente ogni successione di punti estraibili della funzione; quindi, in particolare, è decrescente la successione dove i punti che scegli sono le immagini dei naturali.

ciao, ubermensch

[rocco.g1]

uber mi fai l'esempio ( se ti va ... ) sulla serie che ho postato su ? così capisco meglio...

[Angela41]

xchè viene (e^(1/radice(n))-1) > (e^(1/radice(n+1))-1) il -1 lo semplifichi poi dividi per e^(1/radice(n+1)) (dato che è sempre > 0)quindi fai la differenza degli esponenti (1/radice(n)) - (1/radice(n+1)) che chiamiamo h e siccome il primo è sempre + grande del secondo la differenza è maggiore di 0 quindi e^h > 1 verificato
controlla che non sò se ho fatto giusto
ciao

[rocco.g1]

ok lo guardo e ti dico... grazie

[rocco.g1]

ok è perfetta... grazie a tutti e due per l'aiuto