Serie, è giusto ?
ciao,
di seguito riporto tutti i dubbi che ho ancora sulle serie...ditemi se il procedimento che ho scritto può andare bene:
1. Serie a termini alterni
se la successione è decrescente ed infinitesima, cioè lim n->inf.
da 0 allora la serie converge.
Per dimostrarlo posso calcolarmi la derivata e studiarla in x >0,
senza considerare quello che vi succede ad x<0 e vedere se è crescente o decrescente e poi vedere come si comporta all'inifinito ?
così sono sicuro di aver dimostrato la sua convergenza o divergenza ? inoltre se così fosse, se studio la derivata e mi esce che ad esempio da 0 ad 1/2 è crescente, poi da 1/2 a 3 è decrescente e poi da 3 all'infinito è crescente, devo valutare solo ilfatto che è crescente all'infinito e concludere che la serie diverge se il lim all'inifinito non tende a zero ? cioè della derivata devo considerare solo la decrescenza e la crescenza all'infinito e lasciare da parte gli intervalli finiti in cui cresce o decresce ?
2) Criterio della radice
se esiste il limite di (an)^(1/n)=l
la serie è assolutamente convergente se 1==0
non convergente se l > 1
indeterminata se l=1
mi va bene solo studiare il limite tendente all'inf. e vedere a cosa corrisponde ? senza fare ulteriori " accertamenti "? si può concludere direttamente la sua convergenza o divergenza ?
3) Criterio del rapporto
se esiste il limite all'inf. di | an+1 / an | = l
la serie converge o diverge a seconda del valore di l
Anke qui mi basta studiare solo il limite ?
4) se mi capita qualcosa del tipo:
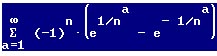
studiare la convergenza semplice ed assoluta al variare di a appartenente ad R
cosa mi tocca fare ? studio i tre casi separati con a > 0 e a >0 ed a = 0 e considerando poi la serie come una normale serie a termini alterni, sostituendo semplicemente il valore di a con un numero maggiore, minore o uguale a zero ?
grazie per l'aiuto...
di seguito riporto tutti i dubbi che ho ancora sulle serie...ditemi se il procedimento che ho scritto può andare bene:
1. Serie a termini alterni
se la successione è decrescente ed infinitesima, cioè lim n->inf.
da 0 allora la serie converge.
Per dimostrarlo posso calcolarmi la derivata e studiarla in x >0,
senza considerare quello che vi succede ad x<0 e vedere se è crescente o decrescente e poi vedere come si comporta all'inifinito ?
così sono sicuro di aver dimostrato la sua convergenza o divergenza ? inoltre se così fosse, se studio la derivata e mi esce che ad esempio da 0 ad 1/2 è crescente, poi da 1/2 a 3 è decrescente e poi da 3 all'infinito è crescente, devo valutare solo ilfatto che è crescente all'infinito e concludere che la serie diverge se il lim all'inifinito non tende a zero ? cioè della derivata devo considerare solo la decrescenza e la crescenza all'infinito e lasciare da parte gli intervalli finiti in cui cresce o decresce ?
2) Criterio della radice
se esiste il limite di (an)^(1/n)=l
la serie è assolutamente convergente se 1=
non convergente se l > 1
indeterminata se l=1
mi va bene solo studiare il limite tendente all'inf. e vedere a cosa corrisponde ? senza fare ulteriori " accertamenti "? si può concludere direttamente la sua convergenza o divergenza ?
3) Criterio del rapporto
se esiste il limite all'inf. di | an+1 / an | = l
la serie converge o diverge a seconda del valore di l
Anke qui mi basta studiare solo il limite ?
4) se mi capita qualcosa del tipo:

studiare la convergenza semplice ed assoluta al variare di a appartenente ad R
cosa mi tocca fare ? studio i tre casi separati con a > 0 e a >0 ed a = 0 e considerando poi la serie come una normale serie a termini alterni, sostituendo semplicemente il valore di a con un numero maggiore, minore o uguale a zero ?
grazie per l'aiuto...
Risposte
ragazzi aiutatemi...domani ho l'esame 
va beh non mi ha risposto nessuno... domani come andrà andrà...


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo