Risultato serie
ciao,
anche se questa serie sembra facile, non riesco a capire i passaggi per cui allafine esce come risultato 1/2... me lo spiegate perfavore ?
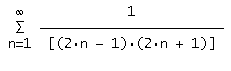
anche se questa serie sembra facile, non riesco a capire i passaggi per cui allafine esce come risultato 1/2... me lo spiegate perfavore ?
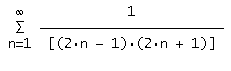
Risposte
quale serie!?
Luca.
Luca.
ciao,
scusami, ero su slackware e di sicuro si è verificato qualke errore quando ho inserito la img, cmq ora è tutto ok, la serie è quella postata sopra...
scusami, ero su slackware e di sicuro si è verificato qualke errore quando ho inserito la img, cmq ora è tutto ok, la serie è quella postata sopra...
Si', e' una serie telescopica, per la quale e' quesi immediato trovare la somma.
Infatti, in generale una serie telescopica e' una serie che ha come termine generale b_n=a_n-a_(n+1). Allora se sommi i b_n per n da 0 fino a k, ottieni a_0-a_k. Il limite di tale espressione per k che va a +infinito da', per definizione, la somma della serie data di termine generale b_n.
Nel tuo caso, se raccogli 1/2 e lo porti fuori, ti rimane una serie telescopica con a_n=1/(2n-1). Allora la sua somma parziale vale (credo che parta da 1) a_1-a_k=1-1/(2k-1) che tende a 1. Allora la somma vale effettivamente 1/2.
Luca.
Infatti, in generale una serie telescopica e' una serie che ha come termine generale b_n=a_n-a_(n+1). Allora se sommi i b_n per n da 0 fino a k, ottieni a_0-a_k. Il limite di tale espressione per k che va a +infinito da', per definizione, la somma della serie data di termine generale b_n.
Nel tuo caso, se raccogli 1/2 e lo porti fuori, ti rimane una serie telescopica con a_n=1/(2n-1). Allora la sua somma parziale vale (credo che parta da 1) a_1-a_k=1-1/(2k-1) che tende a 1. Allora la somma vale effettivamente 1/2.
Luca.
grazie Luca! 
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo