Per allenarsi sulle equadiff e non solo
Per quanto riguarda il seguente problema di Cauchy:
$y' = \sin (y)$
$y(0) = (11 \pi)/2$
- ha una ed una sola soluzione massimale?
- in caso di risposta affermativa alla precedente domanda, essa è definita su tutto $RR$?
- sempre se esiste una soluzione massimale, trovarne una espressione analitica (ricordo che l'integrale di $1/\sin (t)$ è immediato, grazie alle cosiddette "formule parametriche")
ciao
$y' = \sin (y)$
$y(0) = (11 \pi)/2$
- ha una ed una sola soluzione massimale?
- in caso di risposta affermativa alla precedente domanda, essa è definita su tutto $RR$?
- sempre se esiste una soluzione massimale, trovarne una espressione analitica (ricordo che l'integrale di $1/\sin (t)$ è immediato, grazie alle cosiddette "formule parametriche")
ciao
Risposte
Ragazzi
reduce da un paio di settimane passate sulle Dolomiti [allietate come non mai in precedenza ricordavo dallo smog prodotto dalle interminabili carovane di autoveicoli in movimento perenne 24 ore su 24
…] ‘quello che scrive bestialità’ è di nuovo felicemente tra voi…
Uno dei miei primi pensieri è stato naturalmente quello di andare a rivedere il post di Patrone, soprattutto perché nel problema da lui impostato mi sembrava ci fosse qualcosa di ‘dejà vue’. L’equazione da lui proposta all’inizio è [all’incirca] la seguente…
$y’=sin y$ con $y(0)=-pi/2$ (1)
Si tratta di una equazione differenziale nella quale la derivata $y’$ è funzione della sola $y$ [e non della $x$…] e questo ricordavo che in passato aveva dato luogo a problemi un poco ‘insoliti’. Andando a rivedermi i ‘vecchi postati’ alla fine ho trovato quello che cercavo. Si tratta di una ‘discussione’ avutasi due anni e mezzo fa tra Luca, ubermensch e lo scrivente intorno ad una equazione differenziale del tipo…
$y’= g(y)$ con $y(0)=y_0$ (2)
… tipologia a cui la (1) evidentemente appartiene. Come tutte le discussioni tra Luca e lo scrivente è finita ‘in parità’, nel senso che non ha portato vantaggio né a loro né agli altri membri del forum
… Polemiche a parte mi parebbe utile cosa riaprire quella discussione… anche perché rivedendo la cosa mi sono accorto di aver scritto in quella circostanza una castroneria alla quale vorrei cercare [umilmente...] di porre rimedio…
Per dovere di ‘paternità’ chiedo a Patrone [scusate il gioco di parole
...] se ritiene opportuno procedere su questo stesso topic oppure aprirne un altro…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
reduce da un paio di settimane passate sulle Dolomiti [allietate come non mai in precedenza ricordavo dallo smog prodotto dalle interminabili carovane di autoveicoli in movimento perenne 24 ore su 24
…] ‘quello che scrive bestialità’ è di nuovo felicemente tra voi… Uno dei miei primi pensieri è stato naturalmente quello di andare a rivedere il post di Patrone, soprattutto perché nel problema da lui impostato mi sembrava ci fosse qualcosa di ‘dejà vue’. L’equazione da lui proposta all’inizio è [all’incirca] la seguente…
$y’=sin y$ con $y(0)=-pi/2$ (1)
Si tratta di una equazione differenziale nella quale la derivata $y’$ è funzione della sola $y$ [e non della $x$…] e questo ricordavo che in passato aveva dato luogo a problemi un poco ‘insoliti’. Andando a rivedermi i ‘vecchi postati’ alla fine ho trovato quello che cercavo. Si tratta di una ‘discussione’ avutasi due anni e mezzo fa tra Luca, ubermensch e lo scrivente intorno ad una equazione differenziale del tipo…
$y’= g(y)$ con $y(0)=y_0$ (2)
… tipologia a cui la (1) evidentemente appartiene. Come tutte le discussioni tra Luca e lo scrivente è finita ‘in parità’, nel senso che non ha portato vantaggio né a loro né agli altri membri del forum
… Polemiche a parte mi parebbe utile cosa riaprire quella discussione… anche perché rivedendo la cosa mi sono accorto di aver scritto in quella circostanza una castroneria alla quale vorrei cercare [umilmente...] di porre rimedio… Per dovere di ‘paternità’ chiedo a Patrone [scusate il gioco di parole
...] se ritiene opportuno procedere su questo stesso topic oppure aprirne un altro… cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
nessun problema di paternità, of course.
valuta tu quale sia la soluzione migliore per dicutere il topic. Forse uno nuovo potrebbe essere meglio. Ma la cosa importante à che un thread sia "vivo" e quindi appaia all'inizio dell'elenco...
Comunque, forse un nuovo post con titolo adatto opera una migliore selezione dei "lettori". E' un caso di equlibrio "separating", indotto da un segnale veridico. Tanto per non dimanticarmi il mestiere
ciao
valuta tu quale sia la soluzione migliore per dicutere il topic. Forse uno nuovo potrebbe essere meglio. Ma la cosa importante à che un thread sia "vivo" e quindi appaia all'inizio dell'elenco...
Comunque, forse un nuovo post con titolo adatto opera una migliore selezione dei "lettori". E' un caso di equlibrio "separating", indotto da un segnale veridico. Tanto per non dimanticarmi il mestiere
ciao
Benissimo caro Patrone
manteniamo dunque questo thread ‘in caldo’. Il trhead in questione scritto da ubermench [ https://www.matematicamente.it/f/viewtop ... highlight= ] iniziava testualmente così…
Sia $g$ una funzione continua e $y$ soluzione dell'equazione differenziale $y'=g(y)$. Mostrare che $y$ non ammette punti di minimo e/o massimo propri…
Diciamo che alla fine non si è riusciti a dare una risposta ben chiara e definita al quesito proposto, ma in compenso si è aperta la strada ad una serie di interessanti problemi. Per introdurre nuovamente l’argomento penso sia il caso di esaminare un problema, diciamo così, ‘concreto’. Nella località dove ho passato le vacanze era possibile acquistare [sia pure a prezzi non proprio ‘modici’ …] una grande varietà di orologi a cucù. Tra vari i tipi quello che ha ispirato in un certo senso la mia ‘fantasia’ è l’orologio qui sotto rappresentato…
A differenza del tipo ‘normale’, questo orologio a cucù utilizza come pendolo una ragazzotta che va su e giù sull’altalena. Un semplice modello matematico del meccanismo di temporizzazione del cucù è rappresentato qui sotto…
Indicata con $x$ la quota della chioma della ragazzotta e supponendo che per $x=0$ la forza di richiamo della molla sia uguale al peso della ragazzotta, l’equazione che governa il moto è data da…
$m*x’’=-k*x$ (1)
… ove $m$ è la massa della ragazzotta e $k$ il coefficiente di elasticità della molla. Per semplificare le cose supponiamo di scegliere un sistema metrico nel quale sia $m=k=1$, per cui sarà…
$x’’=-x$ (2)
L’equazione (1) pressuppone che l’energia del sistema sia costante per cui, nelle ipotesi fatte, la somma dell’energia potenziale e dell’energia cinetica è costante, ovvero è…
$E=1/2*x’^2+u(x)$ (3)
L’energia potenziale è espressa dalla relazione…
$u(x)=int_0^x alpha*dalpha= ½*x^2$ (4)
In definitiva dunque la (3) diviene…
$x’= sqrt(2*(e-u(x)))=sqrt (2*(E-1/2*x^2))$ (5)
Per risolvere la (5) occorre fornire la condizione iniziale, ossia mettere in moto il nostro cucù. Far questo è oltremodo semplice, basta tirare in basso in piedi della ragazzotta in modo da portarla alla quota $x=-1$ e all’istante $t=0$ lasciarla andare. La (4) ci dice che all’istante $t=0$ l’energia sarà tutta potenziale con valore $E=1/2$. Di conseguenza l’equazione del moto ‘su e giù’ della ragazzotta sarà…
$x’=sqrt(1-x^2)$ con $x(0)=-1$ (6)
Prima di procedere una considerazione importante. Per la natura del problema la funzione ‘radice quadrata’ che compare nella (6) è da intendersi a due valori, vale a dire per un certo valore di $x$ sono definiti due valori di $x’$, uguali in modulo ma di segno opposto…
Arrivati a questo punto mi par giusto sottoporre riguardo alla (6) le stesse identiche domande che ha posto Patrone, vale a dire…
- l’equazione ha una ed una sola soluzione [massimale]?…
- in caso di risposta affermativa alla precedente domanda, essa è definita su tutto $\RR$?…
- sempre se esiste una soluzione massimale, trovarne una espressione analitica
Buon lavoro ragazzi!… e naturalmente…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
manteniamo dunque questo thread ‘in caldo’. Il trhead in questione scritto da ubermench [ https://www.matematicamente.it/f/viewtop ... highlight= ] iniziava testualmente così…
Sia $g$ una funzione continua e $y$ soluzione dell'equazione differenziale $y'=g(y)$. Mostrare che $y$ non ammette punti di minimo e/o massimo propri…
Diciamo che alla fine non si è riusciti a dare una risposta ben chiara e definita al quesito proposto, ma in compenso si è aperta la strada ad una serie di interessanti problemi. Per introdurre nuovamente l’argomento penso sia il caso di esaminare un problema, diciamo così, ‘concreto’. Nella località dove ho passato le vacanze era possibile acquistare [sia pure a prezzi non proprio ‘modici’
…] una grande varietà di orologi a cucù. Tra vari i tipi quello che ha ispirato in un certo senso la mia ‘fantasia’ è l’orologio qui sotto rappresentato… A differenza del tipo ‘normale’, questo orologio a cucù utilizza come pendolo una ragazzotta che va su e giù sull’altalena. Un semplice modello matematico del meccanismo di temporizzazione del cucù è rappresentato qui sotto…
Indicata con $x$ la quota della chioma della ragazzotta e supponendo che per $x=0$ la forza di richiamo della molla sia uguale al peso della ragazzotta, l’equazione che governa il moto è data da…
$m*x’’=-k*x$ (1)
… ove $m$ è la massa della ragazzotta e $k$ il coefficiente di elasticità della molla. Per semplificare le cose supponiamo di scegliere un sistema metrico nel quale sia $m=k=1$, per cui sarà…
$x’’=-x$ (2)
L’equazione (1) pressuppone che l’energia del sistema sia costante per cui, nelle ipotesi fatte, la somma dell’energia potenziale e dell’energia cinetica è costante, ovvero è…
$E=1/2*x’^2+u(x)$ (3)
L’energia potenziale è espressa dalla relazione…
$u(x)=int_0^x alpha*dalpha= ½*x^2$ (4)
In definitiva dunque la (3) diviene…
$x’= sqrt(2*(e-u(x)))=sqrt (2*(E-1/2*x^2))$ (5)
Per risolvere la (5) occorre fornire la condizione iniziale, ossia mettere in moto il nostro cucù. Far questo è oltremodo semplice, basta tirare in basso in piedi della ragazzotta in modo da portarla alla quota $x=-1$ e all’istante $t=0$ lasciarla andare. La (4) ci dice che all’istante $t=0$ l’energia sarà tutta potenziale con valore $E=1/2$. Di conseguenza l’equazione del moto ‘su e giù’ della ragazzotta sarà…
$x’=sqrt(1-x^2)$ con $x(0)=-1$ (6)
Prima di procedere una considerazione importante. Per la natura del problema la funzione ‘radice quadrata’ che compare nella (6) è da intendersi a due valori, vale a dire per un certo valore di $x$ sono definiti due valori di $x’$, uguali in modulo ma di segno opposto…
Arrivati a questo punto mi par giusto sottoporre riguardo alla (6) le stesse identiche domande che ha posto Patrone, vale a dire…
- l’equazione ha una ed una sola soluzione [massimale]?…
- in caso di risposta affermativa alla precedente domanda, essa è definita su tutto $\RR$?…
- sempre se esiste una soluzione massimale, trovarne una espressione analitica
Buon lavoro ragazzi!… e naturalmente…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
Ragazzi
possibile che nessuno di voi voglia cimentarsi con il ‘problema del cucù’?… In fin dei conti si tratta della seguente ‘banale’ equazione differenziale del primo ordine nella variabile $t$…
$x’= sqrt(1-x^2)$ con $x(0)=-1$ (1)
Unica ‘difficoltà’ [se vogliamo definirla così…] è che, se scriviamo la (1) come $x’=f(x)$ e cerchiamo una soluzione in cui la ragazzotta vada ‘su è giù’, dobbiamo per forza ipotizzare che la $f(x)$ sia a più valori, vale a dire per ogni $x$ essa abbia sia un valore positivo sia un valore negativo. Seguendo poi i suggerimenti di Luca proviamo magari a rispondere alla prima delle domande, vale a dire: il problema (1) ammette una e una sola soluzione?…
Se la cosa può agevolarvi vi mostro il grafico della funzione $f(x)=sqrt(1-x^2)$ che compare nella (1)…
In effetti la funzione sudetta è rappresentata da un cerchio e mi ricorda il tempo in cui, per verificare la quadratura di una coppia di segnali, la riproducevo sull’oscillografo. Se i due segnali [isofrequenziali ovviamente…] erano in perfetta quadratura tra loro appariva un cerchio, diversamente una ellisse più o meno ‘storta’. Ricordo bene che ad occhio riuscivo a diagnosticare errori di fase anche inferiori ad un grado… altri tempi ragazzi!…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
possibile che nessuno di voi voglia cimentarsi con il ‘problema del cucù’?… In fin dei conti si tratta della seguente ‘banale’ equazione differenziale del primo ordine nella variabile $t$…
$x’= sqrt(1-x^2)$ con $x(0)=-1$ (1)
Unica ‘difficoltà’ [se vogliamo definirla così…] è che, se scriviamo la (1) come $x’=f(x)$ e cerchiamo una soluzione in cui la ragazzotta vada ‘su è giù’, dobbiamo per forza ipotizzare che la $f(x)$ sia a più valori, vale a dire per ogni $x$ essa abbia sia un valore positivo sia un valore negativo. Seguendo poi i suggerimenti di Luca proviamo magari a rispondere alla prima delle domande, vale a dire: il problema (1) ammette una e una sola soluzione?…
Se la cosa può agevolarvi vi mostro il grafico della funzione $f(x)=sqrt(1-x^2)$ che compare nella (1)…
In effetti la funzione sudetta è rappresentata da un cerchio e mi ricorda il tempo in cui, per verificare la quadratura di una coppia di segnali, la riproducevo sull’oscillografo. Se i due segnali [isofrequenziali ovviamente…] erano in perfetta quadratura tra loro appariva un cerchio, diversamente una ellisse più o meno ‘storta’. Ricordo bene che ad occhio riuscivo a diagnosticare errori di fase anche inferiori ad un grado… altri tempi ragazzi!…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
Effettivamente il problema mi interessa... mi interessa soprattutto per vedere dove sta il tranello 
L'equazione differenziale $x'=sqrt(1-x^2)$ con $x(0)=-1$ ammette come soluzione $x(t)=-cost$ oppure si potrebbe scrivere $x(t)=sin(t-pi/2)$ o ancora $x(t)=sin(t+3/2pi)$ ma è la stessa cosa. Sull'insieme di definzione non sono molto sicuro. Per trovare il risultato ho dovuto integrare un'espressione e invertire la funzioni $arc cos$, che non è definita su tutto $RR$, il cui codominio è $(0,pi)$ dunque il dominio della soluzione dovrebbe essere $(0,pi)$. Ora si chiede se sia possibile estendere tale soluzione con una che abbia un dominio più esteso?
Parola a lupo grigio per qualche delucidazione
L'equazione differenziale $x'=sqrt(1-x^2)$ con $x(0)=-1$ ammette come soluzione $x(t)=-cost$ oppure si potrebbe scrivere $x(t)=sin(t-pi/2)$ o ancora $x(t)=sin(t+3/2pi)$ ma è la stessa cosa. Sull'insieme di definzione non sono molto sicuro. Per trovare il risultato ho dovuto integrare un'espressione e invertire la funzioni $arc cos$, che non è definita su tutto $RR$, il cui codominio è $(0,pi)$ dunque il dominio della soluzione dovrebbe essere $(0,pi)$. Ora si chiede se sia possibile estendere tale soluzione con una che abbia un dominio più esteso?
Parola a lupo grigio per qualche delucidazione
Complimenti a Kroldar per avere ‘rotto il ghiaccio’!…
A prima vista la ‘soluzione’ da lui trovata [$x= -cos t$] risolve il problema di Cauchy…
$x’=sqrt(1-x^2)$
$x(0)=-1$ (1)
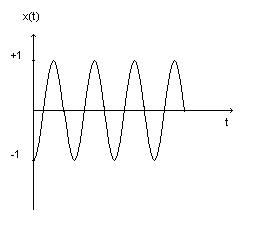
Del resto anche il buon senso ci suggerisce che la ‘ragazzotta del cucù’, una volta lasciata libera l’altalena, si metterà ad andare ‘su e giù’. Sfortunatamente però non sempre la matematica ed il buon senso vanno d’accordo e già qualcuno [qualcuno di nostra conoscenza…] potrebbe fare l’obiezione seguente…
perché la soluzione data sia valida è necessario che la funzione radice quadrata che compare nelle (1) assuma sia i valori positivi sia i valori negativi, ovvero sia ‘polidroma’ e questa classe di funzioni è stato detto più volte che non esistono… o per lo meno non sono funzioni…
A costui come si può rispondere?…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
A prima vista la ‘soluzione’ da lui trovata [$x= -cos t$] risolve il problema di Cauchy…
$x’=sqrt(1-x^2)$
$x(0)=-1$ (1)
Del resto anche il buon senso ci suggerisce che la ‘ragazzotta del cucù’, una volta lasciata libera l’altalena, si metterà ad andare ‘su e giù’. Sfortunatamente però non sempre la matematica ed il buon senso vanno d’accordo e già qualcuno [qualcuno di nostra conoscenza…] potrebbe fare l’obiezione seguente…
perché la soluzione data sia valida è necessario che la funzione radice quadrata che compare nelle (1) assuma sia i valori positivi sia i valori negativi, ovvero sia ‘polidroma’ e questa classe di funzioni è stato detto più volte che non esistono… o per lo meno non sono funzioni…
A costui come si può rispondere?…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
"lupo grigio":
perché la soluzione data sia valida è necessario che la funzione radice quadrata che compare nelle (1) assuma sia i valori positivi sia i valori negativi, ovvero sia ‘polidroma’ e questa classe di funzioni è stato detto più volte che non esistono… o per lo meno non sono funzioni…
Perché? la soluzione da me fornita non necessita di polidromia. La derivata di $-cost$ è $sint$, che nell'intervallo $(0,pi)$ è sempre positiva... non capisco
Secondo me non c'è nessun fatto strano derivante da queste equazioni:
Se vuoi una espressione della posizione in funzione del tempo:
${(\ddot{x}+x=0),(x(0)=-1),(\dot{x}(0)=0):}=>x(t)=-\cost=>\dot{x}(t)=\sint$ In questo caso si vede bene come la velocità sia positiva o negativa ogni mezzo periodo o oscillazione...
Il problema invece nasce se vuoi una espressione del tipo: $\dot{x}(x)$ in quanto non la puoi ottenere in forma vettoriale, ma ottieni al max $||\dot{x}(x)||$.
Infatti:
$\int_0^{v(x)}vdv=-\int_-1^x\phid\phi=>v^2(x)/2=(1-x^2)/2=>v^2(x)=(1-x^2)=\vec{v(x)}\cdot\vec{v(x)}=||\vec{v(x)}||^2$
Quindi:
$||\vec{v(x)}||=\sqrt{1-x^2}$ $: x\in[-1,1]$
Come vedi non ci sono contraddizioni...
Se ho ben capito quello che dicevi...
Se vuoi una espressione della posizione in funzione del tempo:
${(\ddot{x}+x=0),(x(0)=-1),(\dot{x}(0)=0):}=>x(t)=-\cost=>\dot{x}(t)=\sint$ In questo caso si vede bene come la velocità sia positiva o negativa ogni mezzo periodo o oscillazione...
Il problema invece nasce se vuoi una espressione del tipo: $\dot{x}(x)$ in quanto non la puoi ottenere in forma vettoriale, ma ottieni al max $||\dot{x}(x)||$.
Infatti:
$\int_0^{v(x)}vdv=-\int_-1^x\phid\phi=>v^2(x)/2=(1-x^2)/2=>v^2(x)=(1-x^2)=\vec{v(x)}\cdot\vec{v(x)}=||\vec{v(x)}||^2$
Quindi:
$||\vec{v(x)}||=\sqrt{1-x^2}$ $: x\in[-1,1]$
Come vedi non ci sono contraddizioni...
Se ho ben capito quello che dicevi...
Molto bene ragazzi
vedo che l'argomento interessa. La 'obiezione' sollevata da C.P.S. è esatta e occorre subito che dica che se avessi impostato il 'problema del cucù' il maniera 'standard' [ vale a dire $x''=-x$, $x(0)=-1$,$x'(0)=0$...] esso non avrebbe presentato difficoltà di sorta. Come è stato invece impostato da me porta ad una equazione differenziale in apparenza 'semplice', in realtà un vero e proprio 'campo minato'... il tutto coscientemente 
...
Per renderci conto di questo vediamo ora l'altra 'obiezione', quella di Kroldar...
... la soluzione da me fornita non necessita di polidromia... la derivata di $-cost$ è $sint$, che nell'intervallo $(0,pi)$ è sempre positiva...
La prima osservazione che occorre fare è che nel problema da me posto non si accennava al dominio e codominio della $x(t)$. Osservando l'equazione...
$x'=sqrt(1-x^2)$ (1)
... ci si rende immediatamente conto che deve essere $-1<=x<=1$ e pertanto, almeno per la $x$ il campo di esistenza è implicitamente definito. Per quanto riguarda la variabile $t$ se esso non è definito si deve intendere l'intero insieme $RR$ o quanto meno, dal momento che è data la condizione per $t=0$, l'insieme $RR^+$. La soluzione fornita da Kroldar è limitata all'intervallo $(0,pi)$... ok!, per il momento accettiamo questo...
La soluzione di Kroldar è $x(t)= -cos t$ ed effettivamente soddisfa la (1) in quanto è vero che...
$x'(t)= sin t= sqrt(1-cos^2 t)$ (2)
... ed è vero altresì che in $(0,pi)$ è $sin t>=0$. A questo punto però proviamo una versione del 'problema del cucù' un poco modificata e supponiamo di avviare l'orologio non tirando giù la ragazzotta, bensì sollevandola fino a $x=1$ per poi lasciarla andare all'istante $t=0$. Il problema di Cauchy diviene ora il seguente...
$x'=sqrt(1-x^2)$
$x(0)=1$ (1)
Procedendo allo stesso modo di Kroldar si trova che la soluzione è $x(t)=cos t$ con $t$ in $(0,pi)$. Anche questa funzione soddisfa la (1) in quanto è...
$x'(t)=-sin t= sqrt(1-cos^2 t)$ (4)
A differenza di prima però in $(0,pi)$ è $-sin t<=0$, vale a dire è $x'(t)<0$. In entrambi i casi la (1) è soddisfatta, solo che nel primo caso occorre scegliere il 'valore positivo' della funzione 'radice quadrata', nel secondo caso il 'valore negativo'. Dal momento che in entrambi i casi la soluzione fornita è valida, occorre di forza accettare il fatto che la funzione $f(x)=sqrt(1-x^2)$ che compare nella (1) è 'a due valori'...
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
vedo che l'argomento interessa. La 'obiezione' sollevata da C.P.S. è esatta e occorre subito che dica che se avessi impostato il 'problema del cucù' il maniera 'standard' [ vale a dire $x''=-x$, $x(0)=-1$,$x'(0)=0$...] esso non avrebbe presentato difficoltà di sorta. Come è stato invece impostato da me porta ad una equazione differenziale in apparenza 'semplice', in realtà un vero e proprio 'campo minato'... il tutto coscientemente
... Per renderci conto di questo vediamo ora l'altra 'obiezione', quella di Kroldar...
... la soluzione da me fornita non necessita di polidromia... la derivata di $-cost$ è $sint$, che nell'intervallo $(0,pi)$ è sempre positiva...
La prima osservazione che occorre fare è che nel problema da me posto non si accennava al dominio e codominio della $x(t)$. Osservando l'equazione...
$x'=sqrt(1-x^2)$ (1)
... ci si rende immediatamente conto che deve essere $-1<=x<=1$ e pertanto, almeno per la $x$ il campo di esistenza è implicitamente definito. Per quanto riguarda la variabile $t$ se esso non è definito si deve intendere l'intero insieme $RR$ o quanto meno, dal momento che è data la condizione per $t=0$, l'insieme $RR^+$. La soluzione fornita da Kroldar è limitata all'intervallo $(0,pi)$... ok!, per il momento accettiamo questo...
La soluzione di Kroldar è $x(t)= -cos t$ ed effettivamente soddisfa la (1) in quanto è vero che...
$x'(t)= sin t= sqrt(1-cos^2 t)$ (2)
... ed è vero altresì che in $(0,pi)$ è $sin t>=0$. A questo punto però proviamo una versione del 'problema del cucù' un poco modificata e supponiamo di avviare l'orologio non tirando giù la ragazzotta, bensì sollevandola fino a $x=1$ per poi lasciarla andare all'istante $t=0$. Il problema di Cauchy diviene ora il seguente...
$x'=sqrt(1-x^2)$
$x(0)=1$ (1)
Procedendo allo stesso modo di Kroldar si trova che la soluzione è $x(t)=cos t$ con $t$ in $(0,pi)$. Anche questa funzione soddisfa la (1) in quanto è...
$x'(t)=-sin t= sqrt(1-cos^2 t)$ (4)
A differenza di prima però in $(0,pi)$ è $-sin t<=0$, vale a dire è $x'(t)<0$. In entrambi i casi la (1) è soddisfatta, solo che nel primo caso occorre scegliere il 'valore positivo' della funzione 'radice quadrata', nel secondo caso il 'valore negativo'. Dal momento che in entrambi i casi la soluzione fornita è valida, occorre di forza accettare il fatto che la funzione $f(x)=sqrt(1-x^2)$ che compare nella (1) è 'a due valori'...
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo