Parametrizzazione
Salve voglio trovare le equazioni parametriche di una semisfera di raggio $R$ allora so che l' equazione di una sfera è uguale a $x^2+y^2+z^2=R^2$ l' equazione della semisfera la possiamo scrivere in questo modo $z=sqrt(R^2-x^2-y^2)$ ma adesso come parametrizzare in coordinate polari???
Risposte
Dividendo l'equazione della sfera per \(R^2\) ottieni:
\[
\left( \frac{x}{R}\right)^2 +\left( \frac{y}{R}\right)^2+\left( \frac{z}{R}\right)^2=1\; ;
\]
dato che la somma dei primi due addendi è nonnegativa, la puoi chiamare \(A^2(x,y)\): fatto ciò, la relazione:
\[
A^2(x,y) + \left( \frac{z}{R}\right)^2 =1
\]
è praticamente uguale alla relazione fondamentale della trigonometria; perciò puoi dire che, per ogni valore di \((x,y,z)\in S(0;R)\) esiste un \(\theta \in \mathbb{R}\) tale che:
\[
\left( \frac{z}{R}\right)^2 = \cos^2 \theta \qquad \text{e} \qquad A^2(x,y)=\sin^2 \theta\; ;
\]
supponendo \(\sin \theta >0\), si possono dividere ambo i membri della seconda equazione per \(\sin^2 \theta\) ottenendo:
\[
\left( \frac{x}{R\sin \theta}\right)^2 +\left( \frac{y}{R\sin \theta}\right)^2 =1\; ,
\]
ed usando di nuovo la relazione fondamentale si trova:
\[
\left( \frac{x}{R\sin \theta}\right)^2 = \cos^2 \phi \qquad \text{e} \qquad \left( \frac{y}{R\sin \theta}\right)^2 =\sin^2 \phi\; .
\]
Esplicitando con un po' di attenzione le tre equazioni rispetto ad \(x,y,z\) si trova:
\[
\begin{cases}
x=R\ \cos \phi\ \sin \theta\\
y=R\ \sin \phi\ \sin \theta\\
z=R\ \cos \theta
\end{cases}
\]
che è la parametrizzazione in polari.
Ovviamente si possono usare argomenti di tipo geometrico, ma questo è fatto su ogni buon testo di Analisi II pre-riforma.
\[
\left( \frac{x}{R}\right)^2 +\left( \frac{y}{R}\right)^2+\left( \frac{z}{R}\right)^2=1\; ;
\]
dato che la somma dei primi due addendi è nonnegativa, la puoi chiamare \(A^2(x,y)\): fatto ciò, la relazione:
\[
A^2(x,y) + \left( \frac{z}{R}\right)^2 =1
\]
è praticamente uguale alla relazione fondamentale della trigonometria; perciò puoi dire che, per ogni valore di \((x,y,z)\in S(0;R)\) esiste un \(\theta \in \mathbb{R}\) tale che:
\[
\left( \frac{z}{R}\right)^2 = \cos^2 \theta \qquad \text{e} \qquad A^2(x,y)=\sin^2 \theta\; ;
\]
supponendo \(\sin \theta >0\), si possono dividere ambo i membri della seconda equazione per \(\sin^2 \theta\) ottenendo:
\[
\left( \frac{x}{R\sin \theta}\right)^2 +\left( \frac{y}{R\sin \theta}\right)^2 =1\; ,
\]
ed usando di nuovo la relazione fondamentale si trova:
\[
\left( \frac{x}{R\sin \theta}\right)^2 = \cos^2 \phi \qquad \text{e} \qquad \left( \frac{y}{R\sin \theta}\right)^2 =\sin^2 \phi\; .
\]
Esplicitando con un po' di attenzione le tre equazioni rispetto ad \(x,y,z\) si trova:
\[
\begin{cases}
x=R\ \cos \phi\ \sin \theta\\
y=R\ \sin \phi\ \sin \theta\\
z=R\ \cos \theta
\end{cases}
\]
che è la parametrizzazione in polari.
Ovviamente si possono usare argomenti di tipo geometrico, ma questo è fatto su ogni buon testo di Analisi II pre-riforma.
"gugo82":
Esplicitando con un po' di attenzione le tre equazioni rispetto ad \(x,y,z\) si trova:
\[
\begin{cases}
x=R\ \cos \phi\ \sin \theta\\
y=R\ \sin \phi\ \sin \theta\\
z=R\ \cos \theta
\end{cases}
\]
che è la parametrizzazione in polari.
quindi questa è la parametrizzazione di una semisfera, giusto???? Se ne voglio calcolare l' integrale di superficie $int_S x^2dS$ con $R=1$ quale diventa il mio dominio di integrazione????
La parametrizzazione che ti ho indicato copre l'intera sfera, se prendi \((\theta ,\phi)\in [0,\pi]\times [0,2\pi]\).
scusami io voglio trovare la parametrizzazione di una semisfera, come posso fare??? insomma della metà superiore
Quale semisfera?
Quella nel semipiano \(z>0\)?
Se sì, basta prendere \(\theta \in [0,\pi/2]\) e \(\phi \in [0,2\pi]\).
Quella nel semipiano \(z>0\)?
Se sì, basta prendere \(\theta \in [0,\pi/2]\) e \(\phi \in [0,2\pi]\).
Quindi la parametrizzazione che mi hai fatto vedere va bene anche per la semisfera (a me sembra più la parametrizzazione di una sfera)??
Se hai capito come funziona la parametrizzazione in coordinate polari, in particolare cosa rappresentano i valori \(\theta\) e \(\phi\), allora non dovresti trovare difficoltà a visualizzare che succede quando \((\theta, \phi) \in [0,\pi/2]\times [0,2\pi]\).
Se non riesci a visualizzare la cosa, questa figura:
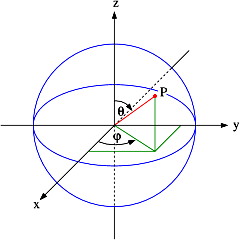
può essere utile.
Se non riesci a visualizzare la cosa, questa figura:

può essere utile.
ma se di una superficie voglio calcolarne la normale cosa devo fare???? devo fare il prodotto vettoriale di cosa???
Per definizione, se la superficie è data in forma parametrica $r(u,v)=(x(u,v),y(u,v),z(u,v))$, detti $r_u,\ r_v$ i generatori del piano tangente, la normale (vettore) è data da $N=r_u \times r_v$. Ma dovresti saperle queste cose dalla teoria, no?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo