Lipschitzianità di una funzione
Volevo chiedere qualche chiarimento su come dedurre che una funzione sia lispchitziana su un certo dominio? E come uniformemente continua? Tenendo conto del teorema di Cantor-Heine e del fatto che se una funzione è lipschitziana è uniformemente continua, una funzione di questo tipo ad esempio:
$f(x)={((x^2+5x+6)/|x-1|,if x<=0),(x+6-(x+1)log(x+1),if x>0):}$
come fareste a dire se è lipschitziana e/o uniformemente continua? Considerando che la funzione è continua in $x=0$, ha un asintoto obliquo per $x->-oo$ e diverge a $-oo$ per $x->+oo$, io ma senza ancora capire bene come, direi che è lipschitziana su $(-oo,a]$ con $a>0$ ma con $a!=+oo$ poichè la derivata si mantiene limitata in questo insieme e vi è addirittura un asintoto obliquo per $x$ che diverge negativamente. Potreste darmi qualche delucidazione?
$f(x)={((x^2+5x+6)/|x-1|,if x<=0),(x+6-(x+1)log(x+1),if x>0):}$
come fareste a dire se è lipschitziana e/o uniformemente continua? Considerando che la funzione è continua in $x=0$, ha un asintoto obliquo per $x->-oo$ e diverge a $-oo$ per $x->+oo$, io ma senza ancora capire bene come, direi che è lipschitziana su $(-oo,a]$ con $a>0$ ma con $a!=+oo$ poichè la derivata si mantiene limitata in questo insieme e vi è addirittura un asintoto obliquo per $x$ che diverge negativamente. Potreste darmi qualche delucidazione?
Risposte
Intendevo la derivata prima (che presenta al denominatore $ 2*sqrt(|x|) $
Infatti la derivata prima non esiste proprio per $x=0$. Ma questo non è sufficiente a dire che una funzione non è Lipschitziana. Invece è sufficiente verificare che la derivata prima non è limitata. Come faresti?
Vedo che in x=0 la derivata ha un asintoto verticale. Giusto?
Ok.
Riformulo quanto detto prima: una funzione è lipschitziana in un intervallo (a,b) se:
- la sua derivata è continua in (a,b)
- la sua derivata non presenta asintoti verticali in (a,b)
- la sua derivata non diverge agli estremi dell'intervallo (a,b) (=> ha asintoto obliquo od orizzontale)
Mi pare non manchi nulla...
- la sua derivata è continua in (a,b)
- la sua derivata non presenta asintoti verticali in (a,b)
- la sua derivata non diverge agli estremi dell'intervallo (a,b) (=> ha asintoto obliquo od orizzontale)
Mi pare non manchi nulla...
Si, operativamente quella tabellina funziona nel 90% dei casi. Ma non è corretta. L'enunciato corretto è:
una funzione $f:I \to RR$ derivabile è Lipschitziana se e solo se $f'$ è limitata in $I$.
Fine. Di meglio non si può fare. Ad esempio, la funzione
[tex]$F(x)=\int_0^x t\sin(t)\,\mathrm{d}t,\quad x \in \mathbb{R}[/tex]
verifica le tue ipotesi, ma non è Lipschitziana. Guarda infatti il grafico della sua derivata:
[asvg]xmin=-15*Math.PI; xmax=15*Math.PI;axes(); plot("x*sin(x)");[/asvg]
Vedi che non è limitata? Eppure non ha asintoti verticali, e nemmeno diverge agli estremi dell'intervallo.
una funzione $f:I \to RR$ derivabile è Lipschitziana se e solo se $f'$ è limitata in $I$.
Fine. Di meglio non si può fare. Ad esempio, la funzione
[tex]$F(x)=\int_0^x t\sin(t)\,\mathrm{d}t,\quad x \in \mathbb{R}[/tex]
verifica le tue ipotesi, ma non è Lipschitziana. Guarda infatti il grafico della sua derivata:
[asvg]xmin=-15*Math.PI; xmax=15*Math.PI;axes(); plot("x*sin(x)");[/asvg]
Vedi che non è limitata? Eppure non ha asintoti verticali, e nemmeno diverge agli estremi dell'intervallo.
La funzione che hai riportato non è Lipschitziana su R, e fin qui ci sono. Mi verrebbe però da aggiungere che è LOCALMENTE Lipschitziana, dico bene?
PS: mutuo il discorso sulla Lipschitziana locale dal fatto che $ x^2 $ non lo è su R ma lo è localmente.
PS: mutuo il discorso sulla Lipschitziana locale dal fatto che $ x^2 $ non lo è su R ma lo è localmente.
Si, certo. Perché su ogni sottoinsieme compatto di $RR$ la derivata prima è limitata. Niente di particolarmente strano, questo è vero per ogni funzione derivabile con derivata continua.
"dissonance":
è vero per ogni funzione derivabile con derivata continua.
Proprio quello che pensavo (e speravo) di sentirmi dire
Credo proprio di aver capito, o quantomeno di essermi tolto un bel pò di dubbi; grazie a quanti sono intervenuti, ed in particolare a dissonance per la pazienza
Riuppo il topic per fare una domanda.
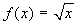con I= [0, +∞[ è uniformemente continua?
con I= [0, +∞[ è uniformemente continua?
Sì.
Infatti si ha:
\[
|\sqrt{x}-\sqrt{y}| \leq \sqrt{|x-y|}
\]
e da qui concludi.
Infatti si ha:
\[
|\sqrt{x}-\sqrt{y}| \leq \sqrt{|x-y|}
\]
e da qui concludi.
Scusami ma non capisco.
Faccio un esempio. Se io ho la funzione f(x)= x^2, non riesco a trovare un δ affinchè sia vera la definizione di continuità uniforme. Ma non dovrebbe essere la stessa cosa con radice di x? Sto sbagliando qualcosa di estremamente stupido ma non riesco a capire...
Faccio un esempio. Se io ho la funzione f(x)= x^2, non riesco a trovare un δ affinchè sia vera la definizione di continuità uniforme. Ma non dovrebbe essere la stessa cosa con radice di x? Sto sbagliando qualcosa di estremamente stupido ma non riesco a capire...
No, non è la stessa cosa.
Infatti la funzione \(x^2\) non è uniformemente continua in \([0,\infty[\), mentre \(\sqrt{x}\) lo è per la disuguaglianza precedente.
Il problema con \(x^2\) è che essa cresce troppo velocemente e perciò non soddisfa il teorema della farfalla.
Infatti la funzione \(x^2\) non è uniformemente continua in \([0,\infty[\), mentre \(\sqrt{x}\) lo è per la disuguaglianza precedente.
Il problema con \(x^2\) è che essa cresce troppo velocemente e perciò non soddisfa il teorema della farfalla.
Quindi radice di x è uniformemente continua perchè tende a 0 troppo lentamente?
"Asynth":
Quindi radice di x è uniformemente continua perchè tende a 0 troppo lentamente?
No.
La funzione \(\sqrt{x}\) è uniformemente continua perché vale la disuguaglianza già citata sopra, cioè:
"gugo82":
\[
|\sqrt{x}-\sqrt{y}| \leq \sqrt{|x-y|}
\]
Tale disuguaglianza si esprime anche dicendo che \(\sqrt{x}\) è una funzione Hölderiana d'esponente \(1/2\).
P.S.: Ti prego di notare che il teorema della farfalla è solo una condizione necessaria all'uniforme continuità in intervalli non limitati.
Grazie mille 
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo