Limite esponenziale
eccoti il limite ubermensch, purtroppo non ho trovato proprio quello che dicevo io, cmq ti posto questo che è molto simile a quello che avevo visto io:
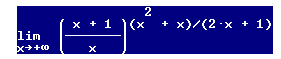
io ho cercato di ricondurlo ad una cosa del tipo e elevato alla frazione che sta all'esponente che moltiplica il log di ( x+1 )/x solo che poi non sapevo come procedere, il log si può far diventare 0 se si raccoglie per x e la si semplifica, ma poi rimane sempre la x^2 della frazione che lo moltiplica, che anke se si semplifica con la x del denominatore rimane sempre presente come primo grado...
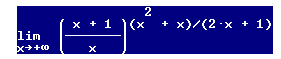
io ho cercato di ricondurlo ad una cosa del tipo e elevato alla frazione che sta all'esponente che moltiplica il log di ( x+1 )/x solo che poi non sapevo come procedere, il log si può far diventare 0 se si raccoglie per x e la si semplifica, ma poi rimane sempre la x^2 della frazione che lo moltiplica, che anke se si semplifica con la x del denominatore rimane sempre presente come primo grado...
Risposte
L'esponenete si può riscrivere come:
esp = (1/2)x + (1/4) - (1/4)/(2x+1)
Chiamo A=(1/2)x, B=1/4, C=-(1/4)/(2x+1)
la base si può scrivere:
base = 1 + 1/x
Dunque:
base^A --> sqrt(e)
base^B --> 1
base^C --> 1
Facendo il prodotto si vede che il limite è sqrt(e)
esp = (1/2)x + (1/4) - (1/4)/(2x+1)
Chiamo A=(1/2)x, B=1/4, C=-(1/4)/(2x+1)
la base si può scrivere:
base = 1 + 1/x
Dunque:
base^A --> sqrt(e)
base^B --> 1
base^C --> 1
Facendo il prodotto si vede che il limite è sqrt(e)
mi hai fregato goblyn
comunque concordo: viene anche a me così e conferma anche il signor Derive.
ciao, ubermensch
comunque concordo: viene anche a me così e conferma anche il signor Derive.
ciao, ubermensch
ora mi guardo il procedimento e vedo di capirlo bene, grazie per l'aiuto 

scusate la mia ignoranza ragazzi  come fate a cambiare la frazione che sta all'esponente in questo modo : esp = (1/2)x + (1/4) - (1/4)/(2x+1) ? per la base tutto ok... ma non capisce la modifica dell'esponente...
come fate a cambiare la frazione che sta all'esponente in questo modo : esp = (1/2)x + (1/4) - (1/4)/(2x+1) ? per la base tutto ok... ma non capisce la modifica dell'esponente...
ho fatto la divisione tra numeratore e denominatore col procedimento classico di divisione tra polinomi. In alternativa puoi usare anche ruffini visto che il den è di primo grado!
ah ok grazie goblyn...non me ne ero proprio accorto !!!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo